The concept of BE-algebras has been propounded and extensively studied by Kim and Kim (2006). The class of BE-algebras has been introduced as a generalization of the class of BCK-algebras of Iseki and Tanaka (1979). Some properties of filters of BE-algebras were studied by Ahn et al. (2012) and by Meng (2010). The notion of dual ideals in BCK-algebras has been introduced by Deeba (1979). Meng (1996) introduced the notion of BCK-filters in BCK-algebras and presented a description of the BCK-filter generated by a set. In this paper, he discussed prime and irreducible decompositions. Jun et al. (1998) considered the fuzzification of the concept of BCK-filters, and investigated their properties. Later Sun (2000) explored the homomorphism theorems via dual ideals in bounded BCK-algebras. Walendziak (2008) discussed some properties of commutative BE-algebras. He also discovered the relationship between BE-algebras, implicative algebras and J-algebras. Çiloğlu and Çeven (2013) introduced the notion of bounded BE-algebras and researched some properties of them. Paad (2017) introduced the notion of radical of ideals in BL-algebras and then characterized the notion of the radical of ideals by elements of a BL-algebra.

In this work, the notion of semi-simple BE-algebras is introduced and its properties have been studied. The concept of radicals of ideals is introduced in bounded BE-algebras. The elements of a radicals of ideals are characterized in selfdistributive BE-algebras. Certain properties of these radicals are then derived with respect to set-intersection, direct products and homomorphic images.

The notion of semi-maximal ideals is introduced in bounded BE-algebras in terms of radicals of ideals. Some equivalent conditions are derived for every semi-maximal ideal of a BE-algebra to become a maximal ideal. Significant properties of semi-maximal ideals are derived with respect to homomorphisms, cartesian products and congruences.

In this section, we present certain definitions and results which are taken mostly from the papers (Ahn et al., 2012; Borzooei et al., 2014; Çiloğlu & Çeven, 2013; Kim & Kim, 2006; Meng, 2010; Prabhakar et al., 2019; Rao, 2015) for the ready reference of the reader.

Definition 1.1 Kim and Kim (2006): An algebra (X, *, 1) of type (2, 0) is called a BE-algebra if it satisfies the following properties:

A BE-algebra X is called self-distributive if x*(y*z) = ( x*y)(x *z) for all x, y, z ϵ X. A BE-algebra X is called transitive if y*z ( *y) ( *z) for all , y, z X. Every self-distributive BE-algebra is transitive. We introduce a relation on a BE-algebra X by y if and only if *y = 1 for all , y X. Clearly is reflexive.

Theorem 1.2 Meng, 2010: Let X be a transitive BE-algebra and x, y, z ϵ X. Then,

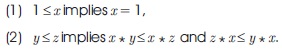
Definition 1.3 Kim and Kim (2006): A non-empty subset of a BE-algebra X is called a filter of X if, for all x, y ϵ X, it satisfies the following properties:

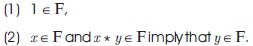
We denote by F(X) the set of all filters of F.

Theorem 1.4 Kim and Kim (2006): Let be a filter of a BE-algebra X. Then x ϵ F, x ≤ y imply that y ϵ F:

A filter of a BE-algebra X is called proper if X. A proper filter M of a BE-algebra is called maximal if there exists no proper filter Q of X such that M Q. For any a X, áañ = { X÷ an * = 1 for some n ℕ} is called the principal filter generated a (Ahn et al., 2012). If X is selfdistributive, then áañ = { X÷ a * = 1}. Theorem 1.5 Rao (2015): A proper filter M of a transitive BE-algebra X is maximal if and only if for each M, áM {x}ñ = X. A BE-algebra X is called bounded (Çiloğlu & Çeven, 2013) if there exists an element 0 satisfying 0 (or 0 * = 1) for all X. Define an unary operation N on a bounded BE-algebra X by N = * 0 for all X. Clearly 1N = 0 and 0N = 1. Borzooei et al. (2014) says clearly ker(f) = { X÷ f ( ) = 1} is a filter of X. Moreover, the set Dker(f) = { X÷ f ( ) = 0} is called dual kernel of the BE-homomorphism f. It is easy to check that Dker(f) = {0} whenever f is an injective homomorphism. Prabhakar et al. (2019) explained that an element of a bounded BE-algebra X is called dense if N = 0. We denote the set of all dense elements of a BE-algebra X by (X). Lemma 1.6: Let X be a transitive BE-algebra . For any , y, z X, we have,

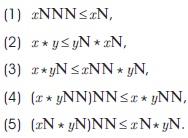
Lemma 1.7: Let X be a transitive BE-algebra X. For any , y, z X, we have,

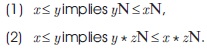
Definition 1.8: A non-empty subset I of a BE-algebra X is called an ideal of X if it satisfies the following conditions for all x, y

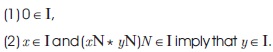
We denote by (X) the set of all ideals of a BE-algebra X. Here after, by a BE-algebra X we mean a bounded BE-algebra (X,*, 0, 1) unless otherwise mentioned. Proposition 1.9: Let I be an ideal of a transitive BE-algebra X. Then we have,

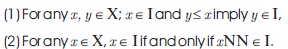
Theorem 1.10: Let X be a transitive BE-algebra and A X. Then,

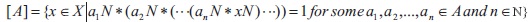
For A = {a}, we then denote [{a}], briefly by [a]. We call this ideal by principal ideal generated by a and is represented by [a] n = {x X÷ (aN) * xN = 1 for some n ℕ }. If X is self-distributive and a X, then [a] = {x X÷ aN * xN = 1}. Proposition 1.11: Let I is an ideal of a transitive BE-algebra X and A X. Then,

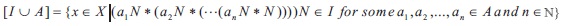
Corollary 1.12: Let X be a transitive BE-algebra and I is an ideal of X. For any

A proper ideal M of a BE-algebra X is said to be maximal (Borzooei et al., 2014); if M is not properly contained in any other proper ideal of X (i.e., M I X implies M = I or I = X for any ideal I of X).

Theorem 1.13: A proper ideal M of a transitive BE-algebra X is maximal if and only if [M {x}] = X for any

In this section, we introduce the concept of radical of a BE-algebra X. The notion of semi-simple BE-algebra is introduced and its properties are studied. The concept of radicals of ideals is introduced in BE-algebras. Certain properties of these radicals are then derived with respect to set-intersection, direct products and homomorphic images.

Theorem 2.1: Let X be a BE-algebra and I is an ideal of X. Then,

(1) I is proper if and only if 1ϵ I.

(2) Each proper ideal is contained in a maximal ideal.

Proof: (1) Assume that I is proper. Then I X. Suppose 1 I. For x X, we have (1N * xN)N = 1N = 0 I. Since 1 I and I is an ideal, we get x I. Hence X I. Thus I = X, which is a contradiction. The converse is clear.

(2) By the Zorn's lemma, it follows immediately.

Theorem 2.2: Every BE-algebra contains at least one maximal ideal.

Proof: Since {0} is a proper ideal of X, it is clear by above theorem 2.1.

Proposition 2.3: Let I be a proper ideal of a self-distributive BE-algebra X. Then I is maximal if and only if for any x ϵ X,

Proof: Let I be a proper ideal of X. Assume that I is maximal. Let x I. Then by Theorem 1.13, we get [I {x}] = X. Hence 1 [I {x}]. Since X is self-distributive, we get xNNN = (xN * 1N)N I. Since xN xNNN I. Then by Proposition 1.9 (1), we get xN I.

Conversely, assume the condition. Suppose I is not maximal. Then there exists a proper ideal Q of X such that I Q. Choose x Q - I. Then x I. By the assumed condition, we get xN I Q. Since xNNN xN, we get (xN * 1N)N = xNNN Q. Since x Q and Q is an ideal, we get 1 Q which is contradiction to that Q is proper. Therefore I is a maximal ideal of X. Definition 2.4: Let X be a BE-algebra and F is any subset of X.

Then the set (F) is defined as (F) = {x X÷ xN F}.

Proposition 2.5: The following implications hold in a BE-algebra X:

Proof: It is clearly proved by definition 2.4.

Proposition 2.6: Let X be a self-distributive BE-algebra. Then for any maximal filter F of X, (F) is a maximal ideal of X.

Proof: Let F be a maximal filter of X. By the above proposition, we get that (F) is an ideal of X. Clearly F is proper filter of X. Suppose 1 (F). Then 0 = 1N F which is a contradiction. Hence (F) is proper ideal of X. Let x (F). Then xN F. Suppose [ (F) {x}] X. Then 1 [ (F) {x}], which means xNNN = (xN * 1N)N (F). Hence xNNNN = F. Since x xNN xNNNN, we get x F. Since F is a maximal filter, we get áF {x}ñ = X. Hence 0 áF {x}ñ. Since X is selfdistributive, we get xN = x * 0 F which is a contradiction. Thus [ (F) {x}] = X, which concludes that (F) is a maximal ideal of X.

Definition 2.7: Let X be a BE-algebra. Then the radical of X, written as rad(X), is defined as,

where Max(X) is the family of all maximal ideals of X.

It is clear that rad(X) always exists for a BE-algebra. In the contemporary algebra, the following is a standard terminology. We say that a BE-algebra X is semi-simple if rad(X) = {0}. We first observe the non-trivial examples:

Example 2.8: Let X = {0, a, b, 1}. Define an operation * on X as follows:

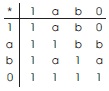
Clearly (X,*, 0, 1) is a bounded BE-algebra. It can be easily verified that the sets I₁ ={0}, I₂ = {0, a}, I₃ = {0, b} are ideals of X in which I₂ and I₃ are the only maximal ideals. Hence rad(X) = I₂ ⋂ I₃ = {0}. Therefore X is semi-simple.

Example 2.9: Let X = {0, a, b, c, d, 1}. Define an operation on X as follows:

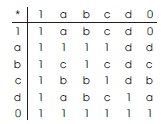
Clearly (X,*, 0, 1) is a bounded BE-algebra. It is easy to check that I₁ = {0}, I₂ = {0, a}, I₃ = [0, b}, I₄ = {0, c}, I₅ = {0, a, b} and I₆ = {0, a, c} are ideals of X in which I₅ and I₆ are only maximal ideals of X. Hence rad(X) = I₅ ⋂ I₆ = I₂ ≠ {0}. Therefore X is not a semi-simple.

Theorem 2.10: A transitive BE-algebra X is semi-simple if and only if for each 0≠ x X, there exists a proper ideal I of X such that [I {x}] = X.

Proof: Assume that X is semi-simple. Then 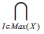I = {0}. Let 0 ≠ x  ϵ X. Then there exists a maximal ideal I of X such that x ≠I (otherwise, if every maximal ideal contains x, then 0≠xϵ  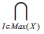= {0}). Since I is maximal, we get [I È { }] = X.

Conversely, assume the condition. Suppose I ¹ {0}. Choose 0 ¹ x Î I. By the assumed condition, there exists a proper ideal I of X such that [I È {x}] = X. Hence x Î I. Consider T= {J J is an ideal of X, x Ï J and I Í J}. Clearly I Î T and T ¹ Ø. Clearly, T is a partially ordered set, with the set inclusion, in which every chain has an upper bound. By the Zorn's lemma, T has a maximal element say I . Then x Ï I and I Í I . Suppose there exists a proper ideal M of X such that I Í IM Í X. By the maximality of M, we get x Î M. Hence X = [I È {x}] Ì [M È {x}] = M. Thus I is a maximal ideal of X and x ÏI , 0 0 which is a contradiction. Therefore I = {0}, which means that X is semi-simple.

Theorem 2.11: Let X be a self-distributive BE-algebra. Then, for every 0 ¹ x ÎX there exists a maximal ideal I of X such that x Ï I.

Proof: Let 0 ¹ x Î X. We first claim that [xN] is a proper ideal of X. Suppose 1 Î [xN]. Since X is self-distributive, we get xNNN = xNN 1N = 1. Hence x £ xNN £ xNNNN = 0. Thus x * = 0, which is a contradiction. Therefore [xN] is a proper ideal of X. Then there exists a maximal ideal I of X such that [xN] Í I. Suppose x Î I. Then (xN * 1N)N = xNNN £ xN Î [xN] Í I. Hence (xN * 1N)N Î I. Since x Î I, we get 1 Î I which is a contradiction. Therefore I is a maximal ideal of X such that x Ï I.

Corollary 2.12: Every self-distributive BE-algebra is semi-simple.

Now we introduce the notion of radicals of ideals in BE-algebras.

Definition 2.13: Let I be a proper ideal of a BE-algebra X. The intersection of all maximal ideals of X that contain the ideal I is called the radical of I and is denoted by rad(I).

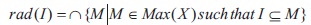
Proposition 2.14: Let M be a maximal ideal of a BE-algebra X. Then rad(M) = M.

Proof: Obviously, by Definition 2.13, rad(I) is an ideal of a BE-algebra and I Í rad(I). Further, if M is a maximal ideal of X then rad(M) = M.

Example 2.15: Let X = {1, a, b, c, d, e, f, 0}. Define an operation * on X as follows:

Clearly (X, *, 0, 1) is a bounded BE-algebra. It can be easily verified that the set I = {0, d}, J = {0, c} and K = {0, a, b, c} are proper ideals of X. It is easy to verify that rad(I) = I, rad(J) = {0, a, b, c} and rad(K) = K.

Theorem 2.16: Let I be a proper ideal of a self-distributive BE-algebra. Then,

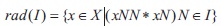
Proof: Put K = {x Î X (xNN * xN)N Î I}. Let x Î K. Suppose x Ï rad(I). Then there exists a maximal ideal M of X such that I Í M and x Ï M. Since M is maximal and by Proposition 2.3, we get xN Î M. Since x Î K, we get (xNN * xN)N Î I Í M. Since xN Î M and M is an ideal, we get x Î M which is a contradiction. Hence x Î rad(I). Therefore K Í rad(I).

Conversely, let x Î rad(I). By the definition of rad(I), we get x Î M for each maximal ideal M of X with I Í M. Suppose (xNN xN)N Ï I. Then there exists a maximal ideal M¢ of X such that I Í M¢ and (xNN xN)N Ï M¢. * Since I Í M¢, we get x Î M¢. Since x Î M¢, then by the property of ideals (xNN * xN)N Î M¢ which is a contradiction. Hence (xNN * xN)N Î I, which means x Î K. Therefore rad(I) Í K and hence rad(I) = K = {x Î X (xNN xN)N Î I}.

Proposition 2.17: Let I be an ideal of a self-distributive BE-algebra X. Then I is a proper ideal of X if and only if rad(I) is a proper ideal of X.

Proof: It follows Definition 2.13 and Theorem 2.16.

Lemma 2.18: Let I, J be proper ideals of a self-distributive BE-algebra X. Then

Proof: (1) and (2) are immediate consequences from the Theorem 2.16. (3) It follows from Proposition 2.17. Proposition 2.19: Let {I } be a family of ideals of a BE-algebra X. Then,

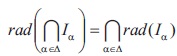
Proof: It can be routinely verified by using the Theorem 2.16.

Let I = {1, 2,..., n} and {X = (X , , 0, 1) i Î I be a finite family of bounded BE-algebras. Define the direct product of n i i * n bounded BE-algebras X ,X ,..., X as an algebraic structure.

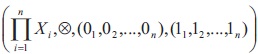
where 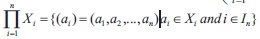and whose operations are defined as,

for any 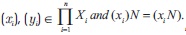Then clearly the direct product is a bounded BE-algebra with largest element (1 ) and i i i the smallest element (0 ). Note that 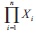is self-distributive whenever each X is self-distributive.

Proposition 2.20: Let {J ) , where I = {1, 2,..., n}, be a finite family of ideals of a BE-algebra X. Then,

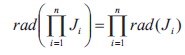
Proof: It can be routinely verified by using the Theorem 2.16. Lemma 2.21 Borzooei et al. (2014): Let X and Y be two BE-algebras. For any BE-homomorphism f : X ® Y , the dual kernel is an ideal of X. Proposition 2.22: Let X and Y be two BE-algebras and f : X ® Y be a BE-homomorphism. Then; 

(1) f^-1 (I) is an ideal of X for any ideal I of Y .

(2) If f is BE-isomorphism then f (I) is an ideal of Y for any ideal I of X.

Proof: Let f : X ® Y be a BE- homomorphism. 

(1). Suppose I is an ideal of Y. Let x, y ϵ X be such that x Î f (I) and (xN * yN)N Î f (I). Then f^-1 (x) Î I and (f (x)N * f ^-1(y)N)N = f ^-1((xN yN)N) Î I. Since f v(x) Î I and I is an ideal, we get f (y) Î I. Hence y * Î f (I). Thus f (I) is an ideal of X. 

(2). Suppose I is an ideal of X. Let x, y Î Y be such that x Î f (I) and (xN * yN)N Î f (I). Then f^-1 (x) Î I and f^-1 ((xN*yN)N) Î I.  Now (f (x)N * f (y)N)N = (f (xN) * f (yN))N = (f (xN * yN))N = f ((xN * yN)N) Î I. Since f (x) Î I and I is an ideal, we get f (y) Î I. Which implies, y Î f (I). Hence f (I) is an ideal of Y.

Proposition 2.23: Let X and Y be two BE-algebras and f : X ® Y be a BE-homomorphism. Then Dker(f ) = d(ker(f )).

Proof. Clearly Dker(f ) is an ideal of X. Let x Î Dker(f ). Then f (x) = 0. Thus f (xN) = (f (x))N = 0N = 1. So, xN Î ker(f ). Hence x Î d (ker(f )). Conversely, Let x Î d(ker(f )). Then xN Î ker(f ). Thus f (xN) = 1. Now, f (xNN) = (f (xN))N = 1N = 0. Since x £ xNN, we get f (x) £ f (xNN). So f (x) = 0. Hence x Î Dker(f ). Therefore Dker(f ) = d(ker(f )).

Proposition 2.24: Let X and Y are two BE-algebras where X is self-distributive. Suppose y : X ® Y is a BE-homomorphism. Then

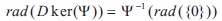
Proof: By Theorem 2.16, for x Î rad(Dker(y))

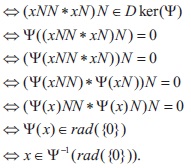
Proposition 2.25: Let X and Y be two BE-algebras, where X is self-distributive. Suppose that y : X ® Y is a BE-homomorphism. If I is an ideal of X and I is an ideal of Y. Then we have,

Proof: (1). Since I is an ideal of Y, it is easy to check that y (I ) is an ideal of X. Let x Î X. Then by Theorem 2.16, we get

Hence rad(y (I )) =y(rad(I)).

(2). Let I be an ideal of X and y be a BE-isomorphism. Then y(I ) is an ideal of Y.

Now, let y Î (rad(I)). Then there exists x Î rad(I ), such that y = y (x). Now

which means y = Y(x) Î rad(Y(I )). Therefore Y (rad(I )) Í rad( (I )).

Conversely, let y Î rad(Y (I )). Then by Theorem 2.16, we get (yNN * yN)N Î Y (I ).

Since y is a BE-isomorphism, there exists x Î I such that y(x) = (yNN * yN)N. Thus

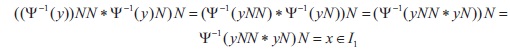
Thus, by Theorem 2.16, we get y (y)Î rad(I ). Hence y Î y (rad(I )). Therefore, rad(y(I )) Í y(rad(I )) and hence rad(y(I )) = y 1 1 1 1 1 (rad(I )). 1

Theorem 2.26 Borzooei et al. (2014): Let I be an ideal of a self-distributive BE-algebra X. For any x, y Î X, define a relation q I on X as follows:

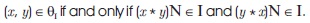
Then q is a congruence on X. I

From the above result, it is easy to see that the quotient algebra X / I = {I x Î X} (where I is the congruence class of x x x modulo q) is a bounded BE-algebra in which the binary operation * is defined as I I = I I x * y x*y for x, y Î X and the unary operation N is defined as (I )N = I for all x Î X. Moreover, the quotient algebra X/I contains the smallest element I . x xN 0

Corollary 2.27: Let I be an ideal of a self-distributive BE-algebra X and I is a congruence on X. Then I = I.

Proof: Suppose I is an ideal of a self-distributive BE-algebra X and q is a congruence on X. Now, let x Î I . Then xNN = (x 0) I 0 * N Î I. Since x £ xNN, we get x Î I. Therefore I Í I. Again, let x Î I. Then (x 0)N = xNN Î I. Clearly (0 x)N = 1N = 0 Î I. 0 * * Hence (x, 0) Î I , which implies x Î I . Thus I Í I . Therefore I₀ = I. 

Proposition 2.28: Let I be a proper ideal of a self-distributive BE-algebra X. Then rad({0}/I) = rad(I)/I.

Proof: Let I be a proper ideal of X. By Theorem 2.16, we get;

In this section, the notion of semi-maximal ideals is introduced in BE-algebras through the radical of ideals. Some equivalent conditions are derived for every semi-maximal ideal of a BE-algebra to become a maximal ideal. Properties of semimaximal ideals are derived with respect to homomorphisms, cartesian products and congruences.

Definition 3.1: A proper ideal I of a BE-algebra X is said to be semi-maximal if rad(I) =I.

Example 3.2: Let X = {1, a, b, c, d, 0}. Define an operation * on X as follows:

Clearly (X, *, 0, 1) is a bounded BE-algebra. Let I = {0} and J = {0, d} are a proper ideals of X. Note that rad(I) = {0, d} and rad(J) = {0, d} = J. Here we observed that J is a semi-maximal ideal but I is not a semi-maximal ideal.

Proposition 3.3: Let I be a proper ideal of a self-distributive BE-algebra X. Then rad(I) is the smallest semi-maximal ideal of X such that I Í rad(I).

Proof: By Lemma 2.18 (2), rad(I) is a semi-maximal ideal of X. Let J be a semi-maximal ideal of X such that I Í J. By Lemma 2.18(1), rad(I) Í rad(J) = J. Hence rad(I) is the smallest semi-maximal ideal of X such that I Í rad(I).

Proposition 3.4: Every maximal ideal of a self-distributive BE-algebra is semi-maximal.

Proof: Let M be a maximal ideal of a BE-algebra X. Clearly M Í rad(M). Let x Î rad(M). Then, we get (xNN*xN)N Î M. Suppose x Ï M. Then by Proposition 2.3, we get xN Î M. Since (xNN*xN)N Î M, then we get x Î M, which is a contradiction. Hence x Î M. Therefore rad(M) = M, which means M is semi-maximal.

The converse of the above proposition is not true. For, consider the following:

Example 3.5: Let X = {1, a, b, c, 0}. Define an operation * on X as follows:

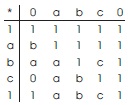
Clearly (X, *, 0, 1) is a bounded BE-algebra. It can be easily verified that the set I = {0, a}, I = {0, a, b} and I = {0, a, c} are 1 2 3 proper ideals of X. Also I , I are maximal ideals of X that contain I . Now

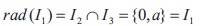
Hence I is a semi-maximal ideal of X but not maximal because of I₁ ⊂ I₂, I₃.

In the following theorem, we derive a set of equivalent assertions for a semi-maximal ideal of a BE-algebra to become a maximal ideal.

Theorem 3.6: Let I be a semi-maximal ideal of a self-distributive BE-algebra X. Then the following assertions are equivalent:

(1) I is a maximal ideal;

(2) rad(I) is a maximal ideal;

(3) for any x Î X, x Ï rad(I) implies xN Î I.

Proof: (1) ⇒ (2): Assume that I is a maximal ideal of X. Since I semi-maximal, we get rad(I) = I. Since I is maximal, it yields that rad(I) is a maximal ideal of X.

(2) ⇒ (3): Let x Î X. Suppose x Ï rad(I). Since rad(I) is maximal, then by Theorem 2.3, we get xN Î rad(I). Since I is semimaximal, we get xN Î rad(I) = I.

(3) ⇒ (1): Let x Ï I. Since I is semi-maximal, we get rad(I) = I. Hence x Ï rad(I). By (3), we get xN Î I. Then by Theorem 2.3, we get I is a maximal ideal.

Proposition 3.7: Let X be a self-distributive BE-algebra, if X is dense, then every ideal is a semi-maximal ideal.

Proof: Assume that X is a dense BE-algebra. Let 0 ¹ x Î X then xN = 0. Let I be an ideal of X. Suppose x Ï I. Since xN = 0 Î I. Then by Proposition 2.3, we get I is a maximal ideal. Then by Proposition 3.4, I is a semi-maximal ideal.

Proposition 3.8: Let F be a proper filter of a self-distributive BE-algebra X. If F is maximal, then d(F) is a semi-maximal ideal of X where d(F) = {x Î X xN Î F}.

Proof: By Proposition 2.6, we get d(F) is a maximal ideal of X. Hence by Proposition 3.4, d(F) is a semi-maximal ideal of X. Proposition 3.9: Let {I } be a family of semi-maximal ideals of a self-distributive BE-algebra X.

Then, is a semi-maximal aaÎD ideal of X. Proof: Since each I is a semi-maximal ideal of X, we get rad(I ) = I for each a Î D. Then by Proposition 2.19, we get

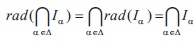
and therefore is a semi-maximal ideal of X.

Proposition 3.10: Let {J } , where I = {1, 2,...,n}, be a finite family of semi-maximal ideals of a self-distributive BE-algebra X. i iÎIn n Then J is a semi-maximal ideal of the product algebra Xn.

Proof: Since each J is a semi-maximal ideal of X, we get rad(J ) = J for each i Î I . Then by Proposition 2.20, we get

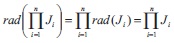
and therefore J is a semi-maximal ideal of Xn.

Proposition 3.11: Let X and Y be two self-distributive BE-algebras, and f : X ® Y be a BE- homomorphism. Then

(1) If I is a semi-maximal ideal of Y, then f (I) is semi-maximal in X.

(2) If {0} is semi-maximal in X, then Dker(F) is semi-maximal in X.

(3) If f is BE-isomorphism and I is a semi-maximal ideal of X, then f (I) is a semi-maximal ideal of Y.

Proof: (1). Let I be a proper ideal of Y. Suppose I is semi-maximal. Then rad(I) = I. Let X Î X be such that x Î rad(f (I)). Then -1 -1 (xNN * xN)N Î f (I). Then (f (x)NN * f (x)N)N = f ((xNN * xN)N) Î I. Hence f (x) Î rad(I) = I, which means x Î f (I). Thus rad(f -1 -1 -1 (I)) Í f (I). Therefore f (I) is a semi-maximal ideal of X.

(2). Assume that {0} is a semi-maximal ideal of X. Then rad({0}) = {0}. Clearly Dker(f ) is an ideal of X and Dker(f ) Í rad(Dker(f )). Let x Î X be such that x Î rad(Dker(f )). Then (xNN * xN)N Î Dker(f ). Hence (f (x)NN *f (x)N)N =(f (xNN) * f (xN))N = f (xNN * xN)N = f ((xNN * xN)N) = 0 Î {0}, which gives f (x) Î rad({0}) = {0}. Thus x Î Dker(f ), which concludes that rad(Dker(f )) Í Dker(f ). Hence rad(Dker(f )) = Dker(f ). Therefore rad(Dker(f )) is semi-maximal in X.

(3). Let I be a semi-maximal ideal of X. Since f is BE-isomorphism, we get f (I) is an ideal of Y. Since I is a semi-maximal, we get rad(I) = I. By Proposition 2.25(2), we get rad(f (I)) = f (rad(I)) = f (I). Hence f (I) is a semi-maximal ideal of Y.

Lemma 3.12: Let I be a proper ideal of a self-distributive BE-algebra X and I be the congruence on X given by (x, y) Î q if I and only if (x * y)N Î I and (y * x)N Î I. Then,

(1) {0}/I is an ideal of X=I where {0}/I = {I (x, 0) Î q}. x I

(2) I Î rad(I) / I implies x Î rad(I). x

(3) rad(I) / I is a semi-maximal ideal of X / I.

Proof: (1). Clearly I0 Î {0}/I. Let Ix, (IxN * IyN)N Î {0}=I. Then I(xN*yN)N Î {0}/I. Hence (x, 0) Î qI and ((xN * yN)N, 0) Î qI. Thus xNN = (x * 0)N Î I and (xN * yN)NNN = ((xN * yN)N * 0)N Î I. Since x £ xNN and (xN * yN)N £ (xN * yN)NNN, we get x Î I and (xN * yN)N Î I. Since I is an ideal of X, we get y Î I. Thus (y * 0)N = yNN Î I and (0 * y)N = 0 Î I. Hence (y, 0) Î qI , which gives I Î {0}/I. Therefore {0}/I is an ideal of X/I. y

(2). Let x Î X and I Î rad(I)/I. Then I = I for some a Î rad(I). Hence (x, a) Î I , which provides (x a)N Î I. Since (aN xN)N £ x x a * * (x * a)N, we get (aN * xN)N Î I Í rad(I). Since a Î rad(I), we get x Î rad(I).

(3). Since 0 Î I Í rad(I), we get I Î rad(I)/I. Let I , (I N * I N)N Î rad(I)/I. Then I Î rad(I)/I. By (2), we get x Î rad(I) and 0 x x y (xN*yN)N (xN * yN)N Î rad(I). Since rad(I) is an ideal of X, we get y Î rad(I). Hence Iy Î rad(I)/I. Therefore rad(I)/I is an ideal of X/I. We now show that rad(I)/I is semi-maximal in X/I. Clearly rad(I)/I Í rad(rad(I)/I). Conversely, let I Î rad(rad(I)/I). Then by Theorem x 2.16, we get I = ((I )NN (I )N)N Î rad(I)/I. Then by (2), we get (xNN xN)N Î (xNN*xN)N x * x * rad(I). So by Theorem 2.16 and Lemma 2.18 (2), we get x Î rad(rad(I)) = rad(I). Hence I Î rad(I)/I. Therefore rad(rad(I)/I) Í rad(I)/I, which gives rad(I)/I is x semi-maximal in X/I.

Theorem 3.13: Let X be a self-distributive BE-algebra and I be a proper ideal of X. Then I is a semi-maximal ideal of X if and only if {0}/I is a semi-maximal ideal of the quotient algebra X/I.

Proof: Assume that I is a semi-maximal ideal of X. Then rad(I) = I. By Lemma 3.12(1), we have {0}/I is an ideal of X/I. Clearly {0}/I Í rad({0}/I). Let I Î rad({0}/I). x Then I = ((I )NN * (I )N)N Î {0}/I. Now

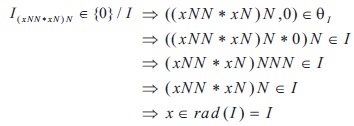
Since I is an ideal, we get (x 0)N = xNN Î I. Also (0 x)N = 0 Î I. Hence (x, 0) Î q , which means I Î {0}/I. Therefore * * I x rad({0}/I) = {0}/I.

Conversely, assume that {0}/I is a semi-maximal ideal of X/I. Then rad({0}/I) ={0}/I. Clearly I Í rad(I). Let x Î rad(I). Then (xNN * xN)N Î I. Since I is an ideal, we get ((xNN * xN)N * 0)N = (xNN * xN)NNN Î I. Also (0*(xNN * xN)N)N = 0 Î I. Thus ((xNN xN)N, 0) Î q. Hence,

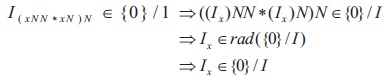
which gives (x, 0) Î q . Hence xNN = (x 0)N Î I. Since I is an ideal, we get x Î I. Thus rad(I) Í I. Hence rad(I) = I. Therefore I I * is a semi-maximal ideal of X.

Theorem 3.14: Let X be a self-distributive BE-algebra and I is a proper ideal of X. If X/I is dense, then I is a semi-maximal ideal of X.

Proof: Let X be a proper ideal of X. Assume that X/I is dense. Suppose x Ï I. Then I Ï {0}/I (Otherwise, if I Î {0}/I, then (x, 0) x x Î q. Hence x £ xNN = (x 0)N Î I, which is a contradiction). Since X/I is dense, we get (I )N = I Î {0}/I. Thus (xN, 0) Î q. I * x 0 I Since xN £ xNNN = (xN * 0)N Î I. By Proposition 1.9(1), we get xN Î I. Hence by Proposition 2.3, we get I is maximal and therefore by Proposition 3.4, we get I is a semi-maximal ideal.

In this paper, we introduced the notion of radicals of ideals in BE-algebras and derived some significant properties of these radicals in terms of direct products and homomorphisms. The notion of semi-maximal ideals is introduced in BE-algebras and some properties of the semi-maximal ideals are investigated. A set of equivalent conditions is given for every semi-maximal ideal of a self-distributive BE-algebra to become a maximal ideal. Some properties of semi-maximal ideals are investigated in terms of homomorphisms, cartesian products and congruences. For the future research, we investigate some topological properties of semi-maximal ideals with the help of minimal prime ideals and maximal ideals of BE-algebras.