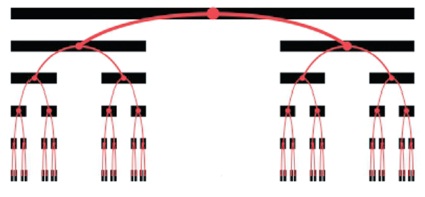
Figure 1. Cantor Set
In everyday life, we rarely hear the mysterious word “fractal”, but we encounter them on a daily basis. Nature exhibits fractals in Trees, mountains, snow, plants, and even the circulatory system have fractal structures. Fractals can be applied in various areas from image compression algorithms to the study of blood vessels of living organisms. A fractal is a never-ending pattern. Fractals are infinitely complex patterns that are self-similar across different scales. They are created by repeating a simple process over and over in an ongoing feedback loop. Driven by recursion, fractals are images of dynamic systems – the pictures of Chaos. Geometrically, they exist in between our familiar dimensions. Fractal patterns are extremely familiar, since nature is full of fractals.
In Mathematics, a fractal is a self-similar subset of Euclidean space whose fractal dimension strictly exceeds its topological dimension. Fractals appear the same at different levels, as illustrated in successive magnifications of the Mandelbrot set. Fractals exhibit similar patterns at increasingly small scales called self-similarity, also known as expanding symmetry or unfolding symmetry; if this replication is exactly the same at every scale, as in the Menger sponge, it is called affine selfsimilar. Fractal geometry lies within the mathematical branch of measure theory (Fractals, 2020).
In the language of Mathematics, a fractal is a set with the property of self-similarity. In other words, each member of the set is an exact or approximate copy of a part of itself. One of the simplest examples to help us understand fractals is a Koch snowflake.
The Koch snowflake occupies a limited area, for example, it can be limited to a circle of a certain length. But meanwhile, the snowflake has an infinite perimeter (!). Say that the triangle's side is one whole. Then, with each step, its length increases 4/3 times. It is easy to derive the ratio of the length of the side
at n step In = (4/3)n-1
As n approaches infinity, the side length will also approach infinity.
The Koch snowflake is a geometric fractal. As are the Cantor set (Figure 1), the Sierpinski triangle, the Peano curve (Spaceth filling curve) (Figure 2), and many others. It was with these models that the theory of fractals began in the 19th century, due to the fact that the properties of self-similarity are most apparent in geometric fractals.

Figure 1. Cantor Set
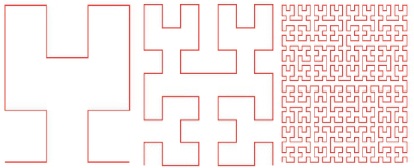
Figure 2. Peano Curve
Fractals are described by simple rules, which must be performed repeatedly. The advent of the computer caused a second wind in the study of fractals, as they were perfectly suited to perform these operations.
Fractals are a highly abstract Mathematical concept, but, surprisingly, we frequently encounter objects in nature which possess their main property — self-similarity. This is linked to two main trends in the practical application of fractal theory. Firstly, there are attempts to copy a natural fractal object using a simplified mathematical model. Computer animation achieved great results in this trend. Secondly, there are efforts to analyze a natural object and reveal the fractal structures within it.
Corals, sea stars, hedgehogs, broccoli, coastlines, mountain ranges, and snowflakes all possess fractal properties. One of the clearest examples of this structure is a tree. Many branches extend from the trunk of the tree, and from those, smaller branches, and so on. The tree possesses the main property of fractals — self-similarity: each branch is similar to the whole tree.
In the 14th century, Leonardo da Vinci developed a rule about the thickness of tree branches: “all the branches of a tree at every stage of its height when put together are equal in thickness to the trunk.” Scientists have not found an exact explanation for this phenomenon: some associate it with the transportation of water in the bark of the tree; while others believe it is due to the tree's resistance to external mechanical influences.
The human circulatory system is also arranged in a similar way: from the arteries extend thinner vessels — arterioles, and from the arterioles — capillaries, the smallest vessels. Due to these properties of blood vessels, scientists have been able to study and explain various anomalies in the human body.
Coastlines are the most unusual example of fractals. If in the rest of these examples, a person could visualize the object in entirety, coastlines are the more complicated: standing on the ground, you can only observe a small portion of the shore.
Measuring the length of a shoreline is an extremely difficult task. Coastal bends have different lengths, from a few meters to thousands of kilometers, which make it challenging to find and measure the smallest segments of the coast. So, if you divide the coast into segments of 50 kilometers and count the total length of the segments, the result will be radically different from what you get if you divide the coastline into 100-km segments and sum those. English Mathematician Lewis Fry Richardson encountered this paradox in 1951 when he noticed that Portugal calculated the length of their land border with Spain to be 987 kilometers, while Spain thought it was 1214 km. They solved this problem by adopting the smallest fragment as the unit of measurement. For example, if the length of a coastline is measured in kilometers, then small bends which are much less than one kilometer long, are not taken into account (Figure 3).
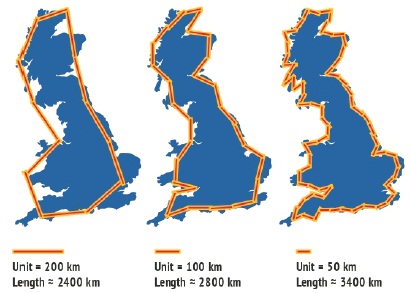
Figure 3. The Coastline Paradox
Fractals are applied in various fields such as Computer imaging, Art, Medicine and construction.
A fractal algorithm for image compression has a high compression ratio: the image becomes much smaller in size, which saves memory on the computer. The compression ratio when using a fractal algorithm is roughly comparable to the most popular method of compression — JPEG. The essence of the method is the detection of self-similar portions of the image, which allows for the subsequent increase in the size of the compressed image while preserving its quality (Figure 4).

Figure 4. Image Compression
Clouds, trees, flowers, mountains, the sea, and many other natural objects which can be seen in computer games and cartoons are generated with the help of fractal algorithms. When using the fractal method, you do not need to draw each detail of a graphic object separately (a tree branch, mountaintop, or flower petal); it suffices to simply set the initial parameters of the algorithm and the rest of the work will be done by the computer. Because of this, it is also possible to change the object quite quickly just by changing the initial parameters of the algorithm.
Modern medical equipment (MRI and tomography) allow you to obtain a huge amount of digital data about the internal organs of a patient. The computer performs a Mathematical analysis of this data and identifies fractal structures. Cancerous tumours and emphysema have a more complex structure, while healthy areas are simpler. The principle of self-similarity in a fractal allows us to reveal deviations in the very earliest stages and do so automatically, without the participation of a doctor.
Cancerous tumours are made through the anomalous, rapid growth of cells, which are accompanied by the formation of new and disordered blood vessels. Healthy blood vessels have an ordered fractal structure (Figure 5).
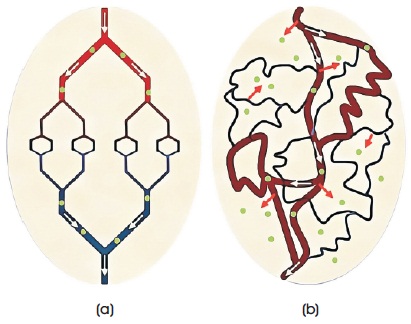
Figure 5. a) Normal Vasculature b) Tumor Vasculature
Modern engineers use high-tech cables which are woven according to the fractal principle (the cable is formed from a bundle of cables, which are, in turn, formed from smaller wires, and so on). The Golden Gate Bridge (San Francisco, USA) is one example in which such technology was used (Figure 6).
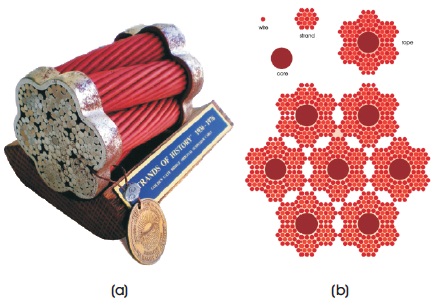
Figure 6 (a,b) Cross Section of the Golden Gate Bridge’s Cable
The consensus is that theoretical fractals are infinitely self-similar, iterated, and detailed Mathematical constructs having fractal dimensions, of which many examples have been formulated and studied in great depth. Fractals are not limited to geometric patterns, but can also describe processes in time. Fractal patterns with various degrees of self-similarity have been rendered or studied in images, structures and sounds and found in nature, technology, art, architecture and law. Fractals are of particular relevance in the field of chaos theory, since the graphs of most chaotic processes are fractals. Many real and model networks have been found to have fractal features such as self similarity (Fractal, n.d.).