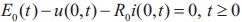
The main purpose of the present paper is to analyse the processes in a lossy transmission line terminated by in-series connected nonlinear RCL-loads. The distortionless propagation of the TEM-waves along the line under the Heaviside's condition has been investigated in a previous paper. Here we assume that the Heaviside condition is not satisfied. This leads to difficulties which can be overcome by a different type operator presentation of the mixed problem for the lossy transmission line. First, we formulate boundary conditions using the Kirchhoff's law, then transform the system in an operator form, and apply the fixed point method to obtain an existence-uniqueness theorem for a generalized solution. The uniqueness of solution is lost along the whole length of the line. Finally, we demonstrate the conditions of the main theorem on a typical example.
The lossy transmission lines terminated by various circuits have many applications to radio engineering devices, in particular to antenna feeder devices, various type waveguides and so on. Many cases are considered in (De Broglie, 1941; Holt, 1963; Jordan & Balmain, 1968; Ramo, Whinnery, & Van Duzer, 1994; Chua, Desoer, & Kuh, 1987; Chua & Lin, 1980; Rosenstark, 1994; Maas, 2003; Misra, 2004; Miamo & Maffucci, 2001; Martin, 2015; Singh, 2013; Makwana & Bhalja, 2016; Ruikar, 2016; Kalaga & Yenumula, 2016; Patil & Behere, 2019; Kapoor, 2019; Dinakaran, 2015; Gaurav & Chauhan, 2016; Raghuwanshi, Kumar, & Pandey, 2011; Sharma, Sandhu, & Sharma, 2018). Many circuits in radio engineering contain as a component the basic loads connected in series. In (Angelov & Hristov, 2011), they have investigated a lossy transmission line terminated by in series connected RLC- elements. We have applied the method from (Angelov, 2013) for solving the mixed problem for hyperbolic transmission line system. Conditions are obtained guaranteeing distortionless propagation of TEM waves. The essential role plays the Heaviside's condition h=(R/L)-(G/C)=0, where R, L, C, G are the specific parameters of the lossy transmission line. It is known, however, that over time, the values of these parameters change and the Heaviside's condition is violated. That is why, the main purpose of the present paper is to investigate the same problem from (Angelov & Hristov, 2011), but without the Heaviside's condition. This does not allow the approach developed in (Angelov, 2013) to be applied. We extend the A. D. Myshkis method, cf. (Angelov, 2015; 2016) to reduce the mixed problem for hyperbolic transmission line system to an operator form and then apply the fixed point technique. We show explicitly that we have to short the line length to obtain a unique solution. On the rest part of the line, the uniqueness of the solution vanishes.
The paper consists of five sections. In Section 1, the boundary conditions are derived using the Kirchhoff's law and formulate the mixed problem for transmission line equations. In Section 2, the hyperbolic system is reduced to a diagonal form. In Section 3, the nonlinearities of the loads are analyzed and an operator formulation of the mixed problem is given. In Section 4, an existence-uniqueness theorem is proved, but not on the whole line. The authors have used the fixed point method. In Section 5, the authors demonstrate conditions of the existence-uniqueness theorem using specific numerical data. And finally, the conclusion is given at the end.
In accordance with the Kirchhoff's law (cf. Figure 1) for the left end of the line we have,
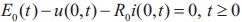
For the voltage at the right end uright end we obtain:
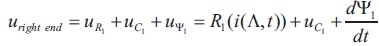
We use usually accepted denotations R1(i), C1(i), L1(i), for the characteristics of the nonlinear loads.
To calculate the voltage of the condenser C1, we proceed from the relation (assuming uC1(0)=0):

In order to calculate the voltage of the inductor L1, we use the relation:

For the right end, that is x = ⋀, we obtain
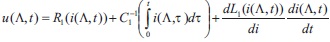
We proceed from the lossy transmission line system (or generalized telegrapher equations) of equations

where the unknown functions are voltage u(x, t) and current i(x, t) along the line, L is per unit-length inductance, C - per unitlength capacitance, R - per unit-length resistance, G - per unit-length conductance, ⋀ - the length of the transmission line, and ν=1/√LC - the speed of propagation of the TEM-waves. This system is of hyperbolic type and we can formulate a mixed problem: to find a solution (u(x, t), i(x, t)) for (x, t) ϵ π = {(x, t) ϵ R2 : 0 ≤ x ≤ ⋀, t ≥ 0}, satisfying the initial conditions u(x, 0)= u0(x), i(x, 0) = i0(x) for x ϵ [0, L], where u0(x), i0(x) are prescribed functions. The boundary conditions were derived on the basis of the Kirchhoff's laws in Figure 1.
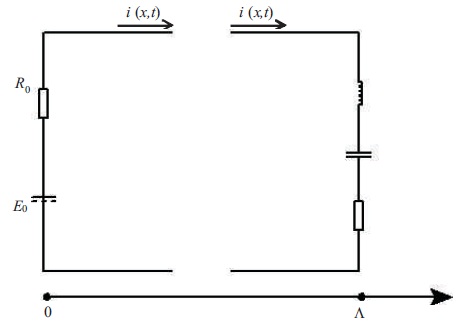
Figure 1. Lossy Transmission Line Terminated by in Series Connected RLC-Elements
The boundary condition for x=0 is

and for x=⋀
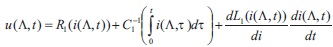
To reduce the mixed problem to an initial value problem on the boundary we follow (Angelov, 2015). Rewrite equation (1) in a matrix form:
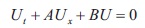
where
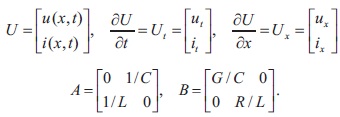
To transform the matrix 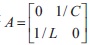 in a diagonal form we form, the matrix H by eigenvectors,
in a diagonal form we form, the matrix H by eigenvectors, 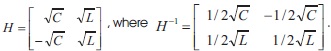 , where
, where  .It is known that
.It is known that 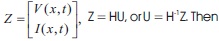 .
.
Then we introduce new variables Then
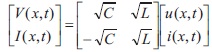
and
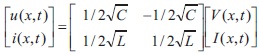
Substituting U = H-1Z in (2) we obtain,

or
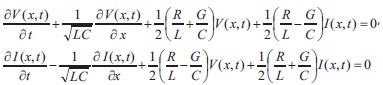
Here we emphasize that the Heaviside condition is not fulfilled, that is,  Introducing denotation
Introducing denotation 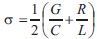 we make one more substitution
we make one more substitution 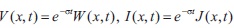 and then equation (6) becomes
and then equation (6) becomes
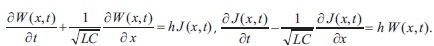
Since  we can't apply the method from (Angelov, 2015). By using the transformation formula,
we can't apply the method from (Angelov, 2015). By using the transformation formula,
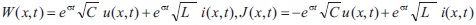
and their inverse ones

we obtain the initial conditions and respect to the new variables W(x, t) and J(x, t):
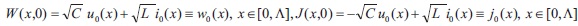
Assumptions (L): We assume that the I-L characteristic of the inductive element satisfies conditions:
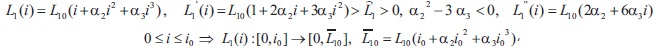
We need the estimate 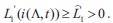
Assumptions ( C): The capacitive element has a characteristic  , where are prescribed positive constants.
, where are prescribed positive constants.
In view of the obvious singularity of the function C1(u) we consider C1(u) for 
Since 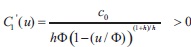 and
and 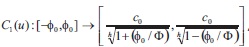 the inverse function of C1(u) does exist and
the inverse function of C1(u) does exist and  Besides since
Besides since  , the C1(u) is min
, the C1(u) is min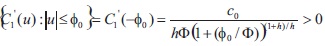 We have also
We have also 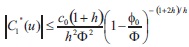 and
and 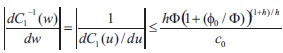
Assumptions (R): 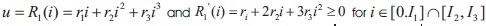 and
and 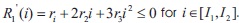 . We assume that
. We assume that 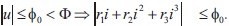
With respect to the new variable (in view of 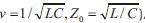 we have to solve the following mixed problem (MP): to find a solution
we have to solve the following mixed problem (MP): to find a solution 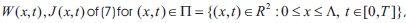 with boundary conditions
with boundary conditions
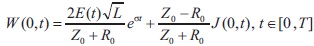
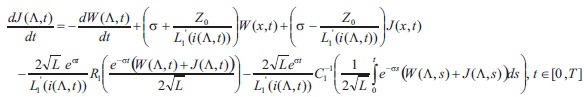
where
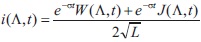
Following (Angelov, 2016; Angelov & Hristov, 2016) we consider the Cauchy problem for the characteristics:
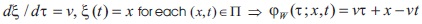
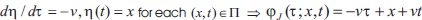
Functions λw(x,t)= ν>0 and λJ(x,t)= -ν<0are continuous ones and imply a uniqueness to the left from t of the solution 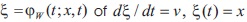 of and respectively of
of and respectively of 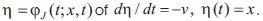
Denote by Xw(x, t), the smallest value of τ such that the solution 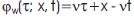 of equation (8) still belongs to P and by c(x,t) - the respective value of t for the solution ( ; x, t)=- -vτx - vt of equation (9). If (x, t)>0 then φJ(XJ(x, t); x,t)=0 or φJ(XJ(x, t); x,t)= , and respectively if (x, t)>0 then φJ(XJ(x, t); x,t)=0 or φJ(XJ(x, t); x,t)= ⋀. In our case
of equation (8) still belongs to P and by c(x,t) - the respective value of t for the solution ( ; x, t)=- -vτx - vt of equation (9). If (x, t)>0 then φJ(XJ(x, t); x,t)=0 or φJ(XJ(x, t); x,t)= , and respectively if (x, t)>0 then φJ(XJ(x, t); x,t)=0 or φJ(XJ(x, t); x,t)= ⋀. In our case
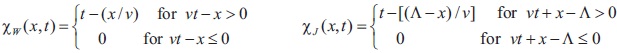
Remark 1: We notice that 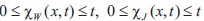
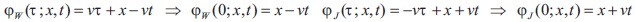
Introduce the sets
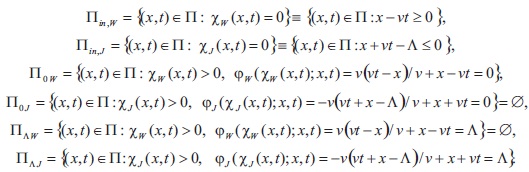
Prior to present the mixed problem in operator form we introduce
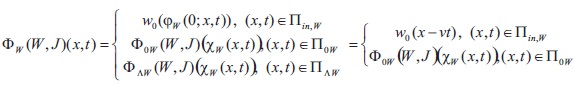
and
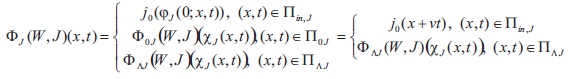
where φ0w and φ⋀J respectively are defined by the right-hand sides of corresponding boundary conditions. So we assign to the above mixed problem the following system of operator equations
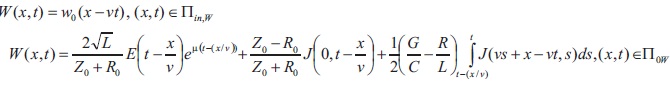

Introduce the function sets:
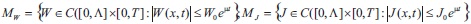
where Wo, Jo and μ>σ are positive constants. It is easy to verify that the set Mw x MJ turns out into a complete metric space with respect to the metric:
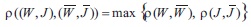
where
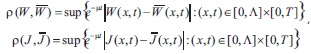
Now we define an operator by the formulas 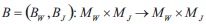

The fixed point (W, J) of the operator B:Bw (W,J);J=BJ(W,J) we call a generalized solution of the mixed problem (MP). In this manner we avoid the conformity condition (Angelov, 2015).
Lemma 1: The following estimates are valid:

Theorem 1: Let the following conditions be fulfilled:
1) E0 is continuous on 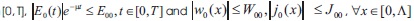 with W00, J00 and E00 sufficiently small.
with W00, J00 and E00 sufficiently small.
For sufficiently large μ> σ > 0 and some ε ϵ(0,⋀), the following inequalities are fulfilled:

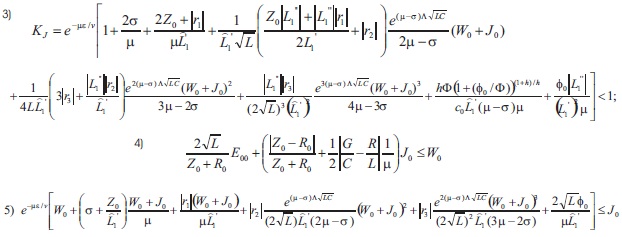
Then there exists a unique generalized solution of equation (3) for 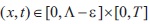
Remark 1: It is easy to see that 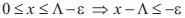
Proof: We have to show that the operator B is a contractive one. Indeed, since

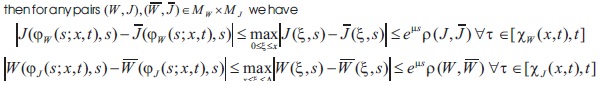
and we obtain
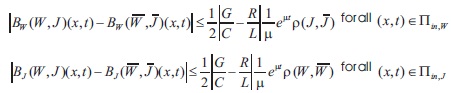
Moreover, if (x,t)ϵπow, then
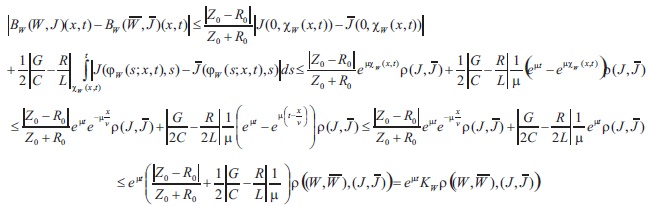
where , which implies
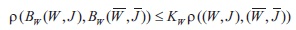
It is easy to see that Kw< 1.
Further on we take into account that for sufficiently large 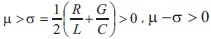 is sufficiently large too. Then for (x,t) ϵ πin,J
is sufficiently large too. Then for (x,t) ϵ πin,J
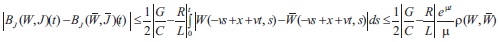
which implies 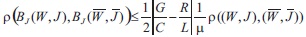
For (x,t) ϵ π⋀J we estimate the difference below for maximal value of 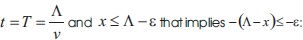

We show that B maps Mw x MJ into itself. Indeed, with the corresponding conformity conditions, all operator functions are continuous ones and: if (x,t) ϵ πow, then

Therefore, the operator B has a unique fixed point which is a generalized solution of (MP);
Theorem 1 is thus proved.
Here we collect all inequalities guaranteeing the existence-uniqueness result,
Let the transmission line be such that L=2.10-8 H/m ; C=8.10-12 F/m; R=0,4W/m; G=8 S/m;


We take the I-L characteristic of the inductive element to be:
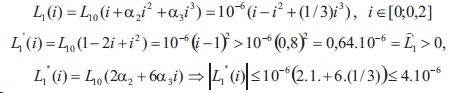
Let us choose i0 = J0.Then
Assumptions (R): 
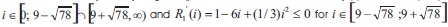 We assume that
We assume that
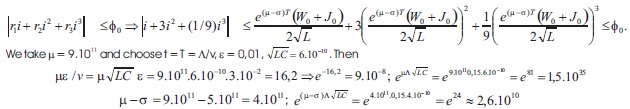
Further on we assume W0=J0=E00 and the inequalities from Theorem 1 become:

for sufficiently small W0 and W00.
It is easy to see that Theorem 1 guarantees an existence of a generalized solution of the mixed problem. For the whole interval [0, L] the solution can be extended as in (Angelov, 2016).
The systems of differential equations arising in electrical engineering are most often solved by numerical methods, the most common of which is Finite Difference Time Domain method (Chan, 2006). Here the author proposes a sequence of successive approximations tending to the solution with respect to the metric introduced. The iterations can be obtained from the operator equations as follows:
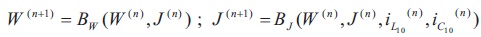
beginning with some initial approximation (W(0), J(0)). It is known that the rate of convergence is

where the contraction constant depends on the parameters of the physical problem. The first approximation can be chosen in various ways, for instance as a solution of the linearized equations of the system. The solution on the interval [L-e, L] can be obtained as in (Angelov, 2016).