Abstract
Let Fn =(M, L) be an n-dimensional Finsler manifold, and Let 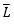
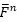
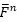
Let Fn =(M, L) be an n-dimensional Finsler manifold, and Let 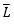
Let Fn =(Mn, L) be a Finsler space, where M is an n-dimensional differentiable manifold equipped with fundamental metric function L. i.e., a Finsler metric on M is a function L=L(x, y) defined as L:TM→[0, ∞) with the following properties:
i) L=L(x, y) is C∞ on TM0,
ii) Lx(y)=L(x, y), is positively 1-homogeneous on the fibres of the tangent bundle TM,
iii) Strong Convex: The n×n Hessian matrix 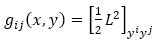
The Finsler space Fn =(Mn, L) is called Finsler space with (α, β)-metric if there exists a 2-homogeneous function L of two variables and such that the Finsler metric F:TM→R is given by F2 (x, y)=L(α(x, y), β(x, y)), where 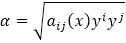
An (α, β)-metric is a Finsler metric expressed in the following form L=αφ(s), s=β/α. The function φ(s) is a C∞ positive function on an open interval (-b0, b0) satisfying
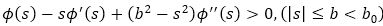
In this case, the fundamental form of the metric tensor induced by L is positive definite.
The tensor 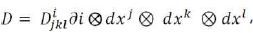

Let Fn =(Mn, L) be an n-dimensional Finsler space on the differentiable manifold Mn, equipped with the fundamental function L(x, y), then β-change of Finsler metric is given by,

where f is positively homogeneous function of degree one in L and β and β given by β(x, y)=bi(x) yi is a one-form on Mn. The Finsler space (Mn, L) obtained from Fn by the β change equation (1) will be denoted by 
Finsler geometry was first introduced locally by Finsler himself (Antonelli, Ingarden, & Matsumoto, 1993), to be studied by many eminent mathematicians for its theoretical importance and applications in the variational calculus, mechanics, and theoretical physics. Moreover, the dependence of the fundamental function L(x, y) on both the positional argument x and directional argument y offers the possibility to use it to describe the anisotropic properties of the physical space.
Bácsó (1997) have introduced the concept of Douglas space, as a generalization of Berwlad space from the view point of geodesic equations. The condition for Finsler space with (α, β)-metric to be of Douglas type was studied by many authors (Li, Shen, & Shen, 2009; Aveesh & Narasimhamurthy, 2013; Park & Choi, 1999; Ramesha & Narasimhamurthy, 2017).
Randers (1941) had considered the simplest possible asymmetrical generalization of a Riemannian metric. Adding a 1-form to the existing Riemannian structure, he was the first to introduce a special Finsler space. This space - which became known in the literature as a Randers space - proved to be mathematically and physically very important. It was one of the first attempts to study a physical theory in the wider context of Finsler geometry, although Randers was not aware that the geometry he used was a special type of Finsler geometry. He has introduced the Finsler change 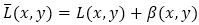

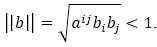
And also In 1984, shibata and his co-authors have dealt with a change of Finsler metric, which is called a β-change of metric (Shibata, Shimada, Azuma, & Yasda, 1977). For a β-change of Finsler metric, the differential one-form β play very important roles.
In (Park & Lee, 2001a) the special Randers changes of Finsler spaces with (α, β)-metrics of Douglas type are characterized. And also (Park & Lee, 2001b), studied the Finsler space with certain (α, β)-metric of Douglas type with Randers change. (Matsumoto, 1974, 1986) had worked on Finsler spaces with Randers metric and special forms of important tensors. And also In 1984, Shibata have studied the general case of any β-change, that is, L=f(L, β) which generalizes many changes in Finsler geometry. In this context, they investigated the change of torsion and curvature tensors corresponding to the above transformation. In addition, they also studied some special Finsler spaces corresponding to specific forms of the function f(L, β).
By studying all these results, in this article, first the authors discuss that the condition for β-change of Finsler space is of Douglas type. Further, In the next part, the conditions for the β-change of Finsler space are derived with different classes of (α, β)- metrics to be of Douglas type.
Let Fn =(Mn, L) be an n-dimensional Finsler space, where Mn be a n-dimensional differentiable manifold and L(x,y) is the fundamental function defined on the manifold TM0 of non zero tangent vectors. It is assumed that L(x, y) is positive and the metric tensors 
The geodesics of an n-dimensional Finsler space Fn =(Mn, L), are given by the system of differential equations: (d2xi)/(dt2)+2Gi(x,dx/dt)=0, where 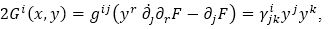
where γjki(x, y) are Christoffel symbols constructed from the Finsler metric tensor gij(x, y) with respect to (xi).
The covariant differentiation with respect to Levi-Civita connection {γjki} of Rn is denoted by (;).
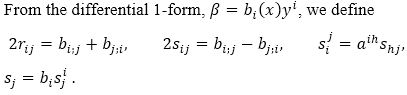
A Finsler space Fn is said to be Douglas space, if
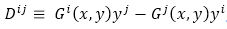
are homogeneous polynomial in (y) of degree 3.
According to Basco (1997), a Finsler space Fn is of Douglas type if and only if the Douglas tensor 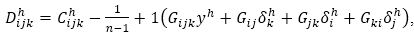
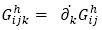
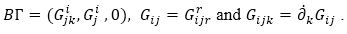
According to (Matsumoto, 1998a), the function Gi (x, y) of Fn with the (α, β)-metric are written in the form,
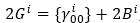
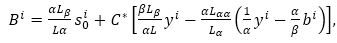
where 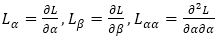
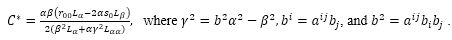
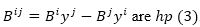
Since are homogeneous polynomial in (yi) of degree two.
From equations (3) and (5), we have
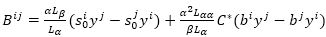
Thus, the condition for a Finsler space to be of Douglas Space is that are hp(3)
Let 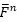
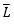
From equation (6), 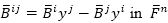
are written as
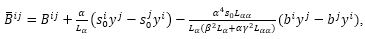
Suppose Fn is a Douglas space. Since Bij are hp(3), the necessary and sufficient condition for Fn to be also a Douglas space is that
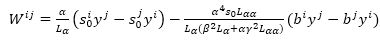
are homogeneous polynomial of degree 3.
We use the results proved by Park and Lee (2001b)
Let Fn =(Mn, L), be a Finsler space with an (α, β)-metric of Douglas type. Then Fn =(Mn, L+β) which is obtained by a β-change of Fn is also a Douglas space if and only if Wij is homogeneous polynomial of degree 3.
i.e., Suppose Fn is a Douglas space. The condition for Fn =(Mn, L+β) to be a Douglas space is that equation (8) is hp (3).
In this section, the condition for a β-change of Finsler space Fn is found to be of Douglas type.
Let us denote the following notations:
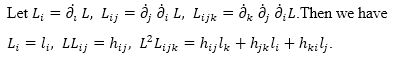
And again 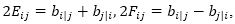
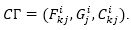
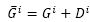
Then 
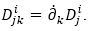
and
. The tensors
Di, Dji,Djki and
are positively homogeneous in yi of degree two, one, and zero, respectively. In the following, the explicit form of Di is necessary. To find this, we deal with equation Lij|k =0, where Lij|k is the h-covarient derivative of Lij=hij/L in CΓ. Then
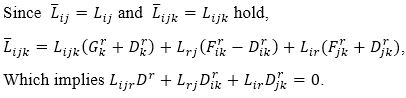
Transvecting equation (10) by yk, we have
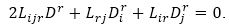
Again consider Li|j =0, then
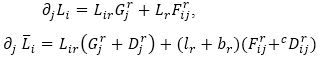
Where
Plugging equation (12) in 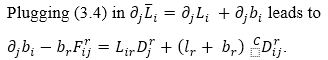
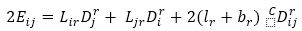
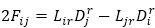
From equations (11) and (14) , we have

Contracting equation (13) by y which yields

Again contracting equations (15) and (16) by yi leads to

which represents the system for linear equations.
Here we use the following lemma proved by (Matsumoto, 1998b),
A system of linear equations 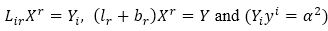
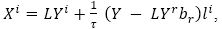
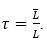
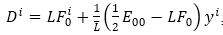
where Fji =gir Frj and Fj=brFjr.
Therefore, the tensor Di of (9) arising from a β-change are given by (18).
Again from equations (9) and (18), we have
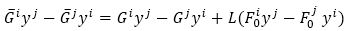
Suppose Fn is a Douglas space, that is, Giyj-Gjyj are hp (3). Thus we have
Proposition 1: Let Fn be a Douglas space and Fn a Finsler space which is obtained by a β-change by β. is also a Douglas space if and only if 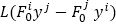
Let Fn =(Mn, L), be a Finsler space. And be a Finsler space, which is transformed by a β-change of Finsler space Fn =(Mn, L) is of Douglas type.
Here we are discussing three different classes of (α, β)-metrics, which is transformed by a β-change of Finsler space Fn =(Mn, L),
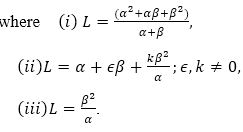
are of Douglas types
 is of Douglas Type
is of Douglas TypeIn this section, the authors characterize the condition for a Finsler space 

For an (a, b)-metric,
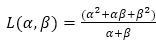
The partial derivatives of equation (18) are as follows:

For 
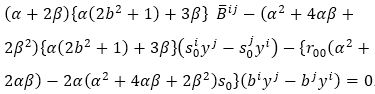
Suppose that 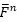


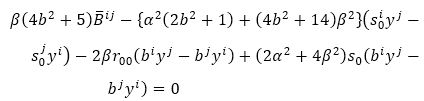
Eliminating from equations (23) and (24), which yields,

where,
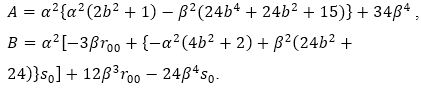
Contracting equation (25) by biyi, which yields
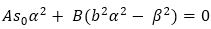
Since the term 12β5 (2βs0 -r00) of (26) seemingly does not contain α2, thus we must have hp(5) v5, such that
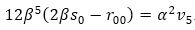
Let us study the following cases.

Now the terms is equation (26) can be written as,
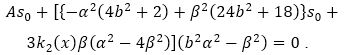
The terms in equation (28) does not contain α2 as a factor are 
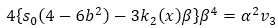
From α2(mod β), then v3 vanishes and

Contract equation (30) by bi, which yields k2b2 =0.
If k2 =0, then b2 =2/3 or si=0.
Again if b2 =2/3, the terms of equation (28) can be written as 3α2 (7 α2-33β2) s0 =0, which yields s0 =0 and r00 =0.
Next, if si=0, then we have s0 =0 and r00 =0.
On the other hand, if b2 =0, terms of equation (28) can be written as,

which implies s0 =0 and k2 =0.
Therefore, for n>2, in both the cases of v5 =0 and v5 ≠0 leads to r00 =0 and s0 =0. So that equation (25) can be written as,
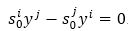
Contract equation (31) by yi gives s0i =0. Since rij =sij =sji =0, we conclude that bij =0.
Thus, we state that,
Theorem
A Finsler space 
 is of Douglas Type:
is of Douglas Type:Let us consider an (α, β)-metric

And partial derivatives of equation (20) are:

To deduce the condition for Finsler space , which is obtained by a β-change of Fn =(Mn,L), using equation (34) in (7) yields
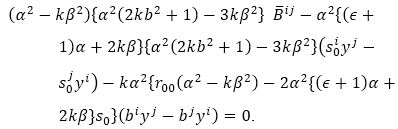
Suppose be a Douglas space, that is,
be homogeneous polynomial in (y) of degree 3. Since α is irrational in (yi), the terms of equation (35) can be divided in two equations:
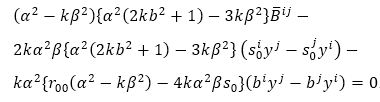

Transvecting equation (37) by biyi, which yields

From equation (38), s0α2=0⟹si=0.
∴ equation (37) reduces to
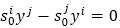
Transvect equation (39) by yi yields s0i=0 immediately after sij =0. Again, put equation (37) in (36), we have
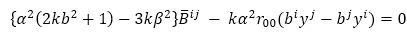
In equation (40), only the term [3kb ] does not contain α2 as a factor, thus we must havehp(3) v3ij ;
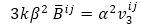
If suppose α2 ≢0(modβ). Then equation (41) is reduced to
" style="vertical-align: bottom; display: inline;" width="" /> where vij are hp(1). Thus equation (40) leads to
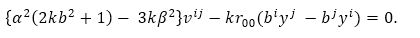
Transvecting equation (42) by biyj, we get

Now we define a function f1 (x);
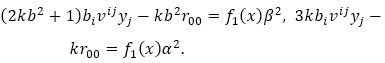
Removing bi vij yj from equation (44), which yields
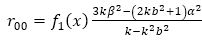
∴from equation (45) and sij =0, which yields
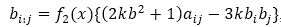
where,
Conversely, if equation (46) is holds good, then sij =0 and
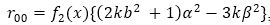
then 
Now, we define,
Theorem
Let Fn=(Mn, L) Finsler space with an (α, β)-metric L=α+ϵβ+k β2/α; ϵ, k≠0. A Finsler space 
where
 is of Douglas Type
is of Douglas TypeLet us consider an (α,β)-metric,
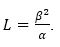
partial derivatives of equation (48) are:
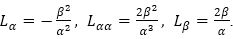
To prove 
Using equation (48) in (7) which yields

If 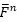

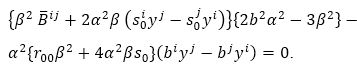
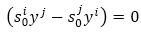
Transvecting equation (52) by biyj, which yields,
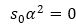
From equation (43), we have s0 =0⟹si=0.
∴ equation (52) becomes
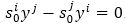
Transvecting equation (50) by yi yields s0i =0⟹sij =0.
Again, by using equation (52) and s0 =0 in (51), we have
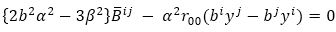
In equation (55), it seems that only the term does not contain α2, thus we must have hp(3) v3ij, such that
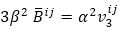
If α2 ≢0(modβ). Then equation (56) is reduced to where vij are hp(1). Thus equation (55) leads to
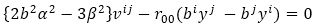
Transvecting equation (57) by biyi, we get

Now we define a function f1 (x);
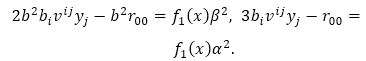
Removing bi vij yj from equation (59), which yields
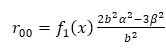
∴ From equation (60) and sij =0, which yields
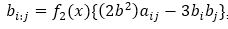
where, f2(x)= f1(x)/ b2
Conversely, if equation (61) is holds good, then sij =0 and
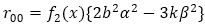
then 
Thus, we define,
Theorem Let Fn =(Mn, L) Finsler space with an (α, β)-metric L=β2 /α. A Finsler space 
where f2(x) = (f1(x))/b2.
The theory of Finsler space with (α,β)-metric has been developed into faithful branch of Finsler Geometry. From stand point of Finsler Geometry itself, Randers metric is very interesting because its form of simple and properties of Finsler spaces equipped this metric can be looked asRiemannian spaces equipped with the metric L(α, β) = α + β.
With this M, Matsumoto introduced the transformation of Finsler metric (x, y)=L(x, y)+β(x, y) where β(x, y)=bi(x) yi is a one-form.C. Shibata introduced thetransformation of Finsler metric (x, y)=f (L, β),where β(x, y)=bi(x) yi, bi(x) are components of a covariant vector in (Mn, L)and f is positively homogenous function of degree one in L and β.
And also G. Randers studied the properties of β-change.
By studying all these concepts, the authors have finally summarized the results as follows:
In the first part, it deals with the β-change of a Finsler space with the (α,β)-metric is of Douglas type. Further, the Finsler space n n is investigated, which is transformed by a β-change of a Finsler space Fn =(Mn,L)with different classes of (α,β)-metrics is of Douglas type and vice versa. In this regard, the following conclusions are arrived.
A Finsler space 
A Finsler space 
bi:j = f2 (x){(2kb2+1) aij -3kbi bj},
where f2(x)=(f1(x))/(k2b2 -k).
A Finsler space 
The authors confirm that there is no conflict of interest to declare for this publication.
The authors would like to appreciate the effort from editors and reviewers. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.