(1)
The Maxwell model is considered to be the simplest of rate type fluids model of viscoelastic fluid, the model describes the blood flow in small vessels. And also the response of some polymeric liquids. The focus of this work is derivation of magneto-hydrodynamic of Maxwell model in cylindrical co-ordinates (r, θ z), basic equations (equation of continuity and momentum), and the Maxwell model were changed from the vector form to deferential form to derive the model in cylindrical co-ordinates (r, θ, z). The Maxwell equation has been derived and system of partial differential equations was obtained under effect of magnetic field.
The Maxwell model is the simplest subclass of rate type fluids model of viscoelastic fluid. In recent year, this model has had some success in describing the response of some polymeric liquids (Fetecan Athar & Fetecan, 2009). The Maxwell model can predict the stress relaxation and therefore, have become more popular. It has been applied to problems having small vessels by using the viscoelastic Maxwell model.
Most of the investigations in the literature have been carried out by considering blood, physiological fluids, oils, etc., as Newtonian fluids. This approach (considering blood, physiological fluids, and oils as Newtonian fluids) may provide satisfactory understanding of peristaltic mechanism in the ureter, but it fails to give a better understanding when involves small blood vessels, lymphatic vessels, intestine, ductus and efferent of male reproductive tracts, transport of spermatozoa, oils and hydrocarbons (Ibrahim, 2013).
The Magneto-hydrodynamic (MHD) (Alfvén, 1942) peristaltic flowing of a fluid is in problems involving blood and blood pump machine. The influence of magnetic field may be utilized as a blood pump for blood flow in arterial stenosis or arteriosclerosis (Ibrahim, 2013). To drive the model in cylindrical co-ordinates, firstly we change the basic equations and the Maxwell model from vector form to deferential form and represent them in matrices to extract system of partial deferential equations.
The continuity equation is an equation that describes the transport of some quantity; continuity equation is simply a mathematical expression of conservation of mass. The continuity equation of incompressible flow (Pedlosky, 1987) in vector form is given by,
where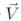 
is the velocity components vector.
Equation (1) can be expressed in cylindrical coordinates (r, θ, z)
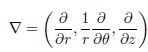
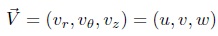
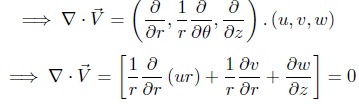
The momentum equation is a statement of Newton’s second law and relates the sum of the forces acting on an element of fluid to its acceleration or rate of change of momentum. And the equation momentum is relating acceleration to the force at a point and holds fo any continuum, solid or fluid, no matter how the stress tensor is related to the deformation field (Kundo & Cohen, 2008)
The expression of momentum equation of incompressible fluid in the vector form is:
where, ρ is density, t is time, τ is the stress tensor, 
is current density and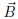 
is the magnetic field.
1.2.1 Material Derivative
The material derivative (Batchelor, 2000; Bird, Stewart, & Lightfoot, 2007) describes the time rate of change physical quantity (like momentum) of a material element is subjected to a space and time dependent macroscopic velocity field variations of that physical quantity. For any continuum, forces acting on a piece of material are of two types. First, there are forces of stress, where by the piece of material is acted on by forces across its surface by the rest of the continuum. Second, there are external, or body forces such as gravity or a magnetic field, which exert a force per unit volume on the continuum. The expression below shows the material derivative in vector form.
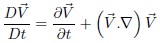
where:
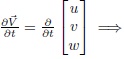
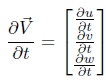
and
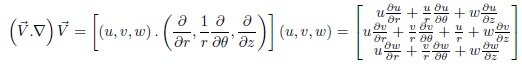
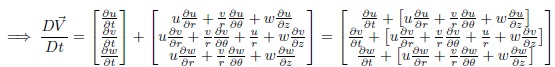
Cauchy stress tensor, true stress tensor (Irgens, 2008), simply called the stress tensor is used to model the part of the point within some material that can be attributed to the strain rate, the rate at which it is deforming around that point. Cauchy stress tensor is formally similar to the elastic stress tensor that describes internal forces in an elastic material due to its deformation (Landau & Lifshitz, 1997). In viscoelastic materials, whose behaviour is intermediate between those of liquids and solids, the total stress tensor comprises both viscous and elastic (”static”) components. For a completely fluid material, the elastic term reduces to the hydrostatic pressure. Cauchy stress tensor in cylindrical (r, q, z) can be represented by 3 x 3 matrices in equation (11), and below equation is Cauchy stress tensor in vector form.
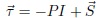
where, P is the pressure, I is the identity tensor, and is the extra stress tensor.
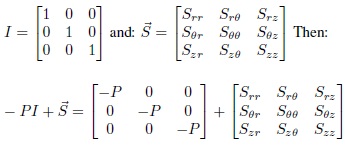
Equation (10) becomes
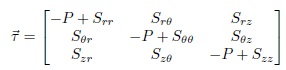
Then,
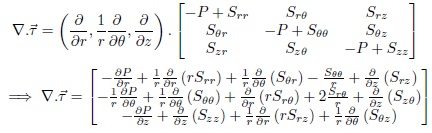
And the expression 
is the Lorentz force (magneto-hydrodynamic) in cylindrical coordinates (Ibrahim, 2013; Zakaria & Amin, 2013).
Magneto-hydrodynamics is the study of the behaviour of an electrically conducting fluid in the presence of a magnetic field. The equations of magneto-hydrodynamic are the usual electromagnetic and hydrodynamics equations, modified to take account of the interaction between the motion and the magnetic field. By substituting equations (9), (11) and the Lorentz force (magneto-hydrodynamic) into equation of momentum (5) to obtain the following equation:
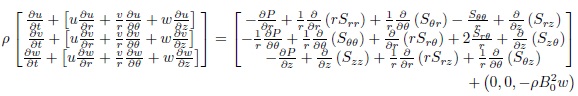
From equation (12), we obtain system of partial deferential equations of momentum equation:
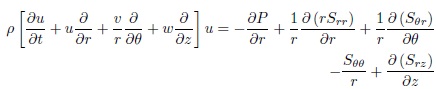
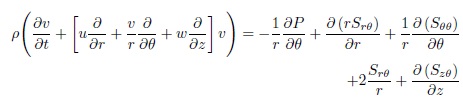
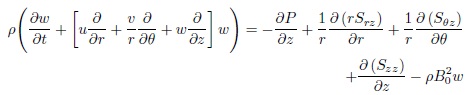
Maxwell’s equations are a set of partial differential equations that, together with the Lorentz force law. Maxwell’s equations describe how electric and magnetic fields are generated (Griffiths, 1999). The Maxwell constitutive equation is given by:
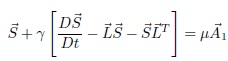
Where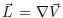 
is the velocity gradient, γ is the extra stress tensor, 
is the time relaxation, and A1 is the first Rivlin-Ericksen tensor.
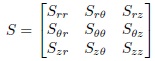
1.4.1 Material Derivative
where
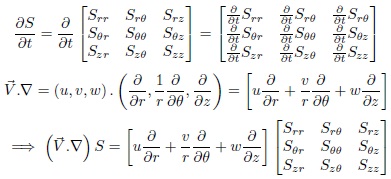
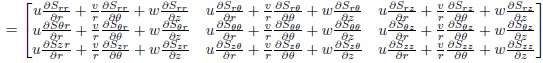
By substituting equations (19) and (20) into the material derivative, equation (17) to obtain:
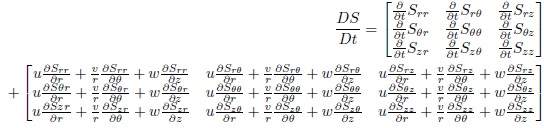
And the velocity gradient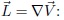 
where:
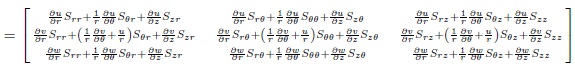
and
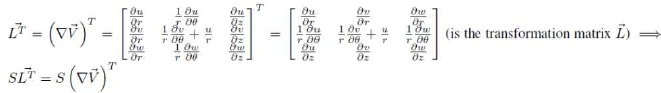
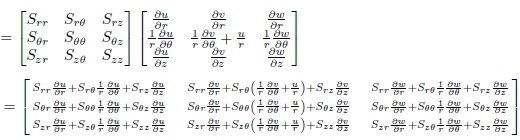
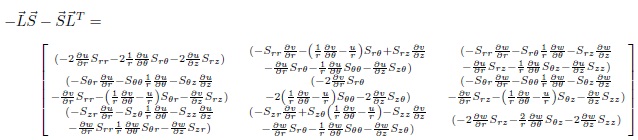
1.4.2 First Rivlin-Ericksen Tensor
The first Rivlin-Erickson tensor is denoted by A1 and its temporal evolution of the strain rate tensor such that the derivative translates and rotates with the flow field (Truesdell, & Noll, & walter, 2004) defined by:
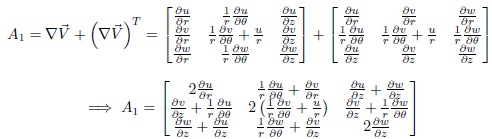
By substituting equations [(21)-(24)] into Maxwell constitutive equation (17), we obtain:
From equation (25) we obtain the following system of partial deferential equations,
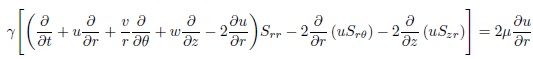
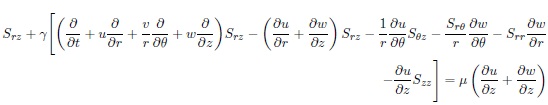
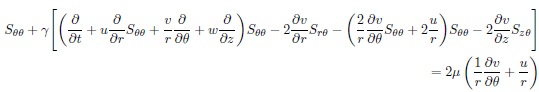
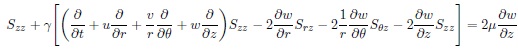
The continuity and momentum equations in (1) and (2), respectively have been derived in cylindrical co-ordinates in equation (4) and [(13) - (15)], respectively. And also the magneto-hydrodynamic of Maxwell model has been derived in cylindrical co-ordinates (r, θ, z) and system of partial differential equations were obtained in equations [(26) - (30)] respectively under the effect of magnetic field.