
Although remarkable progress has been made in the control of the global Human Immunodeficiency Virus (HIV/AIDS) epidemic, the burden of HIV has reached contemporary at the shocking level in Sub-Saharan Africa. Understanding the cycle of HIV/AIDS disease progression can have great value on the effectiveness of the therapy. The purpose of this study is to determine factors affecting the progression between different stages of the disease and to model the progression of HIV/AIDS disease of HIV infected patients under ART follow-up using multistate Semi-Markov model. A cohort of 526 HIV infected patients has been sampled from a Hawassa University Referral Hospital, Hawassa, Ethiopia, who have been under ART follow up from September 2012 to August 2017. States of the Markovian process are defined by the seriousness of the sickness based on the CD4 counts in cells/microliter. The five states of HIV/AIDS disease progression considered in the multi-state Semi-Markov model were defined based on of the following CD4 cell counts. State I, State II, State III, State IV, and Death state. The major transiently prognostic factors between different states of HIV/AIDS disease were sex, age, ART adherence level, TB status, functional status, opportunistic infections ,and body weight of patients. Hence, the progression of HIV/AIDS was significantly accelerated with poor ART adherence, patient's co-infection with TB, older patients, and patients being bedridden. The conditional probabilities of patients from any good states to worst state are increasing over time. Weibull sojourn time distribution is the appropriate and is preferably used as sojourn time distribution under multistate models. As time elapsed, the transition probability of patients is more likely to be in worse state than to be in better one. This shows that patients should aware the need to initiate therapy at early stages of the virus.
Globally, the diffusion rate of the HIV/AIDS has reached contemporary at shocking level. The AIDS epidemic is one of the most obstructive chronic diseases in the history of humankind, claiming the lives of people (Desalegn, 2016). That disease has been first recognized as a new disease in 1981, when increasing numbers of young homosexual men succumbed to unusual opportunistic infections (Sharp & Hahn, 2011). Its virus spreading it, HIV, was discovered in 1983 and then, by 1990 epidemics were recorded in nearly all countries in the world (Egerö & Hammarskjöld, 2000). It is primarily a sexually transmitted disease (Sharp & Hahn, 2011).
As to the global prevalence of HIV/AIDS is concerned, by June 2017, it was estimated that there were an estimated 36.7 million peoples living with HIV/AIDS (PLWHA), of which approximately 1 million people died from AIDS-related illnesses in 2016. The report underlines, the overwhelming estimated a majority of about 25.8 million people living with HIV/AIDS and about 740,000 people died from AIDS in 2016 were from developing countries basically with the highest prevalence rates recorded in young adults in Sub-Saharan Africa (UNAIDS, 2017).
With a population of over 95 million, Ethiopia is the second most populous country (next to Nigeria) in Sub-Saharan Africa. Ethiopia has some of the highest rates of HIV/AIDS in the world. The first time that HIV observed in Ethiopia was in 1984 and the first two AIDS cases were reported in 1986. Then, National AIDS Control Program (NACP) was established at the department level at the Ministry of Health (MoH) in 1987 (Desalegn, 2016). HIV in Ethiopia has beat down consequences that inevitably compromise, where it affects the economic development of the country (FDRE, 2014). Now a time HIV/AIDS, is the greatest public health challenge facing Ethiopia. According the report of (UNAIDS, 2017) in Ethiopia there were an estimated 7,10,000 people living with HIV and approximately 20,000 deaths were related to AIDS in 2016. More than 6,39,000 of these are adults making Ethiopia in the list of the largest African population of people living with HIV.
According to national report of PEPFAR, (2016) in Ethiopia, the over-whelming estimated majority regions of AIDS prevalence covers in Addis Ababa, Amhara, Oromia, and SNNPR account for 93.4% of the total PLHIV in the country.
AIDS could lead to death by reducing a person's ability to fight infection. HIV attacks an immune cell called the CD4+ T-lymphocyte, which is the number of CD4 cells per micro liter of blood. The CD4 cell count is an important biomarker in providing information about the progression of AIDS disease among HIV/AIDS infected patients. It plays a crucial role in the immune system, whereas when an individual loses CD4 cells, he or she is more vulnerable to opportunistic infections and lymphomas. CD4 count is often measured repeatedly over subsequent follow-up period in the ART treatment services. Describing the evolution of CD4 cell counts over time for patients on ART follow-up treatment is useful to show the progression of AIDS disease (Asena & Goshu, 2017; Dinberu, Kibralem, Sisay, & Mulualem, 2016; Grover, Gadpayle, Swain, & Deka, 2013; Reddy, 2011).
Moreover, Mwambura and Samuel reported that CD4 cell count has been an important factor in the clinical investigation of HIV patients as well used as prognostic marker for assessing HIV progression. The CD4 counts have been used as an indicator of ART initiation. The ART should start when CD4 count is below 350 cells/microliter. When an individual loses CD4 cells he or she is more vulnerable to opportunistic infections (Mwambura & Samuel, 2017). In this study, a model with state structure based on intervals of CD4 count and death as an absorbing state was used. Accordingly, the perceptive of HIV progression can have great value on the development of new treatment strategies (Reddy, 2011).
Although remarkable progress has been made in the control of the global HIV/AIDS epidemic, the burden of HIV is still severe in Sub-Saharan Africa. In that sense, understanding the natural disease process of HIV/AIDS progression and exploring determinant factors that influence the disease progression to accelerate or decelerate can have great value on the development of new treatment strategies (Reddy, 2011).
Most of the time in medical investigations, survival analysis is a well developed statistical method, which explores time to single event analysis. However, such methods may not sufficiently confine the process of any disease as the progression of disease may occupy intermediate events of interest. Thus, multistate models best incorporate multiple events or states (Reddy, 2011). Inline to this, for longitudinal chronic disease studies with categorical response variables, the natural development of a chronic disease is often expressed in terms of different states and multistate models are widely used to model the progression of individuals through these states (Goshu & Dessie, 2013).
Few studies have been conducted to study HIV/AIDS disease progression using the CD4 count measurements, including both the concept of survival and stochastic effect in Ethiopia. Goshu and Dessie aimed to model the progression of HIV/AIDS disease of an individual patient under ART follow-up using Time Homogeneous semi-Markov processes (Goshu & Dessie, 2013). They mainly focused the transition probability of different states. Quite another, Goshu and Asena have applied Semi-Markov models to the HIV/AIDS disease progression and compared two sojourn time distributions, namely exponential and Weibull probability distributions. They reported that Weibull distribution is flexible in modeling and it can preferably be used as waiting time distribution under Semi-Markov modeling and monitoring HIV/AIDS disease progression over time (Goshu & Asena, 2017).
Moreover, Dinberu et al. (2016) focused on the prediction of the evolution of CD4 count in time using a stochastic model, discrete time Semi-markov chain model, on longitudinal data from south west Ethiopia. They resulted, the probability of staying at the starting CD4 count state was decreased, when time increased, patients from the state I has higher probability to remain in the ART starting state (Dinberu et al., 2016). Quite another, Desalegn proposed to apply the Cox proportional hazard model to review the determinant factors of survival time and discrete time homogeneous Semi-Markov model to predict the clinical progression of AIDS disease (Desalegn, 2016).
However, studies have been done on ADIS disease progression to model the CD4 counts of HIV/AIDS patients, the effect of cofactors for people living with HIV/AIDS on progression of HIV/AIDS disease and the length of stay with different CD4 count stages is not well studied yet. Studies, which deal with those issues contribute in strengthening the implementation of ART.
Therefore, this study aims to fill this literature gap as well to model HIV/AIDS disease progression and determinant cofactors that affect the transition between different states of chronicity among 526 HIV/AIDS patients receiving ART through the application of multistate Semi-Markov Process (SMP) in the case of Hawassa University Referral Hospital.
Hence, the study is motivated to identify the major risk factors associated with HIV/AIDS disease progression, which are also common to a number of other chronic diseases. Efforts have been made to answer the crucial questions that are remained unanswered regarding clinical progression of HIV/AIDS disease.
1. Which risk factors significantly accelerate or decelerate the progression of HIV/AIDS disease?
2. What is the conditional probability of HIV/AIDS patients to be in different state transitions at a given time?
3. Which sojourn time distribution is appropriate to monitor HIV/AIDS disease progression over time?
The general objective of the study is to assess factors affecting to accelerate or decelerate the progression between different stages of HIV/AIDS disease using multistate Semi-Markov models.
1. To estimate the conditional probability of State Transition of sojourn time Hazard rates of the Semi-Markov Process to predict life time of patients.
2. To identify the appropriate sojourn time distributions for monitoring HIV/AIDS disease progression over time under multistate Semi-Markov model.
The study was carried out in Hawassa University Referral Hospital, which is the Comprehensive Specialized Hospital found in Hawassa city, Ethiopia. The data for this study was from retrospective follow up data in which the CD4 cell count of subsequent patients has been recorded longitudinally. Each patient is codified and the following data are available: Patient Identifier (ID), patient age (in years) during enrollment, the functional status of patients in their subsequent follow up, date of enrolment into the cohort, gender, past opportunistic infection, date of seroconversion, date of ART therapy initiation, TB diagnosis, date of last clinic visit, date last alive, date of death, date of CD4 count measured, experimental value of CD4 count (cells/microliter), body weight of a patient during his\her visit, and patients' ART adherence level. The clinical measurements for each subject are scheduled approximately every six months. Some additional measurements are also performed whenever the patient's state worsens. The data on CD4 counts of HIV/AIDS patients who took at least two visits on follow-up throughout 2012-2017 was obtained from Hawassa University Referral Hospital, Ethiopia.
The authors have categorized four (good) states of the Markov process of the seriousness of HIV/AIDS sickness based on the CD4+ T-lymphocyte counts per microliter of blood as follows: State I : (CD+ count > 500 cells/microliter), State II: (350 cells/microliter < CD+count ≤ 500 cells/microliter), State III: (200 cells/microliter < CD+count ≤ 350 cells/microliter), State IV: (CD+count ≤ 200 cells/microliter). An absorbing (bad) state D is added corresponding to the death of the patient. The good states indicates that the patient is alive, whereas the bad state indicates that once a patient is in the death state, she/he can never be in the other states and rather stays there forever.
This study considered a retrospective cohort of all HIV/AIDS patients under follow up of ART treatment whose ages were greater than 15 years at Hawassa University Referral Hospital, from September 2012 to August 2017. The data on CD4 counts of HIV/AIDS patients who took at least two visits on follow-up throughout 2012-2017 was considered.
Sampling technique is a system of taking small ratio of observation from large population to get information of that large population from the sampled observation by using the same statistical techniques.
3.1.1 Sampling Design
Retrospective cohort study has been done on patients, who were under the subsequent follow up of ART at Hawassa University Referral hospital between September 2012 and August 2017.
Simple Random Sampling (SRS) is one of the basic probability selection schemes in which a predetermined number of units from a population list are selected, so that each unit on that list has an equal chance of being included in the sample. In this study, the documented lists of those who started the ART in Hawassa University Referral Hospital who have a unique identification number are considered as sampling frame. A simple random sampling procedure is applied.
3.1.2 Sample Size Determination
In conducting research that requires taking a sample, we always have the stages of making a decision of the sample size. Making a decision is helpful that taking too large sample implies a waste of resources, while too small sample reduces the usefulness of the result. In order to have an optimum sample size, there are a number of assumptions a researcher has to take it into account. Some of the issues are like: objective of the research, cost constraint, plan for statistical analysis, and degree of precision required for generalization.
Based on the above assumptions, this research employed the appropriate one, which satisfied the research objectives. The adopted sample size determination formula (Cochran, 1977) for this research was,

If 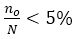
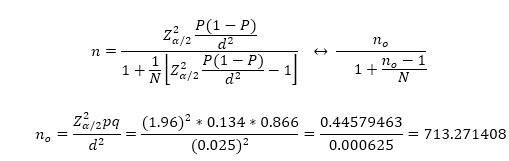
Now, 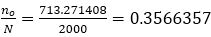
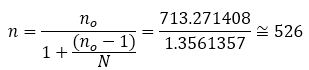
where, Z α/2 is the upper 2α points of standard normal distribution with α=0.05 significance level, which is Zα/2=1.96. “d” is the a degree of precision that is mostly selected by the investigators. The term p represents proportion of death among HIV/AIDS patients It was obtained from the previous comparable study done by (Asena & Goshu, 2017) on data taken from Yirgalem General Hospital, which is p=0.134. The degree of precision d selected for this study was 0.025. Hence, among 2000 adult HIV/AIDS patients in Hawassa University Referral Hospital about 526 patients were included in the study according to the sample size determination formula in equation (2).
The variables we consider in this study were selected based on related literatures. However, none of the studies that used multi-state Semi-Markov approaches to model HIV/AIDS progression investigated patient's opportunistic infection, body weight, and functional status.
3.2.1 Response Variable
The states of disease progression adopted the time lapse between state transitions was determined using the difference (in months) between the dates of CD4 tests. Thus, the main response variable is the change in CD4 cell lymphocyte level of patients in an interval of six months since enrolment on ART and absorbing state (i.e.: State I, State II, State III, State IV, and death).
3.2.2 Predictor (Explanatory) Variables
The explanatory variables that may have influence on the prediction of the response variable were Sex, Age, body weight, Patient's Functional status, ART adherence level of patients, Patient TB Screen, and past opportunistic infection.
In this study, homogeneous multisate semi-markov model was adopted for predicting the clinical progression of HIV/AIDS disease and the survival probability of HIV infected patient up to specified t month.
Dinberu et al. (2016) examined that the immunological assessment using the CD4 count identifies the disease progression and determines initiation of treatment. In addition to this, CD4 testing can monitor the ART response as well in adult and adolescence, the WHO guidelines recommend that ART be initiated in patients with history of an AIDS defining illness (Stage IV).
Compared to different types of multistate models used in biomedical sciences, fewer and less rigid working hypotheses are needed, a large number of disease states can be considered, all the states might be interrelated, therefore any improvement is also considered; the model needs raw data obtained from observations, without strong assumptions about any standard probability functions regarding the random variables analyzed. Moreover, this study investigates the survival probability of patients using the probability of transition from one WHO stage to another depending on the current state and the sojourn (time elapsed) in the current state. Hence, the results are often very useful for physicians for making decisions on the prediction of clinical progression of HIV/AIDS disease.
Let us consider a Markov process (Jn,Tn)nϵℕ , where T0 < T1< ....< Tn < ∞ are the successive times of entry to states J0< J1<....

Let N(t)=sup{nϵℕ:Tn ≤ t, tϵℝ+} be the counting process, which counts the total number of observed transitions during the time interval [0, t]. The process JN(t), which represents the state of the process at time t, defines a homogeneous Semi-Markov process. The probability distribution function of sojourn time is related to the Semi-Markov kernel through the transition probabilites of embeded markov chain (Krol & Saint-Pierre, 2015)
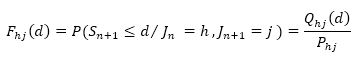
Let us suppose that the survival function Ghj(.), the density function fhj(.), and the hazard rate αhj(.)associated to this probability distribution can be defined. The survival function of Sojourn time in state h is defined by,
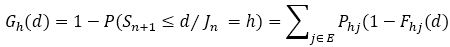
The hazard rate of the Semi-Markov process corresponds to the probability of transition towards state j between time d and d+Δd, given the process is in state h for a duration d (Krol & Saint-Pierre, 2015).
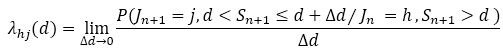
The hazard of the Semi-Markov process is related to the hazard rate of the sojourn time, the survival functions of the sojourn times, and the transition probabilities of the Markov chain by the following relation (Krol & Saint-Pierre, 2015).

Suppose that the waiting time in a given state is random and have a distribution. It is assumed that process spends some time in a given state and random time has distribution G(t). The following sojourn time distributions were considered for modeling progression of HIV/AIDS disease.
3.5.1 Exponential Distribution
In exponential distribution, the hazard function is constant (corresponding to the Markov case).

where, 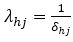
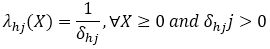
3.5.2 Weibull Distribution
The sojourn time in Weibull distribution is given as,
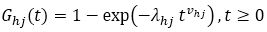
The Weibull distribution, which generalizes the exponential one, is often used in practical applications. Indeed, the Weibull distribution with two parameters (δhj, vhj) is well adapted to deal with various shapes of monotone hazards, where, δhj>0 is a scale parameter and shape parameter vhj >0. The hazard function of Weibull distribution is defined as,
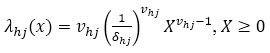
3.5.3 Comparison of the Sojourn Time Distributions
There are several methods of model selection. One way to evaluate a model is to use the Akaike Information Criterion (AIC). This criterion attempts to quantify how well the model has predicted the data. The Akaike's Information Criterion (AIC) is a useful statistic for comparing the relative fit of different models. This statistic is given by:

where, k is the number of parameters in the model. This method penalizes the log likelihood for the number of parameters estimated. The model with the smallest AIC value is considered as a better fit. Alternatively, Bayesian Information Criterion (Foucher, Mathieu, Saint-Pierre, Durand, & Daurés, 2005) is used to compare models and similarly model with the smallest BIC value is considered as a better fit and it is given by,
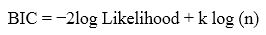
3.6.1 Parametric Maximum Likelihood Estimation
In a parametric framework, distributions of sojourn times are supposed to belong to a class of parametric functions. For each transition, the distribution (which depends on a finite number of parameters) can be specified using either the hazard rate αhj(,), the density fhj(,), or the cumulative distribution function Fhj (,).
The likelihood function associated with a single Semi-Markov process can be written as (Krol & Saint-Pierre, 2015),
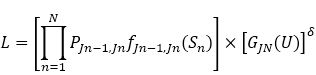
where, N is the total number of observed transitions between two states, U denotes the duration between the time of the last observation, and TN is the time of the end of the study. The indicator δ is equal to 1 if the last sojourn time U is right censored by the end of the study indeed; the last duration and the last arrival state are unknown unless the process entered an absorbing state (δ=0). When an observation is right-censored (δ=1).
The survival function of the sojourn times is taken into account. The first part of Equation (12) involves the density function and the probabilities of the Markov chain; it corresponds to the contribution of the observed transitions. The full likelihood L is the product of all individual likelihood contributions.
The study sample was obtained from a total population of 2000 HIV/AIDS patients, where among these a random sample of 526 patients (200 Male, 326 Female) was taken. 69.39% of them are patients aged between 15-35 years old and from the Descriptive characteristics of subjects Table 1 we see that the number of females participated in the study exceeded the number of males, which is 61.98% of the total number of patients are female. Table 1 describes that 14.26% deaths occurred at the end of the study period and about 85.74% of patients accounted as censored observations. Since, the study is part of continuing follow up patients may survive beyond the study period, lost to follow up, and the observations follow right censoring mechanism. The functional status of HIV infected patients who were Bedridden, Ambulatory, and working status was 6, 81, and 439, respectively. Initial information of patients (like CD4 count, body weight, TB status) were taken every six months.
The result in Table 2 indicates Transition Probability Matrix of patients in each Stage (Stage I, Stage II, Stage III, and Stage IV). The probability of death in Stage I, Stage II, Stage III, and Stage IV are 0.0259, 0.0203, 0.0422, and 0.0991, respectively. The Table also shows that a patient from State I, State II, and State III enters to the fourth disease stage (i.e.: State IV) with the probability of 0.0189, 0.0778, and 0.0864, respectively this result describes the probability of patients developing AIDS disease gets increased as the CD4 count gets declined or smaller. Moreover, the recovery probability of patients from State IV to State III, State II and State I was 0.4257, 0.3036, and 0.0891, respectively. Patients show recovery from State IV to State III, from State III to State II, and from State II to State I with probability 0.4257, 0.5086, and 0.4721, respectively.
Table 2. Estimates of the Transition Probability Matrix of the Embedded Markov Chain (Hawassa University Referral Hospital, 2012-2017)
More precisely, the probability of patients moving to a better state is higher than the probability of moving to a worse state. For instance, patients with CD4 count less than 200 (for particular patient in state IV), where the probability of moving to state III (recovery) is 0.4257, which is very high as compared to probability of making a jump to the worst state (death).
The investigation on disease progression has further been extended by including covariates, such as sex, age, opportunistic infection, weight, functional status, ART adherence, and TB status, using generalized hazard regression modeling. Timeindependent and time dependent covariates were included. Final model has been selected on the basis of the Likelihood Ratio (LR) test.
Table 3 presents 7 covariates with 27 regression coefficients. For each estimation of regression coefficients with the hypothesis of interest are given as: H0: βk,hj =0, where "k=1, 2,…, 7" is the label of cofactors (i.e. 1 for sex, 2 for weight, 3 for Age, 4 for TB status, 5 for functional status, 6 for ART adherence, and 7 for opportunistic infection), hϵ{I, II, III, IV} and jϵ{I, II, III, IV, D}. The Semi-Markov Hazard Ratios (HR) of co-factors (i.e. Sex, Age, Weight, Opportunistic infection, Functional status, ART adherence, and TB status) on each transition along with 95% CI was interpreted as follows:
Table 3. Estimates of Hazard Ratios (95% CI) for State Transitions from Multivariable Cox Ph Model in Patients Diagnosed with AIDS under ART, Hawassa University Referral Hospital using Semi-Markov Model
The transition found to be significant with female patients from State I to State II, State I to State III, State I to State D, State II to State I, and State IV to State I, Which indicates that female patients were about 1.42 times more likely to move from State I to State II than those of male patients (HR = 1.4205, CI = 1.041-1.954). More precisely, the estimate of the coefficient affected to the transition from State I to State II is significantly different from 0 (β1,12= 0.351; p = 0.029). It means that female patients increase the risk of leaving State I to enter State II. Correspondingly, female patients were 2.77 times more likely to move from State I to State III than those of male patients (HR = 2.77, CI = 1.27-6.049), which means that women are predisposed to move quickly from State I to State III with the estimate of the coefficient related to the transition from State I to State III is significantly different from 0 (β1,13= 1.02; p = 0.0104). However, the HR=0.15 in the transition of (State I→D State) for female patients was at the risk of moving from State I to Death state. That indicates, female patients who had been at State I are dying at a rate, which is 85% lower than male patients with the estimate of the coefficient associated to the transition from State I to State D is significantly different from 0 (β1,15= -1.896; p = 0.0242). Similarly, the hazard of female patients moving from State II to State I was about 31% lower than for male patients (HR = 0.6879, CI = 0.5168-0.914) .
As body weight of patients show a unit change, the relative risk of patients to recover their CD4 cell count decreases by 99% to move through from State IV to State II (HR = 0.0067, CI = 0.0007-0.055). The estimate of the coefficient associated to the transition from State IV to State II is significantly different from 0 (β2,12= -5.0056; p= <0.0001). It means that a patient whose body weight was changed through follow-up time decreases the risk of leaving State IV to enter State II.
HIV infected patients with tuberculosis were 1.0682 times more likely to move from State I to State II than those of patients with no tuberculosis (HR = 1.0682, CI = 1.009-1.778). In back transition, HIV/AIDS patients with tuberculosis status positive were 0.08257 times less likely to move from State III to State II than those patients with no tuberculosis (HR = 0.08257, CI = 0.015- 0.445). Similarly, the risk of patients moving from State IV to State II for patients with tuberculosis were about 96% lower to move into State II than those of patients with no tuberculosis (HR = 0.03695, CI = 0.0076, 0.18). More precisely, the recovery rate of CD4 count from higher state to lower state for HIV/TB co-infected patients were small in relative to patients with no tuberculosis.
The estimated risk of HIV/AIDS infected patients with good adherence moving from State I to State II were about 10% lower than those of patients with poor adherence (HR = 0.9012, CI = 0.763-0.942). Similarly, the estimated risk of patients with good adherence moving from State I to death state were about 0.0535 times less likely to move into death state (State D) than those of patients with poor adherence (HR = 0.0535, CI = 0.0368-0.077). Conversely, patients with good adherence were 2.28 times more likely to move from State II to State I than those with poor adherence (HR =2.28, CI = 1.99-2.61). The risk of HIV/AIDS infected patients with good adherence moving from State II to State IV were about 73% lower than those of patients with poor adherence (HR = 0.272, CI = 0.1826-0.4025). It indicates that a patient with good adherence slows down the progression of the disease than those patients with poor adherence. Similar interpretation followed for back transition as, the risk of HIV/AIDS infected patients with Good adherence moving from State III to State I were about 2.38 times more likely to move into State I than those of patients with poor adherence (HR = 2.38, CI = 1.95-2.915). In line to this, patients with good adherence recover their CD4 count rapidly from State III to State I.
The result of the below Figure 1 indicates within the good states, the transition of patients from a given state (State I) to the next worst state increases with increasing time, reaches a maximum at a certain time, and then decreases with increasing time. It indicates that the risk of moving from State I to State II and from State I to State III was rapidly increasing the progression of AIDS disease among female patients than there male counterparts.
Figure 1. The Hazard Rate of Semi-Markov Process for the Transition of Sex of Patients = Male Coded as 0 (Black Line) and for Sex=Female Coded as 1 (Red Line)
The result of Table 4 log-likelihood for exponential and Weibull sojourn time distributions, indicates that a high Log-likelihood (6347.281) are observed when waiting time distribution is used in modeling HIV/AIDS disease progression, as compared with weibull waiting time distribution with Log-likelihood of 6064.183. Hence, the authors have preferred to choose the weibull sojourn time distribution as the stopping criterion was met after the second iteration.
Table 4. Log Likelihood and AIC of Exponential and Weibull Sojourn Time Distributions for HIV/AIDS Disease Progression
Moreover, exponential and Weibull sojourn time parametric distributions were fitted to each transitions of HIV/AIDS disease. The Akaike Information Criterion (AIC) for the models is shown in Table 4. As it can be seen, the Weibull distribution had a better fit than exponential sojourn time.
The findings showed that, most of the patients who moved to worst state were patients at the AIDS disease stage. The significant prognostic factors associated with transitions between stages of HIV/AIDS disease progression, includes age, ART adherence, TB status, functional status, opportunistic infection, sex, and body weight. The accelerating factors associated with higher risk of immune deterioration from good state to worst state was poor ART adherence, patient's co-infection with TB, older patients, being under opportunistic infections, and patients being bedridden. The conditional probabilities of HIV/AIDS patients from any good state to worst state are increasing over time. To predict lifetime of HIV/AIDS infected patients, the Weibull sojourn time distribution is appropriate and is preferably be used as sojourn time distribution under multistate semi- Markov model as compared to exponential sojourn time as it has lower AIC and Log likelihood and it is therefore, better for monitoring HIV/AIDS disease progression over time.