Proof of Beal's Conjecture and Fermat Last Theorem using Contra Positive Method
Vinay Kumar
Professor, Vivekananda School of IT, VIPS, GGSIPU, New Delhi, India.
Abstract
“If Ax + By = Cz , for integers A, B, C ≥2 and integers x, y, z greater than 2 , then A, B, C must have a common prime factor”. The statement is known as Beal's conjecture (Rubin & Silverberg, 1994). Without loss of generality, integers B and C can be expressed in terms of A. Assuming B = A + m and C = A + n, the present study proves the conjecture for all the four cases: i) m = 0, n = 0; ii) m = 0, n≠ 0; iii) m≠0, n = 0; and iv) m≠0, n ≠0. A, B, and C can be ordered (sequenced) in six different ways. A theorem that is proved for one sequence, the same theorem can easily be proved for other five sequences. Contrapositive approach together with integer division algorithm is used to prove the conjecture. Contrapositive statement of Beal's x conjecture is “if A, B, and C have no common prime factor then 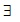 no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
Keywords :
- Beal's Conjecture,
- Fermat's Last Theorem,
- Fermat's General Proof,
- Division Algorithm,
- Exponent,
- Prime Factor,
- Contrapositive Proof
Introduction
Mathematicians have long been intrigued by Pierre Fermat's famous assertion that Ax + Bx = Cx has no positive integer solution for any integer x > 2. This assertion is known as Fermat's Last Theorem (FLT) (Aczel, 1996, pp. 123-134). The same assertion is mentioned in Kumar (2014) and Stewart and Tall (2002). Number theorists are divided while speculating whether or not Pierre Fermat actually had a proof. The mystery remains unanswered. However, the prevailing wisdom is that Fermat was mistaken as opined by Boston (1995) and Ribenboim (1999). While going through the works of Cornell et al. (1997), Granville and Monagan (1988), and Kumar (2012), it is observed that thousands of mathematicians have cumulatively spent millions of hours over the past 350 years searching unsuccessfully for such a proof. Although Wiles (1995) proved the FLT in 1994, yet many mathematicians believe that Fermat's proof could not possibly have been the proof discovered by Wiles as evident from Radford and Peirce (2006), and Stewart and Tall (2002). The proof provided by Andrew Wiles is not based on the mathematical concepts available when Fermat stated the theorem (Rubin & Silverberg, 1994). Researchers are of opinion that a number theoretic problems must be solved through number theoretic approach (Washington, 1997). Andrew Beal was working on FLT when he began to look at similar equations with independent exponents. He constructed several algorithms to generate solution sets, but the very nature of the algorithms he was able to construct required a common factor in the bases. He found that co-prime bases might be impossible and set out to test this hypothesis by computer. Andrew Beal and a colleague programmed 15 computers and after thousands of cumulative hours of operation had checked all variable values through 99. The solutions were found such that all had a common factor in the bases. Though the result was not conclusive, yet study provided sufficient reason to share his discovery with the world. He summarised his discovery as follows:
If Ax + By = Cz then A, B, and C must have a common prime factor, where A, B, C, x, y, and z are integers such that A, B, C ≥ 2 and x, y, z > 2 (Mauldin, 1997).
This is known as Beal's conjecture. Andrew Beal wrote many letters to mathematics periodicals and number theorists. Among the replies, two responses from number theorists were considered. Dr. Harold Edwards from the Department of Mathematics at New York University and author of “Fermat's Last Theorem, a generic introduction to algebraic number theory” confirmed that the discovery was unknown and called it “quite remarkable”. Dr. Earl Taft from the Department of Mathematics at Rutgers University relayed Andrew Beal's discovery to Jarell Tunnell who was “an expert on Fermat's Last Theorem”. Taft's response also confirmed that the discovery and conjecture were unknown. There is no known evidence of prior knowledge of Beal's conjecture and all references to it began after Andrew Beal's discovery in 1993 and subsequent dissemination of it (Mauldin, 1997). Expressing B and C in terms of A is used here to prove Beal's Conjecture and consequently FLT is proved using the Beal's conjecture.
Challenges
The Beal conjecture requires positive integers greater than or equal to 2 for bases A, B, C and strictly greater than 2 for exponents x, y, z in the case of equality. The products of the terms must reflect the selfsame multiplication of the terms in whole numbers or positive integers. Obviously, no fractional expressions are to appear in any of the three terms or three exponents of the equation. The most significant part in the proof of the conjecture requires that the terms: A, B, and C share a common prime divisor, if there is a solution to the equation. Finding a relationship among A, B, and C is a challenge because of arbitrariness of values that exists for A, B, and C. Any algorithm to find base triplet (A, B, C) for a exponent triplet (x, y, z) may produce an example, but not a proof of the conjecture. B and C are expressed in terms of A to prove Beal's Conjecture and consequently proof for FLT.
Motivation
Beal's conjecture was widely received with enthusiasm by the mathematics community. The motivating factor for attempting this proof has been a way through which FLT can be proved using number theoretic approach as described by Ireland and Rosen (1990), Jacobson (1989), and Kumar (2015). The success of the approach used among base triplet (A, B, C) motivated to complete this proof. Second factor has been an accidental visit to the University of North Texas website http://www.math.unt.edu/~mauldin/beal.html, which contains information regarding $1,000,000 cash prize that is held in trust by the American Mathematics Society.
Application of number theory in Information security, Privacy, Cryptography, and Steganography, has been another motivation to attempt this open problem. In this paper, multiplication sign is not used explicitly. Two variables (subscripted or un-subscripted) appearing together in a mathematical expression represent their product, i.e., xy stands for x*y. The other arithmetic operators are used explicitly wherever required.
1. Formulation of Problem
Let
be true under given constraints. Without loss of any generality, we can write equation (1) as,
where, m and n are positive integers. Integers A, B, and C can have any of the possible six order relationships: A ≤ B ≤ C; A ≤ C ≤ B; B ≤ A ≤ C; B ≤ C ≤ A; C ≤ A ≤ B; and C ≤ B ≤ A. In any of the six cases, we can write equation (1) as equation (2) by just replacing A with B or C as the case may be. Let us take case one, other can be proved similarly. From equation (2), we have,
There are following four possibilities for m and n:
Case 1: When m = 0 and n = 0
In this case, the result is obvious because Right Hand Side (RHS) of equation (3) is zero and A, B, and C have integer A in common. If A is prime, then there exists a prime factor A in A, B, and C. If A is a composite number then a prime factor in A is prime factor in A, B, and C.
Case 2: When m = 0 and n≠0
In such cases, nz in the RHS of equation (3) must be a multiple of A because Left Hand Side (LHS) of equation (3) is divisible by A and all other terms in RHS of the equation are divisible by A. This is possible only if there is a prime factor p between A and n, such that for z some , n z is divisible by A. Since p is a prime factor in A and n, p is also a prime factor in B (= A + m) and C (= A + n).
Case 3: When m ≠ 0 and n = 0
The case is similar to case 2 and it needs no additional detailing.
Case 4: When m ≠ 0 and n ≠ 0
Since x, y, and z are greater than 2, LHS of equation (3) is divisible by at least A, A2 , and A3 and therefore RHS must also be divisible by A, A2 , and A3 . We have to prove that there exists a prime factor p such that p is common in A, B, and C, i.e. p is common in A, A + m, and A + n, i.e. p is common in A, m, and n. Contrapositively, if there is no prime common factor in A, m and n, then equation (2) is not valid under the given constraints.
2. Construction of Proof of the Conjecture
If RHS of equation (3) is divisible by A then (nz– my ) must be divisible by A because all other factors in RHS are divisible by A. If RHS is divisible by A then there exists an integer k1 such that
Similarly, if RHS of equation (3) is divisible by A2 then the component of equation (3), (znz-1 -ymy-1)A+(nz – my ) must be divisible by A2 . And thus there exists an integer k2 such that
and, if RHS of equation (3) is divisible by A3 , then there exists an integer k3 such that
We now proceed to prove that if there is no common prime factor in A, B, and C, i.e., in A, A + m, and A + n, i.e., in A, m, and n, then there exists no integers k1 , k2 , k3 such that equations (4) through (6) are satisfied.
Let p be a common prime factor in A, m, and n such that A = k4p, m = k5p, and n = k6 p, where k4 , k5 , and k6 are positive integers because A, m, and n are positive integers. Now, in order to prove the theorem, we have to prove that if equations (4), (5), and (6) are satisfied then p exists. Contrapositively, if there is no common prime factor p in A, A + m, and A + n, then equations (4), (5), and (6) are not true. In other way if p does not exist, then there exists no integers k1 , k2 , k3 such that equations (4), (5), and (6) are satisfied.
Replacing A, m, and n, respectively with k4p , k5p, and k6p in equations (4), (5), and (6), we have the following equations: From equation (4), we get
From equation (5), we have
And from equation (6), we have
Now multiplying equation (7) by z, multiplying equation (8) by k6 and then subtracting equation (7) from equation (8), we get
Multiplying equation (9) by k62p and equation (7) by z(z – 1) k6 and then subtracting equation (7) from equation (9), we get
Now, multiplying equation (10) by [z (z – 1) k52 – y (y – 1)k62 ], multiplying equation (11) by k5 [k5 z – k6 y] and then equating these two equations, we get
Applying the additive cancellation for the term [k52 z2 (z – 1) k1 k4 ] in the above equation we get,
Since y and z are positive integers greater than 2, z(z – 1) and y(y – 1) are positive even integers. On replacing z(z – 1) and y(y – 1) with 2a and 2b, respectively in the above equation, we get
Equation (12) is a quadratic equation in prime p. If p is a prime number then roots of equation (12) must be prime number. We derive the proof of the conjecture in the following section.
3. Final Proof of the Conjecture
It is obvious that all coefficients in equation (12) are integers. Let
Integers D, E, and F are results of arithmetic expressions in y, z, k4 , k5 , and k6 and therefore D, E, and F are integers. Existence of y, z, k4 , k5 , and k6 depend on the existence of p. Then equation (12) can be rewritten in simplified form as equation (13) below.
Equation (13) is a quadratic equation for prime number p with integer coefficient. A quadratic equation uq2+vq+w = 0 with integer coefficients u, v, and w has both roots integers if and only if
- v2 – 4uw is a perfect square or zero, and
- leading coefficient u divides v and w.
The proof of the above statement is available in (Zelator, 2011).
It is possible, in some cases, that the leading coefficient u does not divide v and w. In such case, the two roots of the equations will be rational roots. For one of the rational roots to be a prime integer (or a positive integer greater than 1 because a positive integer greater than 1 can be written as product of distinct primes), coefficient v must be of the form – (α + up). This is proved in the following lemma.
Lemma:
A quadratic equation uq2 +vq+w=0 with integer coefficients u, v, and w has one rational and one integer root greater than 1, then v must be of the form –(α + up) and w = αp, where α/u is rational root and p > 1 is a positive integer root. Here α is an integer and u is a positive integer, which is also a leading coefficient in the equation.
Proof:
Let the two rational roots be α/u and p, where α/u is rational number and p is a positive integer root greater than 1. Then the equation can be written as,
Therefore, equation (13) has a solution in p if and only if 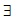 k1 , k2 , and k3 such that either k3D divides k2E, k1F, and the discriminant is a perfect square, or k2E = α +k3Dp and k1F =αp, i.e., if common factor p does not exists then k1 , k2 , k3 do not exist ♦
k1 , k2 , and k3 such that either k3D divides k2E, k1F, and the discriminant is a perfect square, or k2E = α +k3Dp and k1F =αp, i.e., if common factor p does not exists then k1 , k2 , k3 do not exist ♦
For Example, the solution 33 +63 = 35 has bases with a common prime factor of 3. It is an example of case 3 when m ≠0 and n= 0. The solution 73 +74 = 143 has bases with a common prime factor of 7. It is an example of case 2 when m = 0 and n≠ 0 and 2n+2n =2n+1 has bases with a common prime factor of 2. It is an example of case 1 when m = 0 and n = 0. In fact the equation has infinitely many solutions where the bases share a common factor.
Let us consider an example of case 4 when m≠0 and n ≠ 0. In equation A5 + B3 = C4 , we have A = 8, B = 32, and C = 16. In this case, the coefficients of quadratic equation (13) are u = 172800, v = 559104, and w = –1809408. Equation (13) in this case is
172800 p2 + 559104 p – 1809408 = 0
or 172800 p2 – (– 904704 + 2 * 172800)p + (– 904704)*2 = 0
where α = – 904704, u = 172800. The integer root is p = 2 and other rational root is –904704/172800¨♦
It means if A, B, and C has no common integer factor p, then equations (4) through (6) are not satisfied. Therefore, if there is no common prime factor p, then equation (3) is not satisfied and thereof equation (1) is not true. Using the contrapositive statement, it can be concluded that if equation (1) is true then there is a common prime factor in A, B, and C.
4. Proof of FLT
Fermat's famous assertion that “Ax + Bx = Cx has no positive integer solution for x > 2” is known as Fermat's Last Theorem. The theorem is proved by method of contradiction.
Let Ax + Bx = Cx has a positive integer solution for any x > 2. Then by Beal's conjecture, A, B, and C have a common prime factor. Let the largest common factor be p. If p is not prime number then p can be written as product of primes. Since p is a factor in A, B, and C, we can write
A = pA1 , B = pB1 , C = pC1
for some positive integers A1 , B1 , C1 , and there is nothing common in A1 , B1 , C1 . After cancelling out the common factor p, the equation,
reduces to
for x > 2. It is also true that in this reduced equation, none of A1 , B1 , C1 is equal to 1 because there exist no positive integers D, E for x > 2 such that
Dx +1x = Ex
Since there is no common factor in A1 , B1 , C1, validity of equation (15) is in contradiction with Beal's conjecture. Thus Ax + Bx = Cx has no positive integer solution for x > 2.
Conclusion
There can be no problem in the field of physics, chemistry, or biology that has so vehemently resisted attack for so many years as the Fermat's Last Theorem, finding closed form formulae for Fibonacci recursive equation and recently this Beal's conjecture. It was predicted that civilization would come to an end as a result of Nuclear war before Fermat's Last Theorem would ever be resolved (Kumar, 2010). In 1994, Andrew Wiles of Princeton University announced a proof while working on a more general problem in geometry. Andrew Wiles came out with a proof that is very lengthy and cumbersome. It is even doubted as a mathematical proof of the theorem (Mauldin, 1997). A number theory problem must be solved through number theoretic approach. The author of this paper published a proof of FLT (Kumar, 2014), based on number theoretic approach and the knowledge gained in the process has helped in formulating this proof. Formulation of problem for four possible cases of m and n has helped in proving the Beal's conjecture and subsequently proving the FLT.
There is no royal road to logic. Nature is innately mathematical and she speaks to us in mathematical language. We only have to listen to describe nature in mathematical form (Silverman, 1986). The approach to express B and C in terms of A has simplified the entire process. A close attention always provides some valuable ideas, which are always simple when brought before the world in simple way.
Acknowledgment
Existence of a problem inspires one to think for its solution. A complicated problem is generally solved by working around basic concept. “How unlearning (or keeping aside higher knowledge for sometimes) helps in solving some longstanding problem” is an important lesson learnt here. One has to look around to know the presence of something worth noticing. Special thanks to some reviewers of this work for giving some helpful suggestions. I am grateful to those reviewers also who made very harsh comments in words.
References
[1]. Aczel, A. D. (1996). Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem. N. Y.:Dell Publishing.
[2]. Boston, N. (1995). A Taylor-made plug for Wiles' proof. The College Mathematics Journal, 26(2), 100-105.
[3]. Cornell, G., Silverman, J., and Stevens, G., (eds.) (1997). Modular Forms and Fermat's Last Theorem. Springer- Verlag.
[4]. Granville, A., & Monagan, M. B. (1988). The first case of Fermat's last theorem is true for all prime exponents up to 714,591,416,091,389. Transactions of the American Mathematical Society, 306(1), 329-359.
[5]. Ireland, K., & Rosen, M. (1990). A Classical Introduction to Modern Number Theory (Vol. 84). Springer Science & Business Media.
[6]. Jacobson, N. (1989). Basic Algebra II, 2ndEd. New York: W. H. Freeman.
[7]. Kumar, V. (2010). Restricted backtracked algorithm for Hamiltonian circuit in undirected graph. BIJIT-BVICAM's International Journal of Information Technology, 2(2), 23-32.
[8]. Kumar, V. (2012). Mathematics Is Science: A topic revisited in context of FCS of India. International Journal of Modern Education and Computer Science, 4(6), 17-26.
[9]. Kumar, V. (2014). Proof of Fermat last theorem based on odd even classification of integers. Int. J. Open Problems Compt. Math., 7(4), 23-34.
[10]. Kumar, V., (2015). Discrete Mathematics. New Delhi: BPB Publication.
[11]. Mauldin, R. D. (1997). A generalization of Fermat's Last Theorem: The Beal conjecture and prize problem. Notices of the American Mathematical Society, 44(11), 1436-1437.
[12]. Radford, L., & Peirce, C. S. (2006, November). Algebraic thinking and the generalization of patterns: A semiotic perspective. In Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics
Education, North American Chapter (Vol. 1, pp. 2-21).
[13]. Ribenboim, P. (1999). Fermat's Last Theorem for Amateurs. New York: Springer-Verlag.
[14]. Rubin, K., & Silverberg, A. (1994). A report on Wiles' Cambridge lectures. Bulletin of the American Mathematical Society, 31(1), 15-38.
[15]. Silverman, J. H. (1986). Heights and elliptic curves. In Arithmetic Geometry (pp. 253-265). Springer, New York, NY.
[16]. Stewart, I., & Tall, D. (2002). Algebraic Number Theory and Fermat's Last Theorem, 3rd Ed. AK Peters/CRC Press.
[17]. Washington, L. C. (1997). Introduction to Cyclotomic Fields (Vol. 83). Springer Science & Business Media.
[18]. Wiles, A. (1995). Modular elliptic curves and Fermat's last theorem. Annals of Mathematics, 141(3), 443-551.
[19]. Zelator, K. (2011). Integer Roots of Quadratic and Cubic Polynomials with Integer Coefficients. arXiv preprint arXiv:1110.6110.
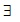 no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.
no integers A, B, C and integers x, y, z > 2 such that Ax + By = Cz”. Some basic and fundamental properties of quadratic equation are also used in the proof.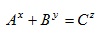
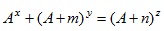
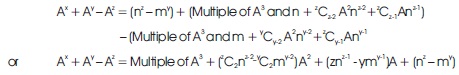
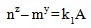
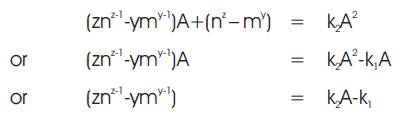
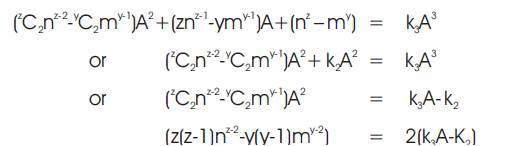
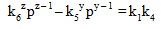

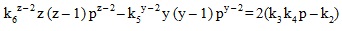
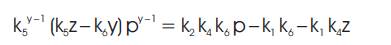
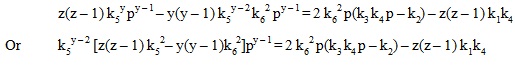
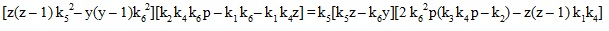
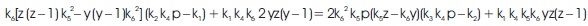

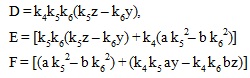
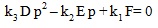
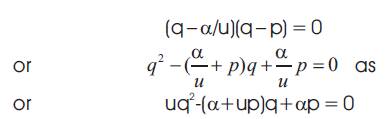
 k1 , k2 , and k3 such that either k3D divides k2E, k1F, and the discriminant is a perfect square, or k2E = α +k3Dp and k1F =αp, i.e., if common factor p does not exists then k1 , k2 , k3 do not exist ♦
k1 , k2 , and k3 such that either k3D divides k2E, k1F, and the discriminant is a perfect square, or k2E = α +k3Dp and k1F =αp, i.e., if common factor p does not exists then k1 , k2 , k3 do not exist ♦