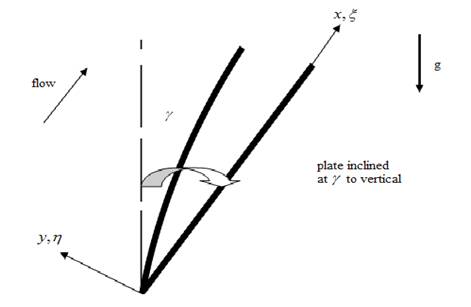
Figure 1. Physical Model and Coordinate System
The present paper investigates the radiation effect on the boundary layer flow of an incompressible non Newtonian Jeffrey fluid from an inclined vertical plate. Mathematical Formulation of the problem is achieved by appropriate nonsimilarity transformations. The transformed non-dimensional, coupled, and highly non-linear system of equations is solved numerically using the efficient Keller-box implicit finite difference method. Physical features of the involved parameters are presented and discussed through the graphs. The influence of many multi-physical parameters of these variables are illustrated graphically. The results found that, increasing the radiation parameter (R) on velocity and temperature profiles, increases the skin friction coefficient, but heat transfer coefficient decelerates.
Many modern engineering applications involve the study of non-Newtonian fluids. Analysis of non-Newtonian fluids have been the effort of several investigations during the past few decades because of its extensive engineering and industrial applications. Especially, flow and heat transfer of non-Newtonian fluids play an important role in food engineering, petroleum production, power engineering, in polymer solutions and in polymer melt in the plastic processing industries. The constitutive Jeffery fluid model is explained is [1, 4, 6, 7, 18, 23] and they have included several different physical effects. These flows appear in a wide variety of engineering applications, as well as in many natural conditions such as geothermal extraction, storage of nuclear waste material, oil recovery procedures, ground water flows, etc. Thus researchers are attracted to investigate its thermo physical properties.
The heat transfer from inclined surfaces finds numerous applications in solar energy systems, geophysics, materials processing, etc. Many studies have appeared concerning natural and also mixed convection flows. Kierkus [10] studied isothermal inclined plate natural convection boundary layer flow using a perturbation method for a Prandtl number of 0.7. Fujii and Imura [5] studied experimentally free convection from an inclined plate. Uniform surface flux effects on inclined plate thermal convection were reported by Armaly, et al. [2]. Wickern [24] examined the laminar boundary layer flow over an arbitrarily sloping plate showing that for opposing buoyancy forces singular as well as regular behaviour may prevail. Nagendra et al. [11] Investigated numerical analysis of non-Newtonian Fluid from a sphere with the presence of Nano particles. Satyanarayana and Harish [3] discussed Numerical study of MHD heat and mass transfer of a Jeffrey fluid over a stretching sheet with chemical reaction and thermal radiation. Hayat et al. [8] studied Soret and Dufour effects on MHD Peristaltic Flow of Jeffrey Fluid in a Rotating System with Porous Medium. Subba Rao, et al. [18] investigated Thermal Radiation Effects on Oldroyd-B Nano Fluid from a Stretching Sheet in a Non- Darcy Porous Medium and he has used the Keller Box method. Subba Reddy, et al. [20] explained Slip effects on the peristaltic motion of a Jeffrey fluid through a porous medium in an asymmetric channel under the effect magnetic field. Nagendra, et al. [12] deliberated Peristaltic flow of a Jeffrey fluid in a tube. Raju et al. [14-16] demonstrated the combined effects of radiation and chemical reaction on vertical plate by using analytical methods. Reddy et al. [21, 22] studied the unsteady boundary layer flow past a moving plate/channel.
The objective of the present study is to examine 'Radiation effect on the boundary layer flow of a non- Newtonian Jeffrey fluid from an inclined vertical plate. The effects of governing thermo physical parameters on heat transfer characteristics are analyzed in detail. Mathematical modelling through equations of continuity and motion leads to dimensionless nonlinear coupled differential boundary layer equations. Numerical solutions for the velocity and the temperature distributions are obtained using a Keller-Box finite difference method.
The steady, two-dimensional, incompressible boundary layer flow, heat transfer of a Jeffrey's fluid from an inclined vertical plate is considered. Jeffery rheological fluid is examined, as illustrated in Figure 1. Both the plate and the Jeffrey's fluid are maintained at a constant temperature. Instantaneously they are raised to a temperature T > T , the ambient temperature w of the fluid which remains unchanged. The x- coordinate (tangential) is measured from the leading edge of the plate and ycoordinate (radial) is measured normal to the plate.
Figure 1. Physical Model and Coordinate System
The corresponding velocities in the x and y directions are u and v, respectively. The governing conservation equations can be written as follows:
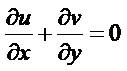
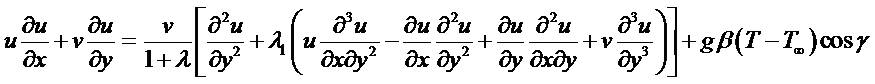
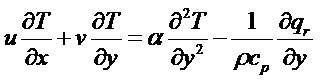
The boundary conditions are prescribed at the surface and the edge of the boundary layer regime, respectively as follows:
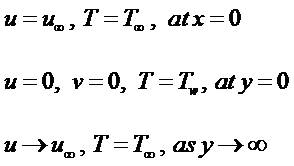
The stream function is defined by and , and therefore, the continuity equation is automatically satisfied. In order to write the governing equations and the boundary conditions in dimensionless form, the following non-dimensional quantities are introduced.
where u and v are the velocity components in the x and y- directions, respectively, the kinematic viscosity of the conducting fluid, - is the coefficient of thermal expansion, - the thermal diffusivity, k - the thermal conductivity, - inclination of the plate to the vertical, - is the density of the fluid, C - the specific heat at constant pressure, - the ratio of p relaxation to retardation times, - the retardation time, Pr - Prandtl number, Gr - Grashof number, De - Deborah number, T - 1 * the free stream temperature, R- the radiation parameter, k - the Roseland mean absorption coefficient, * - the Stefan- Boltzmann constant, the thermal buoyancy force parameter which is a measure of thermal buoyancy force effect on forced convection, - Local Reynolds number respectively.
We assume that the temperature differences within the flow are sufficiently small such that T may be expressed as a linear 4 function of temperature, we can expand T in Taylor's series about T and neglecting the higher order terms beyond the first 4 3 4 degree (T - T ), we get T ≅ 4T T-3T
In view of equation (5), equations (2) - (3) reduce to the following coupled, nonlinear, dimensionless partial differential equations for momentum and energy for the regime:
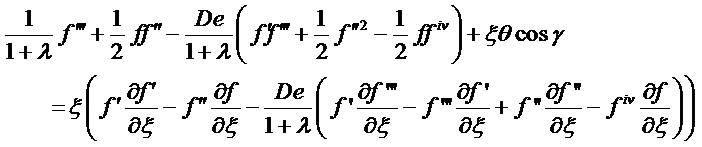
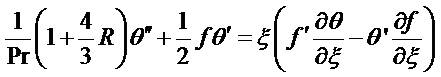
The dimensionless form of the boundary conditions are,
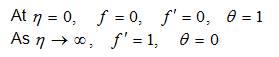
The engineering design quantities of physical interest include the skin-friction coefficient and Nusselt number, which are given by:
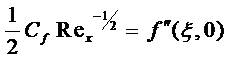
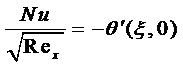
In this study, the efficient Keller-Box implicit difference method has been employed to solve the general flow model defined by equations (6) – (7) with boundary conditions in equation (8). This method was originally developed for low speed aerodynamic boundary layers and this system is developed by Keller [9] and this technique has been described briefly in Cebeci and Bradshaw [3]. This method has been employed in a diverse range of industrial multi-physical fluid dynamics problems. These include Casson slip boundary layer flows [17, 19]. This method remains among the most powerful, versatile and accurate computational finite difference schemes employed in modern viscous fluid dynamics simulations. This method has been used extensively and effectively for over three decades in a large spectrum of nonlinear fluid mechanics problems. Keller's method provides unconditional stability and rapid convergence for strongly non-linear flows. It involves four key stages, summarized below.
Comprehensive solutions have been obtained and are presented in Figures 2 to 5. The numerical problem comprises two independent variables ( , ), two dependent fluid dynamic variables (f, ), and 6 thermo-physical and body force control parameters, namely Pr, , De, R, , and . The following default parameter values, i.e. Pr = 0.71, = 0.2, De = 0.1, R = 0.5, = 0 1.0, = 70 are prescribed.
Figures 2(a) and 2(b), represent the evolution in the effect of the ratio of relaxation to retardation times, i.e. on the velocity (f') and temperature ( ). Fluid flow is significantly increases with increasing . Conversely, temperature is depressed slightly with increasing values of through the boundary layer.
Figure 2. (a) Influence of l on Velocity Profiles, (b) Influence of l on Temperature Profiles
Figures 3(a) and 3(b) illustrate the velocity (f') and temperature ( ) with a difference in Deborah number (De). The velocity component of the fluid flow (Figure 3(a)), a temperature component of the fluid (Figure 3(b)) is considerably reduced with increasing De through the surface of the plate.
Figure 3. (a) Influence of De on Velocity Profiles, (b). Influence of De on Temperature Profiles i-
Figures 4(a) and 4(b) explain the influence of the radiation parameter on the dimensionless velocity and temperature. Increasing radiation parameter R, the velocity slightly increases throughout the boundary layer. Further, temperatures are more enhanced.
Figure 4. (a). Influence of R on Velocity Profiles, (b) Influence of R on Temperature Profiles
Figures 5(a) and 5(b) show the effect of radiation parameter R, on inclined plate surface shear stress (f'') and local Nusselt number (- ') variation. In consistency with the earlier graphs described for velocity evolution, with an increase in R, wall shear stress is consistently condensed, i.e. the flow is accelerated along the inclined plate surface. Increasing R, is found to decrease the local Nusselt number throughout the boundary layer.
Figure 5. (a) Influence of R on Skin Friction Coefficient Results, (b) Influence of R on Nusselt Number Results
The work motivated by applications in non-Newtonian fluid model has been developed for Radiation effect on the boundary layer flow of a Jeffery's fluid from an inclined vertical plate. The governing equations are solved numerically by the finite difference method. Numerical results are reported for various values of selected parameters interest.
C - Skin Friction Coefficient
f - Non-dimensional Steam Function
g - Acceleration due to Gravity
k - Thermal Conductivity of Fluid
c - Specific Heat Parameter
Gr - Grashof Number
Nu - Nusselt Number
Pr - Prandtl Number
De - Deborah Number
R - Radiation Parameter
T - Temperature of the Fluid
u, v - Non-dimensional Velocity Components along the x- and y- Directions, respectively
x - Stream-wise Coordinate
y - Transverse Coordinate
a- Thermal Diffusivity
b- The Coefficient of Thermal Expansion
l- Ratio of Relaxation to Retardation Times
l- Retardation Time
h- Dimensionless Radial Coordinate
m- Dynamic Viscosity
n- Kinematic Viscosity
q- Non-dimensional Temperature
r- Density
x- Dimensionless Tangential Coordinate
y- Dimensionless Stream Function
w - Conditions at the wall surface
¥- Free stream conditions