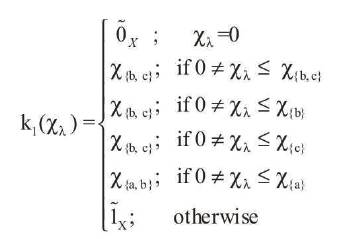
In the present paper, the authors have aimed to introduce fuzzy connectedness in fuzzy biclosure space. Here they generalize the concept of fuzzy connectedness in fuzzy closure space to fuzzy biclosure space. They also investigate the fundamental properties of fuzzy connectedness in fuzzy biclosure space.
Čech Closure space was introduced by E. Čech [ 3] in 1966. Fuzzy Čech Closure space was first introduced by the A.S. Mashhour and M.H. Ghanim [ 6]. The notions of closure system and closure operator are very useful tools in several areas of classical mathematics. They play an important role in topological spaces, Boolean algebra, convex sets, etc.
Biclosure space was introduced by Chandrasekhar Rao, Gowri, and Swaminathan [ 8]. Fuzzy biclosure space was introduced by Tapi U.D. and Navalakhe R. [ 11]. Such spaces are equipped with two arbitrary fuzzy closure operators. He extended some of the standard results of separation axioms in fuzzy closure space to fuzzy biclosure space. Thereafter a large number of papers have been written to generalize the concept of fuzzy closure space to fuzzy biclosure space. In this paper, the authors have introduce fuzzy connectedness in fuzzy biclosure space and studied some of its fundamental properties.
An operator u : P(x) →P(x) defined on the power set P(X) of a set X satisfying the axioms:
is called a Čech closure operator and the pair (X, u) is a Čech closure space.
Two maps u1 and u2 from power set of X to itself are called biclosure operators for X if they satisfy the following properties:
A structure (X, u1, u2) is called a biclosure space
A closure space (X, u) is connected if there exists any continuous mapping f from X to the discrete space {0, 1} is constant. A subset A in a closure space (X, u) is said to be connected if A with the subspace topology is a connected space.
Let (X, u1, u2) and (Y, v1, v2) be biclosure spaces and let i ∈{1,2}. Then a mapping f: (X, u1, u2) →(Y, v1, v2) is called
(i) i -open (respectively, i -closed) if the mapping f: (X, ui) →(Y, vi) is open (respectively, closed).
(ii) Open (respectively, closed) if f is i-open (respectively, i-closed) for all i ∈{1,2}.
(iii) i -continuous if the mapping f: (X, ui) →(Y, vi) is continuous.
(iv) Continuous if f is i-continuous for all i∈ {1,2}.
Let X is a non empty fuzzy set. A function k: Ix→ Ix is called fuzzy Čech closure operator on X if it satisfies the following conditions
The pair (X, k) is called fuzzy Čech closure space.
Let (X, u) and (Y, v) be fuzzy closure spaces. A mapping f: (X, u)→ (Y, v) is said to be fuzzy continuous if f(u(χ{λ}))≤v{f(χ{λ})}for every fuzzy subset λ≤Ix
Let X is a nonempty fuzzy set. A mapping k: Ix→ Ix is called fuzzy Čech closure operator on X. A fuzzy Čech closure space (X, k) is said to be fuzzy connected if and only if any F-continuous mapping f from X to the fuzzy discrete space {0, 1} is constant.
Let (x, u1, u2) and (Y, v1, v2) be fuzzy biclosure spaces and let i∈ {1, 2}. A map f: (X, u1, u2) (Y, v1, v2) is called fuzzy i- continuous if the mapping f: (X, ui) (Y, vi) is fuzzy continuous. A mapping f is called fuzzy continuous if f is fuzzy i- continuous for each i∈{1, 2}.
Let X is a nonempty fuzzy set and ki : Ix→ Ix for i = {1, 2} is called fuzzy closure operators on X. A fuzzy biclosure space i (x, k1, k2) is called fuzzy connected if and only if any F-continuous mapping f from X to the fuzzy discrete space {0, 1} is constant.
Let X= {a, b, c} is a non empty set. Define fuzzy closure operator k1 : Ix→Ix such that,
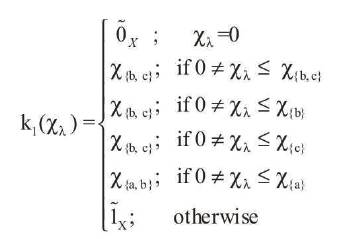
Hence (X, k1 ) is a fuzzy closure space
FOS (X, k2)
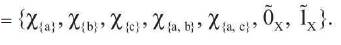
For another fuzzy closure operator k2 : Ix→ Ix such that,
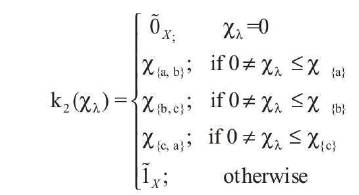
Hence (X, k2) is a fuzzy closure space.
FOS (X, k2)
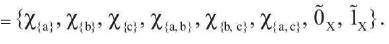
So here (X, k1 , k2 ) is a fuzzy biclosure space.
Fuzzy open sets of fuzzy biclosure space (X, k1, k2 )
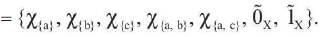
We define an F-continuous mapping f:X→{0,1} such that
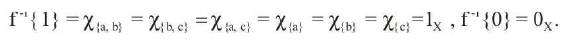
Here mapping f is constant. Hence (X, k1 , k2 ) is a fuzzy connected fuzzy biclosure space.
Let X = {a, b, c, d} is a non empty set and consider a fuzzy closure operator which is defined by k2 : Ix→Ix such that,
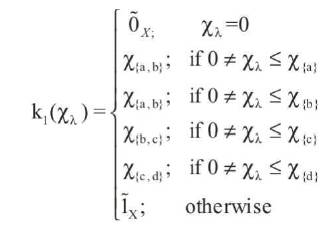
For all fuzzy subsets λ≤Ix let
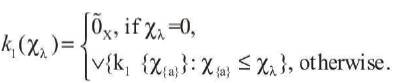
Hence (X, k1) is a fuzzy closure space.
Fuzzy open sets of(X,k1)
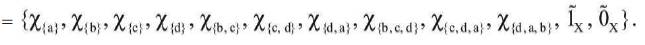
Consider another fuzzy closure operator k2 : Ix→Ix such that
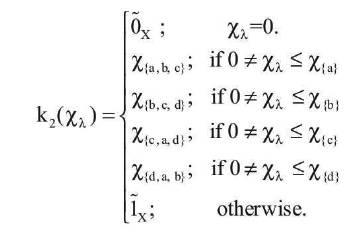
For all fuzzy subsets χλ≤Ix let,
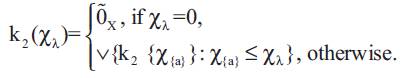
Hence (X, k2 ) is a fuzzy closure space.
Fuzzy open sets of fuzzy closure space,
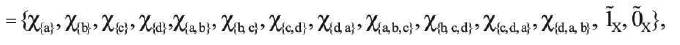
Here (x, k1 , k2 ) is a fuzzy biclosure space.
Fuzzy open sets of fuzzy biclosure space (x, k1 , k2 ) are,
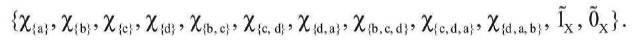
Let f:X→{0,1} is a F-continuous mapping such that,
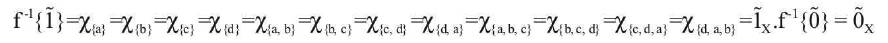
Here F-continuous mapping f is constant.
Hence (X, k1 , k2 ) is a fuzzy connected fuzzy biclosure space.
A fuzzy biclosure space (X, k1 , k2 ) is fuzzy connected if and only if it has no separation.
If (X, k1 , k2 ) is fuzzy connected fuzzy biclosure space and it has a separation . Define f:X→{0,1} by
. Define f:X→{0,1} by 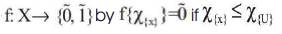
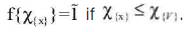 ifχ{x}≤χ{y} . Then F-mapping f is continuous but not constant. It contradicts the fuzzy connectedness of fuzzy
biclosure space (X, k1 , k2 ).
ifχ{x}≤χ{y} . Then F-mapping f is continuous but not constant. It contradicts the fuzzy connectedness of fuzzy
biclosure space (X, k1 , k2 ).
Hence fuzzy biclosure space (X, k1 , k2) has no separation.
Conversely, consider fuzzy biclosure space (X, k1 , k2 ) has no separation, if X is not fuzzy connected. Then there exists an F-continuous map f:X→{0,1} is not constant.f-1(0) and f-1(1) is non-empty and 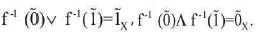 ,
,
Thus fuzzy biclosure space X has a separation f-1(0),f-1(1). Hence fuzzy biclosure space (X, k1 , k2 ) is fuzzy connected.
An F-continuous image of a fuzzy connected fuzzy biclosure space is fuzzy connected.
Let f : X→ Y be an F-continuous surjective map where X, Y are fuzzy biclosure spaces and X is fuzzy connected fuzzy biclosure
space. Suppose fuzzy biclosure space Y is not fuzzy connected, and then by definition, F-continuous function f is not
constant. Y has a separation, say χu|χv . Let 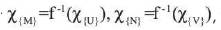 , then
, then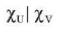 are disjoint fuzzy open sets of X. This
contradicts the fact that X is fuzzy connected fuzzy biclosure space. Therefore Y must be fuzzy connected fuzzy biclosure
space.
are disjoint fuzzy open sets of X. This
contradicts the fact that X is fuzzy connected fuzzy biclosure space. Therefore Y must be fuzzy connected fuzzy biclosure
space.
The union of any family of fuzzy connected sets of fuzzy biclosure space (X, k1 , k2 ) with a common point is fuzzy connected.
Let χ{xa} be a family of fuzzy connected sets and 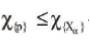 for all α. Let
for all α. Let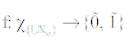 be any fuzzy continuous map and
be any fuzzy continuous map and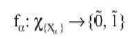 be the restriction of f to
be the restriction of f to 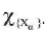 . Since f is F-continuous, each fα is F-continuous and Xα is fuzzy connected so fα is
constant. Now let
. Since f is F-continuous, each fα is F-continuous and Xα is fuzzy connected so fα is
constant. Now let 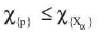 for all α and
for all α and  for all α and
for all α and 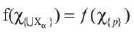 , i.e. f is constant. Thereforeχ{UXα}
is fuzzy connected set of fuzzy biclosure space (X, k1 , k2 ).
, i.e. f is constant. Thereforeχ{UXα}
is fuzzy connected set of fuzzy biclosure space (X, k1 , k2 ).
Let χ{λ1}and χ{λ2}are fuzzy subsets of a fuzzy connected fuzzy biclosure space (X, k1 , k2 ) such that,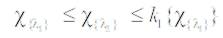 and
and  is fuzzy connected, and then χ{λ2}is fuzzy connected.
is fuzzy connected, and then χ{λ2}is fuzzy connected.
For each point χ{p} in a fuzzy connected fuzzy biclosure space (X, k1 , k2 ) the component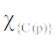 . of X is the largest fuzzy 1 2
connected set in X which contains the point χ{p}.
. of X is the largest fuzzy 1 2
connected set in X which contains the point χ{p}.
For each point χ{p} in a fuzzy connected biclosure space (X, k1 , k2 ), the component χ{C(p)} is a fuzzy closed set.
In this paper, the idea of fuzzy connectedness in fuzzy biclosure space was introduced. Fuzzy connectedness is very useful in image segmentation. In image segmentation, fuzzy connectedness is used in fuzzy topological space. Fuzzy closure space is the generalization of fuzzy topological space. Fuzzy connectedness in fuzzy closure space gives strength of connectedness between every two pairs of image pixels is considered. Fuzzy connectedness is also useful in digital image processing which is helpful in medical sciences.