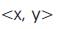 satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012) .
satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012) .This monograph provides an epistemological rational for a novel science grounded in trichotomous statistical analysis metrics. Triology is the study of the trifold nature of phenomena. It has its foundation in the mathematical “Law of Trichotomy”. Triology is measured using the Tri–Squared Statistic. Advanced post hoc measurement of Triology is conducted using Triostatistics (or more simply “Triostat”) is the application of Post Hoc measures to the statistically significant outcomes of the Trichotomous Squared Test. Triology involves a variety of concepts that are defined using robust and rigorous calculations provided in this paper. It uses its computations to provide further insight on the inner workings of the threefold aspects of nature. The topology and taxonomy of the triology are covered in detail along with Tri–Squared and Triostatistics procedures.
In the study of the intricate and complex components of nature, one will begin to notice the “trifold” or “threefold” nature of life. The specific study of life's trifold nature is the science of “Triology”. Triology is defined as the science concerned with the discovery, study, and analysis of the triadic, tripartite, and triplex elements, components, and cycles of thought, learning, life, and nature through triplicate structural, hierarchical, and sequential levels of topology, taxonomy, and theology.
A topology is collectively and formally defined as “the study of qualitative properties of certain objects”. The qualitative properties of the objects concerned with the internal and external dynamics of the science of three are formally defined in three holistic terms. The three major terms of the science of triology that place specific emphasis on the trifold nature of science and the practice of trichotomous scientific inquiry in terms of “three” are:
Each of these terms is individually defined as follows:
By definition, the term “Trichotomy”: is pronounced ['trahy-kot-uh-mee'], spelled “tri.choto.my”, and is a noun with the plural written form “tri.chot.o.mies”. “Trichotomy” has the following threefold definition:
For example – “A trichotomy between thought, emotions, and action” (Osler, 2012). “Taxonomy” is broadly defined as the practice and science of classification of things or concepts, including the principles that underlie such classification. Thus, a scientific systemic classification methodology is the more general definition of the term “Taxonomy”. The term taxonomy is and of itself is a portmanteau that was originally derived from the combination of the two Greek terms “taxis” (that literally means “the arrangement of” or “the division of”) and “nomos” (which is the Geek word for “law”). In practice, a taxonomy classifies some predetermined system, creating a framework (sometimes conceptual) providing an in–depth structure for further discussion, critique, critical analysis, and/or definition. The particular elements of a given taxonomy are referred to as individual “taxons” and can be arranged into smaller subgroups referred to as “taxa”. In terms of the science of triology, its taxonomy is a primary schema grounded in the “Mathematical Law of Trichotomy”. Its operational methodology is the division of a given natural phenomenon or a universal concept into a mutually exclusive set (or group) of interdependent and independently–related three(s). The main taxons of the triology are the interdependent and independently related three values, variables, and/or units that are collectively identified as follows: “a”, “b”, and “c”. The taxon of triology has the following cohesive definition mathematically defined in set: {[a] ≠ [b] ≠ [c]}.
In the science of triology, the previously identified and mathematically defined “primary trichotomous taxonomy” is directly derived from the mathematical “Law of Trichotomy”. In terms of mathematics, Apostol in his book on calculus defined “The Law of Tricohotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers a and b, exactly one of the relations a < 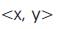 satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012) .
satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric (Sensagent, 2012) .
The foundational idea of a “Trichotomy” has a detailed long history that is based on discussions surrounding higher cognition, general thoughts, and descriptions of intellect. Philosopher Immanuel Kant adapted the Thomistic acts of intellect in his trichotomy of higher cognition.
which he correlated with his adaptation in the soul's capacities:
The Total Transformative Trichotomous – Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. The advantage of this research procedure is that it is a comprehensive holistic testing methodology that is designed to be a static way of holistically measuring categorical variables directly applicable to educational and social behavioral environments, where the established methods of pure experimental designs are easily violated. The unchanging base of the Tri–Squared Test is the 3 × 3 Table based on Trichotomous Categorical Variables and Trichotomous Outcome Variables. The emphasis of the three distinctive variables provide a thorough rigorous robustness to the test that yields enough outcomes to determine if differences truly exist in the environment in which the research takes place (Osler, 2013a).
The term “Triadic” literally means “having three units or parts”. Therefore, the first three “analytically–based” Topological [emphasizing identification] sequential Triological levels of the science of a Triology that make up the beginning of the process of Triological Scientific Analysis in terms of “discovery” consists of the following
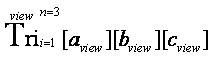 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively.  [the last part of the equation represents the “Triological Trine Triview Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a)];
[the last part of the equation represents the “Triological Trine Triview Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a)];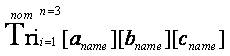 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively.  [the last part of the equation represents the “Triological Trine Trinominal Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and
[the last part of the equation represents the “Triological Trine Trinominal Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and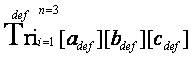 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively. [the last part of the equation represents the “Triological Trine Tridefine Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c) ].
[the last part of the equation represents the “Triological Trine Tridefine Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c) ].The term “Tripartite” literally means “shared by or involving the number three thereby consisting of three parts”. Consequently, the second three “assessment–focused” Taxonomical [emphasizing arrangement] sequential Triological levels of the science of a Triology that make up the midpoint of the process of Triological Scientific Analysis in terms of “organization” consists of the following:
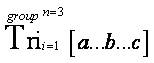 this particular mathematical Triological Notation is mathematically defined cumulatively, collectively, and comprehensively.
this particular mathematical Triological Notation is mathematically defined cumulatively, collectively, and comprehensively.  [the last part of the equation represents the “Triological Trine Tricluster Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a) ];
[the last part of the equation represents the “Triological Trine Tricluster Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a) ];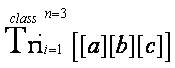 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively.  [the last part of the equation represents the “Triological Trine Triclassify Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and
[the last part of the equation represents the “Triological Trine Triclassify Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and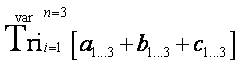 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively.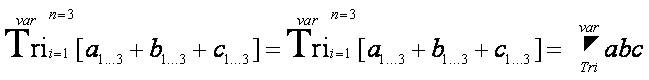 [the last part of the equation represents the “Triological Trine Trichotomy Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c)].
[the last part of the equation represents the “Triological Trine Trichotomy Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c)].The term “Triplex” literally means “systems having three parts provided or fitted in triplicate so as to ensure reliability”. Thus, the third three “advanced–insightful” Theological [emphasizing origin] sequential Triological levels of the science of a Triology that make up the final completions of the process of Triological Scientific Analysis in terms of “metaphysics” consists of the following:
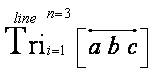 this particular mathematical Triological Notation is mathematically defined cumulatively, collectively, and comprehensively.
this particular mathematical Triological Notation is mathematically defined cumulatively, collectively, and comprehensively.  [the last part of the equation represents the “Triological Trine Triclinear Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a)];
[the last part of the equation represents the “Triological Trine Triclinear Triangulation Formula” from the “Trine Mathematical Operator” that appeared as a closed notation in the research article entitled “Transformational Research Engineering: Research Design Metrics for In–Depth and Empowering K–12 Teacher Professional Development” (Osler, 2013a)];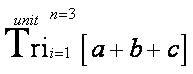 is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively. the last part of the equation represents the “Triological Trine Triunity Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and
the last part of the equation represents the “Triological Trine Triunity Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments” (Osler, 2013b)]; and is mathematically defined cumulatively, collectively, and comprehensively.
is mathematically defined cumulatively, collectively, and comprehensively. 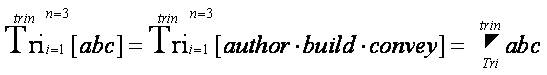 the last part of the equation represents the “Triological Trine Trichotomy Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c) ].
the last part of the equation represents the “Triological Trine Trichotomy Triangulation Formula” from the “Trine Mathematical Operator” that appeared as an open notation in the research article entitled “Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test” (Osler, 2013c) ].The following Triological mathematical formulae are written in Triological Mathematical notation which is of the form:
based upon the Triological Level and a specifically identified area. Holistically all nine Triology areas (or arenas) that indicate each triological level area of the study of cycles of thought, learning, life, and nature through triplicate structural, hierarchical, and sequential levels of topology, taxonomy, and theology are mathematically written as
Tri–Square or Tri–Squared comprehensively stands for “The Total Transformative Trichotomous – Squared Test” (or “Trichotomy–Squared”). It provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. Many statistical measures used in education are experimental research designs that require strict scientific methodologies that cannot be implemented in educational institutions without violating legal policies or severely disturbing the learning environment and associated instructional climate and vital to instruction. The time has come for education to provide its own scientific field and subsequent measures based on its own rigor and grounded in the foundation of longstanding educational research, fundamental educational theory, and innovations in qualitative, quantitative, and mixed methods research designs native to the specifics of pedagogy and andragogy (Osler, 2012).
The following definition of Tri–Squared (and subsequent narrative) was first presented by the author in a 2012 Journal on Mathematics research article. “Tri–Squared comprehensively stands for “The Total Transformative Trichotomous – Squared Test” (or “Trichotomy – Squared”). The Total Transformative Trichotomous – Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. The advantage of this research procedure is that it is a comprehensive holistic testing methodology that is designed to be a static way of holistically measuring categorical variables directly applicable to educational and social behavioral environments where the established methods of pure experimental designs are easily violated. The unchanging base of the Tri–Squared Test is the 3 × 3 Table based on Trichotomous Categorical Variables and Trichotomous Outcome Variables. The emphasis the three distinctive variables provide a thorough, rigorous robustness to the test that yields enough outcomes to determine if differences truly exist in the environment in which the research takes place (Osler, 2012).”
To effectively use Tri–Squared in a research investigation, one must first develop a series of trichotomous categorical variables based on associated trichotomous associated outcomes. This is the first initial and crucial step to using Tri–Squared as a valid, reliable, and objective means of analyzing data. Second, an “Inventive Investigative Instrument” must be created and implemented based on the initial trichotomous categorical variables and outcomes. This insures that the research investigation is consistent throughout the study and that the later Tri–Squared computations are validly reporting what actually took place in the investigative environment during the research study. The “Inventive Investigative Instrument” can be psychometrically delivered as a test, qualitatively delivered in the form of a research questionnaire, survey, interview or other form of metric. As long as the trichotomous categorical variables are measured according to the established associated trichotomous outcomes, then the research has merit within the confines and strict requirements of the Tri–Squared Test.
The Tri–Squared statistic transforms qualitative data into quantitative data and then measures the difference between the two to determine the validity of the initial research hypothesis. If no relationship is determined to exist between the qualitative and quantitative trichotomous categorical and outcome variables, then the Tri–Squared statistic equals zero. Adversely, the greater the relationship between the variables, the greater the value will be of the final Tri–Squared calculation. Statistics by nature is a methodical and selective science that requires specific and precise steps and is cautious in dealing with uncertainty. Thus, Tri–Squared is very comprehensive in its structure taking into account: number of measures, accountability through trichotomous metrics, precision in effect size, specified in sample size, and strict methodology in hypothesis testing (Osler, 2012a).
Tri–Squared is grounded in the combination of the application of the research by two mathematical pioneers and the author's research in the basic two dimensional foundational approaches that ground further explorations into a three dimensional Instructional Design (Osler and Waden, 2012). The aforementioned research includes the original dissertation of optical pioneer Ernst Abbe who derived the distribution that would later become known as the chi square distribution and the original research of mathematician Auguste Bravais who pioneered the initial mathematical formula for correlation in his research on observational errors. The Tri–Squared research procedure uses an innovative series of mathematical formulae that do the following as a comprehensive whole:
The process of designing instruments for the purposes of assessment and evaluation is called “Psychometrics”. Psychometrics is broadly defined as the science of psychological assessment (Rust & Golombok, 1989). The Tri–Squared Test pioneered by the author, factors into the research design a unique event–based “Inventive Investigative Instrument” (Osler, 2013d). This is the core of the Trichotomous – Squared Test. The entire procedure is grounded in the qualitative outcomes that are inputted as Trichotomous Categorical Variables based on the Inventive Investigative Instrument (Osler, 2013e). Osler (2012a) initially defined the Tri–Squared mathematical formula in the Journal on Mathematics article entitled, “Trichotomy – Squared – A novel mixed methods test and research procedure designed to analyze, transform, and compare qualitative and quantitative data for education scientists who are administrators, practitioners, teachers, and technologists” as follows: The Tri–Squared Model (in tabular format) and its associated calculations, definitions, procedures are explained in detail on the pages that follow. Table 1 follows and illustrates the Tri2 Mathematical Model illustrated in Tabular Format.
Table 1. Tri–Squared Test 3 × 3 Table Calculations
Table 1 illustrates the “Tri–Squared Test Model”; displays the “Standard Tri2 Test 3 × 3 Table”; and mathematically defines the corresponding “Tri–Squared Test Table Calculations”. This thereby explains how the “Tri2 Test Statistical Mathematical Model” is constructed, displaying the 3 × 3 Table calculation values of qualitative outcomes of the Tri–Squared Test. The qualitative values from this Table are directly derived from the outcomes of a triologically created research Inventive Investigative Instrument.
Table 2 determines the research alpha level and the Tri–Squared test hypothesis test critical value all based upon the research sample size. Table 3 determines the Tri-Squared probability. Table 4 follows and illustrates the Tri2 Test Total Calculations by Cell, Row, and Column illustrated in Tabular Format to explain how the Trichotomous – Squared Test is calculated. Table 5 displays sample data in a Tri–Squared Analysis with computational model and calculation sample data results. Lastly, Table 6 provides the explicative Tri–Squared Table calculation mathematical formulae in a tabular format for the purposes of clarity.
Table 4 is a Trichotomous – Squared Standard Three by Three Table designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a1, a2, and a3 . The 3 × 3 Table has the following Trichotomous Outcome Variables: b1 ; b2 ; and b3 . The Sample Total Calculations are conducted as in the table.
Table 4. A Tri2 3 × 3 Standard Table of Statistically Significant Tri2 Test Total Calculations by Cell, Row, and Column
Tri–Squared Qualitative Outcomes [Trix ]: A Sample Tri–Squared Test illustrating the Standard 3 × 3 Trichotomy–Squared Formula and Table of Outcomes reporting Qualitative Input Results using the Tri–Squared 3 × 3 Format: The sample data analyzed using the “Trichotomous T–Square Three by Three Table” designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a1 = Cognitive [Knowledge]; a2 = Affective [Dispositions]; and a3 = Psychomotor [Skills]. The 3 × 3 Table has the following Trichotomous Outcome Variables: b1 = Affirmative [Yes]; b2 = Negative [No]; and b3 = Inapplicable [or Irrelevant]. The Inputted Qualitative Results are reported as in Table 5.
Note:
When reporting the outcomes of the Tri–Squared Test, the Row and Column Totals are not presented. They are displayed in the Standard 3 × 3 Table for the purposes calculation clarity.
The Tri–Square Test Formula for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to determine the Validity of the Research Hypothesis:
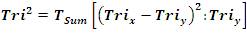
Degrees of Freedom (d.f.) for Tri–Squared: [R – 1][C – 1] = [3 – 1][3 – 1] = 4 = Tri2[x] .
Tri2 Critical Value Table = 8.180 (with d.f. = 4 at α = 0.10). For d.f. = 4, the Critical Value for p > 0.10 is 7.779. The calculated Chi–Square value is 8.180, thus we can reject the null hypothesis (H0 ) by virtue of the hypothesis test which yields the following: Critical Value of 7.779 < 71.57, the Calculated Value.
Tri–Squared Quantitative Outcomes [Triy ]: A Sample Tri–Squared Test illustrating the Standard 3 × 3 Trichotomy – Squared y Formula and Table of Outcomes reporting the Methodology used to calculate Quantitative Outcome Results using the Tri–Squared 3 × 3 Format is given in Table 6.
Sample Data analyzed using the Trichotomous T–Square Three by Three Table designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a1 = Cognitive [Knowledge]; a2 = Affective [Dispositions]; and a3 = Psychomotor [Skills]. The 3 × 3 Table has the following Trichotomous Outcome Variables: b1 = Affirmative [Yes]; b2 = Negative [No]; and b3 = Inapplicable [or Irrelevant]. The Outputted Quantitative Outcomes are determined as in Table 6.
The Tri–Square Test Formula for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to determine the Validity of the Research Hypothesis:
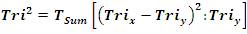
Degrees of Freedom (d.f.) for Tri–Squared: [R – 1][C – 1] = [3 – 1][3 – 1] = 4 = Tri2[x]
The second Table is necessarily reported in the final data. It is presented here only for the purposes calculation clarity. The next section details advanced Triology as the discipline of “Triostatistics”. Triostatisticsis the “post hoc” (or research studies that occur after the initial research has been conducted) measurements that can be conducted immediately following a statistically significant Tri–Squared Test.
Triostatistics (or more simply “Triostat”) is the application of Post Hoc measures to the outcomes of the Trichotomous Squared Test. As a statistical discipline, Triostat concerns the development and application of specific and uniquely designed advanced Post Hoc statistical tests, methodologies, and techniques. Triostat is used to further investigate the research outcomes from initially statistically significant Tri–Squared Tests. Research studies that analyze data through the use of theTrichotomous Squared Test are the foundation for Triostatistics. Thus, Triostatistics is the further investigation and precise in–depth study of the dynamic data that is the statistically significant Tri–Squared Test results (Osler, 2014a).
The word “Triostatistics” is a portmanteau of the terms: “Trichotomous” and “Statistics”; that can also be referred to as “Triostat”, “Advanced Trichometry, Trichometrics or Trichotometrics” or “The Science of Trichometry”. More definitively, Triostatistics is a branch of the science, statistics that is the specific application of statistical methods, techniques, and strategies to a wide range of topics that concern the Tri–Squared Test. At the heart of this, statistical discipline is the application of the mathematical “Law of Trichometry”. The science of Triostatistics encompasses the design of Tri–Squared experiments, especially in education and social behavioral settings. However, the utility and flexibility of Triostat as a body statistical metrics allows it to be applied to a variety of sciences (through the use and application of the mathematical “Law of Trichotomy”). Triostatistics as a discipline is the collection, summarization, and analysis of data from Tri–Squared experiments; and the interpretation of, and inference from, statistically significant Tri–Squared Test results (Osler, 2014a).
Triostatistics have their foundation in the analysis of initially statistically significant Tri–Squared Tests. Triostatistical measures are all grounded in Trichotomous – Squared research methods. They extend that methodology into novel statistical metrics that provide “Triostatisticians” detailed information on a variety of quantitative analytical areas. These areas are or are identified as: the relationships between Tri–Squared variables, the variable parameters of trichotomous variant, the transformation of trichotomous data into inferential metrics and/or measures, and a host of other post hoc statistical areas. The Triostatistical procedures that provide more insight into the Tri–Squared Test are as follows:
An Omnibus Test is a global or overall test of a given statistic. Tri–Squared Post Hoc Tri–Symmetrical Omnibus Tests have two distinctive metrics in the form of Dichotomous Analytical statistical measurement procedures:
Tri–Correlational Analytics are based upon small sample sizes and can only be used with small Tri–Squared interval effect sizes. Tri–Associative Analytics are applicable to any size Tri–Squared Test as long as a level of statistical significance has first been established in an initial research study (an established Tri–Squared level of statistical significance is also true of Tri–Correlational Analytical statistical measures) (Osler, 2014f). The two branches of Tri–Squared Post Hoc Tri–Symmetrical Omnibus Tests are defined as follows: Tri–Correlational Analytics: [Trir ] and Tri–Associative Analytics:  . Tri–Correlational Analytics [Trir ] are statistically defined as an omnibus methodology that includes statistical post hoc testing to determine the value of a significant small sample sized Tri–Squared Test. Tri–Associative Analytics
. Tri–Correlational Analytics [Trir ] are statistically defined as an omnibus methodology that includes statistical post hoc testing to determine the value of a significant small sample sized Tri–Squared Test. Tri–Associative Analytics are defined as a dual Omnibus Statistical Test methodology that includes two statistical post hoc tests to determine more detailed information on the value and significance of the relationships between the Categorical and Outcome Variables of a significant Tri–Squared Test (Osler, 2014a).
are defined as a dual Omnibus Statistical Test methodology that includes two statistical post hoc tests to determine more detailed information on the value and significance of the relationships between the Categorical and Outcome Variables of a significant Tri–Squared Test (Osler, 2014a).
The Trimetric Tri–Squared Test is designed to determine the Construct Validity of statistically significant Tri–Squared Inventive Investigative Instruments. In this case, Construct Validity is defined as: “The overall validity (or “truthfulness”) of the itemized inferences that the researcher designed Inventive Investigative Instrument purported to accurately and actually measure regarding the Trichotomous Categorical Variables that were under initial research investigation. To do this, the Trimetric Tri–Squared Test first uses the “Summative Post Hoc Tri–Squared Differential Operator”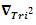 to determine the input and output mean differences from the initial Tri–Squared investigation. Tri–Squared Differential Operator does this by converting the input and output mean differences into a new “Mean Difference 3 × 3 Tri–Squared Table” and conducts a Tri–Squared Test on the subsequent outcomes (Osler, 2014d). This is a sequential calculation that involves the summation of the initially inputted qualitative outcomes with their corresponding quantitative outcomes (via Matrix Algebra) and individually dividing them by the Total Number of Distributed Tri–Square Tests [nTri ] (Osler, 2014a).
to determine the input and output mean differences from the initial Tri–Squared investigation. Tri–Squared Differential Operator does this by converting the input and output mean differences into a new “Mean Difference 3 × 3 Tri–Squared Table” and conducts a Tri–Squared Test on the subsequent outcomes (Osler, 2014d). This is a sequential calculation that involves the summation of the initially inputted qualitative outcomes with their corresponding quantitative outcomes (via Matrix Algebra) and individually dividing them by the Total Number of Distributed Tri–Square Tests [nTri ] (Osler, 2014a).
Tri–Squared Mean Cross Comparative Analysis (or “TSMCCA”) is an advanced novel analysis metric designed to analyze the outcomes of the Tri–Squared Test. This methodology is referred to as: “Tri–Squared Mean Cross Comparative Analysis” (given the acronym TSMCCA). Tri–Squared Mean Cross Comparative Analysis involves the computation and in–depth study of means extracted from an initial Tri–Squared Test. The Tri–Squared Test had an established level of statistical significance that provided the grounds for further Post Hoc investigation. The TSMCCA statistic is an Advanced Post Hoc test of the transformative process of qualitative data into quantitative outcomes through the Tri–Squared Test first introduced in the Journal on Mathematics. Advanced statistical analytics are involved in the TSMCCA mathematical model that allows for critical analysis of mean scores on item results (Osler, 2013f). This type of in–depth post hoc statistical analysis permits a higher level of Tri–Squared meta–analytical investigative inquiry (Osler, 2014a).
Trivariant Analysis seeks to determine the differences in group means for Trichotomous Outcome Variables both externally and internally. The Trivariant or “Trichotomous Variation” can also be referred to as the “Trivariance” or “Trivariation”. Due to the invariant structure of Trichotomous Inventive Investigative Instruments (are always in a 3 × 3 tabular format), the mean comparisons are in column form. Trivariant Analysis is similar to a 3 × 1 factor ANOVA in its process of analyzing group means to determine a difference overall in treatment effects. In this case, the researcher is attempting to show the differences in the three Trichotomous Outcome Variables to validate the repeated measures, design of the post hoc significant Tri–Squared Inventive Investigative Instrument (which was designed and ultimately deployed based upon an overarching research question). In addition, the Trivariant Analysis research methodology also validates the differences in the post hoc 3 × 3 Standard Table mean on the external (between) and internal (within) Trichotomous Outcomes of the initially significant Tri–Squared Test (Osler, 2014a).
TRINOVA is an in–depth [Trichotomous Nomographical Variance] statistical procedure (Osler, 2014d)a for the internal testing of the transformative process of qualitative data into quantitative outcomes through the Tri–Squared Test first introduced in the Journal on Mathematics, and further detailed in the Journal on Educational Technology, Journal on School Educational Technology, and Journal on Educational Psychology. TRINOVA is an advanced statistical measure that is designed to check the validity and reliability of a Tri–Squared Test. This is a novel approach to advanced statistical post hoc Tri–Squared data analysis (Osler, 2014b). It adds considerable value to the mixed methods approach of research design that involves the holistic combination and comparison of qualitative and quantitative data outcomes (Osler, 2014a).
TRICOVA is a detailed statistical procedure for the internal testing of the outcomes of a significant transformation of qualitative data into quantitative outcomes through the Tri–Squared Test (first introduced in the Journal on Mathematics, and detailed further in the Journal on Educational Technology, Journal on School Educational Technology, and the Journal on Educational Psychology). TRICOVA as an advanced statistical procedure; is designed to measure the overall size of the movement between inputted and outputted Tri–Squared variables. It also is designed to identify the magnitude and type of covariant relationship in existence between Tri–Squared Test Qualitative and Quantitative Variables. This new innovative approach to the advanced statistical post hoc metrics of the Tri–Squared Test adds an additional layer of richness and insight into the inner workings of the Tri–Squared Test. It also adds considerable value to the mixed methods approach of research design that involves the holistic combination and comparison of qualitative and quantitative data outcomes (Osler, 2014a).
“Multiple Trichotomous Coefficient of Variation Analysis” statistic represented by the acronym [“MULTICOVA”] is an innovative, in–depth way of further investigating a statistically significant Post Hoc Tri–Squared Test. MULTICOVA is an advanced and detailed statistical procedure for the internal testing of the outcomes of the mixed methods Tri–Squared Test (first introduced in the Journal on Mathematics, and detailed further in the Journal on Educational Technology, Journal on School Educational Technology, and the Journal on Educational Psychology). MULTICOVA as an advanced statistical procedure; is designed to measure the “Trichotomous Coefficient of Variation” of inputted and outputted Tri–Squared variables (Osler, 2015b). The Trichotomous Coefficient of Variation is also a normalized measure of a trichotomous probability distribution or trichotomous frequency distribution. This new statistic is an innovative approach to the sequential series of advanced post hoc Tri–Squared Test statistical metrics (Osler, 2014a).
In Tri–Squared statistics, Trichotomous Progression Analysis is a post hoc statistical method used for estimating the direction and nature of relationships among statistically significant Trichotomous Categorical and Outcome Variables. It includes many mathematical techniques for modeling and analyzing the results of initially significant Trichotomous Qualitative and Quantitative Variables, when the focus is on the relationship between a significant Trichotomous Quantitative Variable as [“y”] the Trichotomous Dependent Variable and the significant Trichotomous Qualitative Variable as the Trichotomous Independent Variable [“x”]. More specifically, Trichotomous Progression Analysis enables research investigators to determine how each of the recorded values of the Trichotomous Dependent Variable (or “Trichotomous Criterion Variable”) [“y”] changes when any one of the Trichotomous Independent Variables [“x”] varies. Trichotomous Progression Analysis also provides information on how the average values of the Trichotomous Dependent Variable vary or are fixed when the corresponding Trichotomous Independent Variables vary or are fixed. The graphed Cartesian Bi–Coordinate Line (for Trichotomous Variables x and y) that indicates the relationship between Trichotomous Qualitative and Quantitative Variables is the “Trichotomous Estimation Target” that is also a “Trichotomous Function of the Trichotomous Independent Variables” is referred to as the “Trichotomous Progression Function”. This function best illustrates the predictive relationship between the Trichotomous Dependent and Independent Variables (or Trichotomous Quantitative and Qualitative Variables). In Trichotomous Progression Analysis, the variation of the Trichotomous Dependent Variable around the Trichotomous Progression Function can be illustrated, and can be described by the Tri–Squared Probability Distribution. Trichotomous Progression Analysis is applicable for prediction and also for forecasting; where its outcomes can be used to accurately make conjectures about future Tri–Squared Test outcomes (if the significant Tri–Squared Test were to be replicated under the same conditions and circumstances). In summation, Trichotomous Progression Analysis is used to comprehend (through accurate, meticulous, and rigorous calculation) which significant Trichotomous Independent Variables are related to their respective Trichotomous Dependent Variables (Osler, 2014c). In gathering this data, researchers are able to explore the forms and predictive nature of the relationships between post hoc statistically significant Tri–Squared Test Trichotomous Variables (Osler, 2014a).
Trichotomous Comparative Oneness of Measurement [or TRICOM] takes the standard Trichotomous – Squared Test and applies it to functionally analyze a single case study. Thus, a TRICOM Test is a method used to conduct research on a single individual (n = 1). The power of the Test and its general applicability lies in the longitudinal repeated measurement of the researcher designed Trichotomous Inventive Investigative Instrument.
There are two forms of Repeated Measures in Trichotomously–Squared Inventive Investigative Instruments. They are: 1. “Iterative repetitive Trifold Trichotomous Categorical Variables” (a1 , a2 , and a3 ); and 2. “Nested Trifold Recursive Trichotomous Outcome Variables” (b1 , b2 , and b3 ). “Iteration” is generally defined as the act of process repetition with the aim of reaching a desired target, goal, and/or result. Sequentially, each subsequent “iterate” (individual iteration) is a repetition of the process. The outcome of an individual iteration is used as the starting point for the iteration that immediately follows. In the case of Tri–Squared research instruments, the term “Iteration” refers to breakdown of the overall overarching investigation research question into three specific Categorical Variables so that it can be accurately measured. The results of these variables will clearly statistically state whether or not the initial research question has merit. “Recursion” is broadly defined as the process of repeating items in a self–similar way. For example of this process, consider an illustration that contains multiple or infinite smaller and smaller nested identical images that repetitively occur over and over (as an identical image within an image within an image, etc.) (Osler, 2015a). The term is applicable to the Tri–Squared researcher designed instrument, in that it describes the threefold repetition of the structure of the Trichotomous Categorical Variable sub–questions that are each extracted from the three Categorical Variables (this thereby provides an Inventive Investigative Instrument that has a grand total of nine Trichotomous Outcomes nested within three interrelated, but distinctively specific Trichotomous Categorical Variables and the tabulated results of which create the Standard 3 × 3 Tri–Squared Table) (Osler, 2014a) .
Tri–Center Analysis is a measurement of the central tendency data of a statistically significant Tri–Squared Test. The metric as a statistic is designed to analyze the Post Hoc outcomes of the Tri–Squared Test using the traditional parametric statistical measures of central tendency [The Trichotomous Mean, Mode, and Median, respectively]. This methodology is referred to as: “Tri–Center or Tri–Central Analysis”. Tri–Center Analysis involves the computation of normal distribution parametric measures to examine the values of an independent statistically significant Tri–Squared Test. The Tri–Squared Test values are considered to be a representation of a holistic series of sequential within group Trichotomous results.
The following calculations are the basis of Tri–Center Analysis. They consist of the traditional statistical “measures of center” or “measures of central tendency”. They are represented in terms of Trichotomous relations in the following manner:
Calculating the Tri–Squared Test Mode =Tri2 [MO] which represents the most frequently occurring numerical value in the set of data; and
To calculate the spread and variation of Tri–Squared Test results the researcher will need a set of mathematical conventions and specific Trichotomous statistical formulae which use those conventions to determine the Trichotomous Variance and Standard Deviation, respectively (Osler, 2014a) .
Trichotomous Cubed (or “Tri–Cubed”) Tri–Coordinate Meta–Analysis is an advanced highly precise research methodology for the accurate in–depth analysis of existing reported data on a specifically identified criterion. The Tri–Cubed Test integrates the Tri–Squared Test in a Tri–Coordinate [x, y, and z] data analysis methodology involves a variety of robust rigorous calculations and detailed computations to provide further insight on the inner workings of reported and/or statistically significant data. A dynamic and complex third trichotomous variable (the Trichotomous Algorithmic Variable or “TAV)” is factored into the data analysis and calculation procedures of the Tri–Squared Test producing the Tri–Coordinate nature of the Tri–Cubed Test. The Tri–Cubed methodology uses the Isometric Cuboid mathematical geometric model from Visualus (Osler, 2010).
The Trichotomous – Cubic Parametric Model (collectively abbreviated as “TRIMOD”) is a rigorous post hoc mathematical data analysis methodology designed to more accurately detail the outcomes of a statistically significant Tri–Squared Test. TRIMOD infuses the Tri–Cubed Test model with the Tri–Squared Test in a detailed sequential Tri–Coordinate series of x, y, and z planar vectors native to the Visualus Isometric Cuboid (Osler, 2010). A series of methodical mathematical calculation procedures are then conducted to yield the Tri–Cubic Parametric Model outcomes (Osler, 2014a).
MANOVA is an acronym for “Multiple Analysis of Variance” also called “Multivariate Analysis of Variance”. It is a statistical procedure for the multivariate analysis of multiple groups of data with two or more dependent or outcome variables. Multivariate Analysis of Variance is also an advanced statistical test procedure for comparing the multivariate population means of several groups. As a unique multi–group procedure, it is most commonly used in research designs when there are two or more outcome variables associated with multiple within and between group means in a specified research setting (the vast majority of statistical studies that use the MANOVA procedure provide a set of individual probability values for each outcome variable in order to test for specific levels of statistical significance). MANOVA is often used to answer the following research questions:
When analyzing multiple groups of data, the inferential statistical measure of variance (or the spread of scores around the distribution mean) is a more accurate method of analyzing data than the more traditionally used inferential rectilinear Standard Deviation (the square root of the Variance) statistic. There are multiple forms of group data analysis in traditional statistical procedures. These measures, include: ANOVA (“Analysis of Variance”), the standard statistical metric used to analyze multiple group means), ANCOVA (“Analysis of Covariance”), the statistical test used to measure pre and post outcomes for multiple groups and their associated group means), and MANOVA (the aforementioned “Multiple Analysis of Variance”), which is designed to analyze and provide feedback on multiple group means and their associated outcome variables). Similar to the previously listed multiple methods of group data analysis (that greatly depend upon the research design and methodology used by the researcher in deciding exactly how to analyze group data at the outset of research), Triostatistics are a series of post hoc research methods (that are uniquely grounded in the statistical significance of an initial Tri–Squared Test) (Osler, 2014a).
The comprehensive model provided in this narrative illustrates an epistemological rational for a novel science that can be measured via trichotomous statistical analysis metrics. As detailed at the beginning of this paper, “Triology” is the study of the trifold nature of natural phenomena. Triology is measured then through its foundation in the mathematical “Law of Trichotomy”. The mathematical “Law of Trichotomy” is observable throughout nature. As such, one is then able to conduct scientific research on a variety of topics using said law. The method of measurement presented here is defined as the field of “Triostatistics” (Osler, 2014a). Triostatistics is grounded in the mathematical Tri–Squared Analysis procedure known as the “Tri–Squared Test”. Many of the triostatistical measures were listed before this section. There are currently over twenty-eight different triostatistical measurement methods that are accessible to research investigators. This plethora of “triological statistical tests and techniques” has its foundation in the “science of triology”. Thus, the primary model used to conduct scientific triological research is the Tri–Squared Analysis procedure that uses the Tri–Squared Test that exemplifies the science of “Triology”. This thereby validates the triological research triostatistical analysis methodology as the ideal model of triological science.
The new science of “Triology” opens new doors to the study and analysis of nature and natural phenomena. Triology with its engaging and dynamically empowering methodology enables researchers to further explore the intricacies and inner workings of natural phenomena from new perspectives. Such insight will provide information that in turn provides innovative solutions to existing and emerging problems. Triological scientific measurements, such as the Tri–Squared Test and the novel post hoc field of Triostatistics add both breadth and depth to research thereby allowing for more invention, exploration, and discovery. As stated in 2014 in the Kentucky Journal of Excellence in College Teaching and Learning, “There are a number of Triostatistical metrics and tests that can provide additional information on statistically significant Tri–Squared research investigations that can greatly enhance the understanding of initial research results. The post hoc use of Triostatistics on statistically significant Tri–Squared Test data provides a series of plausible statistical measures that allow research investigators to further interpret the in–depth and rich complexities of Tri–Squared research data (Osler, 2014a).” The growing use of this new science will create variety of new research in many fields as researchers and scientists collaborate and share the outcomes of their investigations. In this manner, learning grows and becomes more appealing, approachable, acceptable, functional, and practical. Thus, triology as a science offers a novel thought process that provides a new lens to look at and explore the world.