In 1963, J .C. Kelly [6] introduced the concept of bitopolgical space. N. Levine [9] introduced the idea of semi open sets and semi continuity and Mashhour, et al. introduced the concept of pre open sets and pre continuity in a topological space. M. Jelic [4] generalized the idea of pre open sets and pre continuity in bitopological space. S.N. Maheshwari and Prasad [10] introduced semi-open sets in bitopological spaces and further properties of this notion were studied by Bose [1] in 1981. F.H. Khedr, S.M. Al-Areefi and T. Noiri [7] generalized the notion of semi pre open sets to bitoplogical spaces and semi pre continuity in bitopological spaces. B.K. Lahiri and P. Das [2] studied semi open sets in a space. Yiezi Kadham Mahdi [11] introduced new definition of semi-open sets and semi closed set in bitopological spaces. A. Kar and P. Bhattacharyya [5] studied pre open sets and pre continuity in bitopological space. Tri topological space is a generalization of bitopological space. The study of tri-topological space was first initiated by Martin M. Kovar[8]. S. Palaniammal [12] studied tri topological space. N.F. Hameed and Moh. Yahya Abid [3] gave the definition of 123 open set in tri topological spaces. The purpose of the present paper is to introduce tri semi open sets, tri pre open sets, tri continuity, tri semi continuity and tri pre continuity and their fundamental properties in tri topological space. In this paper, tri open set is used in place of 123 open sets.

1.1 Definition 1

Let X be a nonempty set and T₁ , T₂ and T₃ are three topologies on X. The set X together with three topologies is called a tri topological space and is denoted by (X, T₁ , T₂ , T₃ ) [12] .

1.2 Definition 2

A subset A of a topological space X is called 123 open set if A∈ T₁∪T₂∪ T₃ and complement of 123 open set is 123 closed set [3].

1.3 Definition 3

Let (X, P₁, P₂) be a bitopological space then a subset A of X is said to be semi-open set if A ⊆cl_pi (int_pi(A)) for i = 1 or 2 and complement of semi open set is semi-closed [11].

1.4 Definition 4

Let (X, P₁,P₂) be a bitopological space then, a subset A of X is said to be Pre open set if A⊆int_pi (cl_pi(A)) for i = 1 or 2 and complement of Pre open is Pre- closed [11].

1.5 Definition 5

A function f from a bitopological space (X, P₁,P₂ ) into a bitopological space (Y, W₁,W₂ ) is called continuous if and only if f^-1(V) is pi-open set (pi-closed set) in X for each wi- open set (wi-closed set ) in Y and it is called semi continuous if f^-1(V) is semi open (semi-closed) set for each pi-open (pi-closed) set V in Y [11].

2.1 Definition 6

Let (X, T₁ , T₂ , T₃ ) be a tri topological space and (Y, T₁', T₂’, T₃’) be another tri topological space.

A function f : X→Y is called a tri continuous function if f ^-1(V) is tri open in X, for every tri open set V in Y.

Example 1: Let, X={a,b,c}  T₁={X,φ,{a}}, T₂={X,φ,{a,b}}, T₃={X,φ,{b}}

Open sets in tri topological spaces are union of all three topologies.

Tri open sets of X={X,φ,{a},{a,b},{b}}.

Let Y={1,2,3},  W₁={Y,φ}, W₂={Y,φ, {2}}, W₃={X,φ,{1}{1,2}}

Tri open sets of Y={Y,φ,{1},{2},{1,2}}.

Consider the function ƒ: (X,P₁,P₂,P₃)→ (Y,W₁,W₂,W₃)is defined as,

ƒ^-1{1}={b} ,ƒ^-1{2}={a},ƒ^{- 1}{1,2}={a,b}, ƒ^-1(φ)= φ, ƒ^{- 1}(Y)=X

Here the inverse image of each tri open set in Y under f is tri open set in X. Hence f is tri continuous function.

2.2 Theorem 1

A function ƒ: (X,P₁,P₂,P₃) → (Y,W₁,W₂,W₃) is tri continuous if and only if the inverse image of every tri open set in Y is tri open in X.

Proof: (Necessary): Let ƒ: (X,P₁,P₂,P₃)→ (Y,W₁,W₂,W₃) be tri continuous function and U be any tri open set in Y. Then Y-U is tri closed in Y. Since f is tri continuous function, ƒ^-1(Y-U) = X - ƒ^{- 1}(U) is closed in X and hence ƒ^-1(U) is tri open in X.

(Sufficiency): Assume that f^-1(V) is tri open in X for each open set V in Y. Let V be a closed set in Y. Then Y - V is open in Y. By assumption f^-1(Y-V) = X -f^-1(V) is tri open in X which implies that f^-1(V) is tri closed in (X, T₁ , T₂ , T₃ ). Hence f is a tri continuous function.

2.3 Theorem 2

Let (X, T₁ , T₂ , T₃ ) and (Y, W₁ , W₂ , W₃ ) be two tri topological space. Then,

f : X → Y is a tri continuous function if and only if f^-1(V) is tri closed in X whenever V is tri closed in Y.

2.4 Theorem 3

Let (X, T₁ , T₂ , T₃ ) and (Y, W₁ , W₂ , W₃ ) be two tri topological space. Then, f : X →Y is a tri continuous function if and only if f (cl(A)) ⊂cl(f(A)) A⊂X.

Proof: Suppose f : X→ Y is tri continuous function. Since cl[f (A)] is tri closed in Y. Then by theorem (2), f^-1[cl(f(A))] is tri closed in X,

[1]

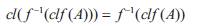
Now: ƒ(A)⊂cl(ƒ(A)), A⊂f^-1(ƒ(A)) ⊂ƒ^-1(clƒ(A))

Then cl(A)⊂cl(ƒ^-1(clf(A))) = ƒ^-1 (clƒ(A)) by (1).

Then ƒ(cl(A))⊂cl(ƒ(A)).

Conversely, Let ƒ(cl(A))⊂cl(ƒ(A)) A⊂X

Let F be tri closed set in Y so that cl(F) = F. Now f^-1 (F)⊂ X, by hypothesis,

     f(cl(f^-1(F))) ⊂ cl(f(f^{- 1}(F)) ⊂ cl(F) = F

Therefore, cl(ƒ^-1(F) ⊂ ƒ^-1(F). But ƒ^-1(F)⊂cl(ƒ^-1(F)) always.

Hence  cl(ƒ^-1(F) = ƒ^-1(F) and so f^-1(F) is tri closed in X.

Hence by theorem (2) f is a tri continuous function.

2.5 Theorem 4

Let (X, T₁ , T₂ , T₃ ) and (Y, W₁ , W₂ , W₃ ) be two tri topological spaces. Then, f : X→ Y is tri continuous function if and only if cl (ƒ^-1(B) ⊂ ƒ^-1(cl(B)) B⊂ Y

Proof: Suppose f : X →Y is tri continuous. Since cl(B) is tri closed in Y, then by theorem (2), f^-1(cl(B)) is tri closed in X and therefore,

[2]

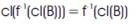
Now, B⊂ cl(B), then f^-1(B)⊂ f^-1(cl(B)), then cl(ƒ^-1(B) ⊂ cl(f^-1(cl(B))) = ƒ^-1(clB)  by (2)

Conversely: Let the condition hold and let F be any tri closed set in Y so that cl(F) = F. By hypothesis, cl(f^-1(F))⊂f^{- 1}(cl(F)) = f^-1(F). But f^-1(F)⊂ cl (f^-1(F)) always. Hence cl(f^-1(F)) = f^-1 (F) and so f^-1(F) is tri closed in X. It follows from theorem (2) that f is a tri continuous function.

2.6 Theorem 5

Let (X, T₁ , T₂ , T₃ ) and (Y, W₁ , W₂ , W₃ ) be two tri topological spaces. Then, f : X→ Y is a tri continuous function if and only if ƒ^-1(int(B))⊂ int(f^-1(B))  B⊂Y

Proof: Let f : X →Y be a tri continuous. Since int(B) is tri open in Y, then by theorem (1), f^-1(int(B)) is tri open in X and therefore,

[3]

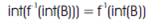
Now, int(B)⊂ B, then f^-1(int(B))⊂ f^-1 (B), then int(f^-1(int(B)))⊂ int(f^-1(B)) by (3)

Conversely: Let the condition hold and let G be any tri open set in Y so that int(G) = G. By hypothesis, f^-1(int(G))⊂ int f^-1(G). Since f^-1(int(G)) = f^-1(G) then f^-1(G) ⊂int(f^-1(G)), but int(f^-1 (G))⊂ f^-1(G) always and so int(f^-1(G)) = f^-1(G). Therefore f^-1(G) is tri open in X. Consequently by theorem (1) f is a tri continuous function.

3.1 Definition 7

Let (X, P₁ , P₂ , P₃ ) be a tri topological space then a subset A of X is said to be tri semi-open set if A ⊆cl(int(A)) and complement of tri semi open set is tri semi- closed. The collection of all tri semi open sets of X is denoted by SO (X).

Example 2: Let X={a,b,c} , T₁={X,φ,{a}}, T₂={X,φ,{a,b}}, T₃={X,φ,{a,c}}

Open sets in tri topological spaces are union of all three topologies.

Tri open sets of X={X,φ,{a},{a,b},{a,c}}

Tri semi open set of X is denoted by S O(X) = X={X,φ,{a},{a,b}, {a,c}}

3.2 Definition 8

Let (X, P₁ , P₂ , P₃ ) be a tri topological space then a subset A of X is said to be tri pre open set if A ⊆int(cl(A)) and complement of tri pre open set is tri pre-closed. The collection of all tri semi open sets of X is denoted by PO(X).

Example 3: Let X={a,b,c} , T₁={X,φ,{a}}, T₂={X,φ,{a,b}}, T₃={X,φ,{b,c}}

Open sets in tri topological space are union of all three topologies.

Then tri open sets of X={X,φ,{a},{a,b},{b,c}}

Pre open sets of X is denoted by P O(X) = X={X,φ,{a},{a,b}, {b,c}}

Remark [8]: Note that tri open sets of X need not be necessarily from a topology on X.

3.3 Definition 9

Let (X, P₁ , P₂ , P₃ ) be a tri topological space. Let A⊂ X. An element x ∈A is called tri semi interior point of A, if there exist a tri semi open set V such that x∈ V ⊂A. The set of all tri semi interior points of A is called the tri semi interior of A and is denoted by s int(A).

3.4 Definition 10

Let (X, P₁ , P₂ , P₃ ) be a tri topological space. Let A ⊂X. An element x∈ A is called tri pre interior point of A, if there exist a tri pre open set V such that x∈ V ⊂A. The set of all tri pre interior points of A is called the tri pre interior of A and is denoted by p int (A).

3.5 Theorem 6

Let A ⊂X be a tri topological space. s int(A) is equal to the union of all semi open sets contained in A.

Note: 1. p int(A) ⊂A.

          2. p int(A) is semi open sets.

3.6 Theorem 7

s int(A) is the largest semi open sets contained in A.

3.7 Theorem 8

A is semi open if and only if A = s int(A)

3.8 Theorem 9

s int(A∪B) ⊃s int A∪s int B.

3.9 Definition 11

Let (X, P₁ , P₂ , P₃ ) be a tri topological space. Let A⊂ X. The intersection of all tri semi closed sets containing A is called a tri semi closure of A and is denoted as scl(A).

Note: Since intersection of tri semi closed sets is tri semi closed set, scl(A) is a tri semi closed set.

Note: scl(A) is the smallest tri semi closed set containing A.

3.10 Theorem 10

A is tri semi closed set if and only if A = scl(A).

3.11 Theorem 11

Let A and B be subsets of (X, T₁ , T₂ , T₃ ) and x∈ X.

• A is tri pre closed if and only if A = pcl(A)
• If A ⊂B, then pcl(A) ⊂pcl(B).
• x ∈ pcl(A) if and only if A∩ U≠φ for every tri pre open set U containing x.

3.12 Theorem 12

Let A be a subsets of (X, T₁ , T₂ , T₃ ), if there exist an tri pre open set U such that A ⊂U ⊂cl(A), then A is tri pre open.

3.13 Theorem 13

In a tri topological space (X, P₁ , P₂ , P₃ ), the union of any two tri semi open sets is always a tri semi open set.

Proof: Let A and B be any two semi-open sets in X.

Now A∪B ⊆cl(int(A))∪cl(int(B))

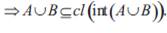Hence A∪ B tri semi open sets.

Remark: The intersection of any two tri semi open sets may not be a tri semi open sets as shown in the following example.

Example: Let X={a,b,c} , T₁={X,φ,{a}}, T₂= {X,φ,{a,b}}, T₃={X,φ,{b,c}}

Open sets in tri topological space are union of all three topologies.

Then tri open sets of X={X,φ,{a},{a,b},{b,c}}

Tri semi open set of X is denoted by S O(X) = X={X,φ,{a},{a,b}, {b,c}}

Here {a,b}∩{b,c} = {b} ∉ S O(X).

3.14 Theorem 14

If A is tri open sets then A is tri semi-open set.
Proof: Let A is tri open set.
Therefore A = int(A).

Now, A⊂cl(A) = cl(int(A)). Hence A is a tri semi-open set.

3.15 Theorem 15

Let A and B be subsets of X such that B⊆ A⊆ cl(B). If B is tri semi-open set then A is also a tri semi-open set.
Proof: Given B is tri semi-open set. so, we have B⊆cl(int (B)⊆cl(int(A)). Thus cl(B) ⊆ cl(int(A)). Hence A is also a tri semi-open set.

4.1 Definition 12

A function f from a tri topological space (X, P₁ , P₂ , P₃ ) into another tri topological space (Y, W₁ , W₂ , W₃ ) is called tri semi continuous if f^-1(V) is tri semi open set in X for each tri open set V in Y.

Example: Let, X={a,b,c} , T₁={X,φ,{a}}, T₂= {X,φ,{a,b}}, T₃={X,φ,{b,c}}

Open sets in tri topological spaces are union of all three topologies.
Then tri open sets of X = X={X,φ,{a},{a,b},{b,c}}.
SO(X) sets of X={X,φ,{a},{a,b},{b,c}}.
Let Y = {1, 2, 3}, W₁={Y,φ,{1,3}}, W₂= {Y,φ,{2}}, W₃={X,φ,{2},{1,2}}
Tri open sets of Y= {Y,φ,{2},{1,2},{1,3}}
SO(Y) sets of Y= {Y,φ,{2},{1,2},{1,3}}
Consider the function f : X →Y is defined as,
f^-1{2} = {a}, f^-1{1,2} = {a,b}, f^-1{1,3} = {b,c}, f^-1{ φ} = { φ}, f^-1{Y} = X.
Since the inverse image of each tri open set in Y under f is tri semi open set in X. Hence f is a tri semi continuous function.

4.2 Definition 13

A function f defined from a tri topological space (X, P₁ , P₂ , P₃ ) into another tri topological space (Y, W₁ , W₂ , W₃ ) is called tri pre continuous function if f^-1(V) is tri pre open set in X for each tri open set V in Y.
Example: Let  X={a,b,c} , T₁={X,φ,{a}}, T₂={X,φ,{a,b}}, T₃={X,φ,{b,c}}
Open sets in tri topological space are union of all three topologies.
Tri open sets of X={X,φ,{a},{b},{b,c}}

PO(X) sets of X={X,φ,{a},{b},{b,c}}

Let Y = {1,2,3}, W₁={Y,φ,{2}}, W₂={Y,φ, {3}}, W₃={X,φ,{1,3}}
Tri open sets of Y= {Y,φ,{2},{3},{1,3}}
SO(Y) sets of Y= {Y,φ,{2},{3},{1,3}}
Consider the function f : X →Y is defined as,
f^-1{2} = {a}, f^-1{3} = {b}, f^-1{1,3} = {b,c}, f^-1{φ } = { φ}, f^-1{Y} = X.
Since the inverse image of each tri open set in Y under f is tri pre open set in X. Hence f is a tri pre continuous function.

4.3 Theorem 16

Let f : (X, P₁ , P₂ , P₃ ) →(Y, W₁ , W₂ , W₃ ) be a tri pre continuous open function. If A is an tri pre open set of X, then f(A) is tri pre open in  Y.
Proof: First, let A be tri pre open set in X. There exist an tri open set U in X such that A ⊂U⊂ cl(A). Since f is tri open function then f(U) is tri open in Y. Since f is tri continuous function, we have f(A) ⊂f(U)⊂ f(cl(A))⊂ cl(f(A)). This show that f(A) is tri pre open in Y. Let A be tri pre open in X. There exist an tri pre open set U such that U ⊂A ⊂cl(U). Since f is tri continuous function, we have f(U) ⊂f(A)⊂ f(cl(U))⊂ cl(f(U)). By the proof of first part, f(U) is tri pre open in X. Therefore, f(A) is tri pre open in Y.

4.4 Theorem 17

Let f : (X, P₁ , P₂ , P₃ ) →(Y, W₁ , W₂ , W₃ ) be a tri pre continuous open function. If V is an tri pre open set of Y, then f^-1 (V) is a tri pre open  in X.
Proof: First, let V be tri pre open set of Y. There exist an tri open set W in Y, such that V ⊂W⊂ cl(V). Since f is a tri open set, we have  f^-1(V) ⊂f^-1(W)⊂ f^-1 (cl(V))⊂ cl(f^-1(V)). Since f is tri pre continuous, f^-1(W) is tri pre open set in X. By theorem 12, f^{- 1}(V) is a tri pre open set in X. The proof of the second part is shown by using the fact of first part.

4.5 Theorem 18

The following are equivalent for a function f : (X, P₁ , P₂ , P₃ ) (Y, W₁ , W₂ , W₃ )

• f is tri pre continuous function;
• the inverse image of each tri closed set of Y is tri pre closed in X;
• For each x∈ X and each tri open set V in W containing f(x), there exist an tri pre open set U of X containing x such that f(U)⊂ V;
• pcl(f^-1(B)) ⊂f^-1(cl(B)) for every subset B of Y.
• f(pcl(A)) ⊂cl(f(A)) for every subset A of X.
•  

4.6 Theorem 19

If f : (X, P₁ , P₂ , P₃ )→ (Y, W₁ , W₂ , W₃ ) and g : (Y, W₁ , W₂ , W₃) →(Z,η₁ ,η₂ , η₃) be two tri semi continuous function then gof : (X, P₁ , P₂ , P₃ ) →(Z,η₁ , η₂, η₃) may not be tri semi continuous function.

4.7 Theorem 20

Every tri continuous function is tri semi continuous function.

4.8 Theorem 21

Let f^-1 : (X, P₁ , P₂ , P₃ )→ (Y, W₁ , W₂ , W₃ ) be bijective. Then the following conditions are equivalent:

(i) f is a tri semi open continuous function.
(ii) f is a tri semi closed continuous function and
(iii) f^-1 is a tri semi continuous function.

Proof: (i)→ (ii) Suppose B is a tri closed set in X. Then X-B is an tri open set in X. Now by (i) f(X-B) is a tri semi open set in Y. Now since f^-1 is bijective so f(X - B) = Y - f(B). Hence f(B) is a tri semi closed set in Y. Therefore f is a tri semi closed continuous function.

(ii) →(iii) Let f is an tri semi closed map and B be tri closed set of X. Since f^-1 is bijective so (f^-1)^{- 1} (B) which is an tri semi closed set in Y. Hence f^-1 is tri semi continuous function.
(iii)→ (i) Let A be a tri open set in X. Since f^-1 is a tri semi continuous function so (f^-1)^-1 (A) = f(A) is a tri semi open set in Y. Hence f is tri semi open continuous function.

4.9 Theorem 22

Let X and Y are two tri topological spaces. Then f : (X, P₁ , P₂ , P₃ ) →(Y, W₁ , W₂ , W₃ ) is tri semi continuous function if one of the  followings holds:

• f^-1(s int(B)) ⊆s int(f^-1(B)), for every tri open set B in Y.
• scl(f^-1(B)) ⊆ f^-1(scl(B)), for every tri open set B in Y.

Proof: Let B be any T open set in Y and if condition (i) is satisfied then f^-1(s int(B)) ⊆s int(f^-1 (B)).
We get f^-1(B)⊆sint(f^-1(B)). Therefore f^{- 1}(B)is a tri semi open set in X. Hence f is tri semi continuous function. Similarly we can prove condition (ii).

4.10 Theorem 23

A function f : (X, P₁ , P₂ , P₃) →(Y, W₁ , W₂ , W₃ ) is called tri semi open continuous function if and only if f(s int(A))⊆ s int (f (A)), for every tri open set A in X.
Proof: Suppose that f is a tri semi open continuous function.
Since s int(A) ⊆ A so f(s int(A)) ⊆ f(A).
By hypothesis f(s int(A)) is an tri semi open set and s int(f(A)) is the largest tri semi open set contained in f(A), so f(s int(A)) ⊆s int (f(A)).
Conversely, suppose A is a tri open set in X. So f(s int(A))⊆s int (f(A)).
Now since A = s int(A), so f(A) ⊆s int(A)). Therefore, f(A) is a tri semi open set in Y and f is a tri semi open continuous function.

4.11 Theorem 24

A function f : (X, P₁ , P₂ , P₃)→(Y, W₁ , W₂ , W₃ ) is called tri semi closed continuous function if and only if scl(f(A)) ⊆ f(scl(A)), for every tri closed set A in X.
Proof: Suppose that f is a tri semi closed continuous function. since A ⊆ scl(A), so f(A) ⊆f(scl(A)). By hypothesis, f (scl(A)) is a tri semi closed set and scl(f(A)) is smallest tri semi closed set containing f(A) so scl(f(A)) ⊆ f(scl(A)).
Conversely, suppose A is an tri closed set in X. So scl(f(A)) ⊆ f(scl(A)).
Since A = scl(A) so scl(f(A)) ⊆ f(A). Therefore f(A) is a tri semi closed set in Y and f is tri semi closed continuous function.

4.12 Theorem 25

Every tri semi continuous function is a tri continuous function.

The authors have studied a new form of semi open and pre open set in tri topological space. They also studied tri continuous function, tri semi continuous function and tri pre continuous function in tri topological space. It is established that composition of any two tri semi open sets and two pre open sets in tri topological space is again a tri semi open set and a tri pre open set respectively in tri topological space. In tri continuity, tri semi continuity and tri pre continuity, inverse image of every tri open set, tri semi open set and tri pre open set is again tri open set, tri semi open and tri pre open set respectively.