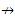bg*homeomorphism. Let, X= {a,b,c}, τ = {X,Φ , {a},{a,b}} and σ = {Y, Φ,{a},{b},{a,b}}. Define f: (X, τ)→(Y, σ) as f(a)=b, f(b)=a, f(c)=c. Then we observe that f is a g*b- homeomorphism but not bg*- homeomorphism.The aim of this paper is to define and develop a new type of homeomorphism called g*b-homeomorphism. Some of their properties and several characterizations of these types of functions with others are discussed in this paper. Some of the implications, relationships and independence relationships with few of the existing closed sets are studied and also, the author investigates the relationship between these classes of functions.
Many researchers have generalized the notion of homeomorphisms in topological spaces. Levine [8], [9] introduced the concept of generalized closed sets and strong continuity in topological space. Dunham and Levine [6] have studied some properties of generalized closed sets. Balachandran et al. [3] introduced the concept of generalized continuous function and proved that the class of generalized continuous function includes the class of continuous function and studied several properties related to it. Pushpalatha [14] introduced the concept of strongly generalized continuous function and studied several properties related to it. Pallaniappan and Rao [13] introduced the concept of regular generalized continuous function and proved that the class of regular generalized continuous function includes the class of continuous function and studied several properties related to it. Malghan [10] introduced the concept of generalized closed maps in topological spaces. Maki et al. [7] have introduced generalized homeomorphisms and gc homeomorphisms which are generalizations of homeomorphisms. Ahmad Al-Omari et al. [2] have generalized the concept of b-closed sets and obtained various topological properties. Crossley and Hildebrand [4] have introduced and studied semi- homeomorphisms which are strictly weaker than homeomorphisms in topological spaces. Every homeomorphism is a generalized homeomorphiosm but not vice-versa [5]. Generalized open maps, rg-closed maps, wg-closed maps and wg- open maps, w-open maps and wclosed maps, g*-open maps and g*-closed maps, pre-semi open maps, almost open maps, and α-open maps have been introduced and studied by Sundaram [17], Arockiarani [1], Nagaveni [12], Sheik Jhon [15], Crossely and Hildebrand [4], Singal and Singal [16], and Mashhour [11].
A subset A of a space X is said to be:
The complement of a b-open set is said to be b-closed. The intersection of all b-closed sets of X containing A is called the bclosure of A and is denoted by bCl(A). The union of all b-open sets of X contained in A is called b-interior of A and is denoted by bInt(A). The family of all b-open (resp. α-open, semi-open, pre-open,β-open, b-closed, pre-closed) subsets of a space X is denoted by bO(X) (resp. αO(X), SO(X), PO(X), βO(X), bC(X), PC (X)) and the collection of all b-open subsets of X containing a fixed point x is denoted by bO(X, x). The sets SO(X, x), αO(X, x), PO(X, x), βO(X, x) are defined analogously.
A subset of a topological space (X,τ) is said to be g*b-closed set in (X,τ) if bcl(A)⊆G whenever A⊆G where G is g-open. The collection of all g*b-closed sets of (X,τ) is denoted by G*bC (X,τ).
A subset of a topological space (X,τ) is said to be bg*-closed set in (X,τ) if bcl(A)⊆G whenever A⊆G where G is gb-open. The complement of g*b-closed (resp. bg*-closed) sets are called g*b-open (resp. bg*-open) Sets.
A bijection f: (X, τ)→(Y, σ) is called bg*- homeomorphism if f is both bg* -continuous and bg*-open.
A bijection f: (X, τ)→(Y, σ) is called gc-homeomorphism if f is both g- irresolute and its inverse f-1 is g- irresolute.
A bijection f: (X, τ)→(Y, σ) is called g*b- homeomorphism if f is both g*b-continuous and g*b-open.
A bijection f: (X, τ)→(Y, σ) is called g*cb- homeomorphism if f is both g*b- irresolute and its inverse f-1 is g*b-irresolute.
From the above definitions, we obtain the following remarks.
g*b-homeomorphism 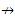bg*homeomorphism. Let, X= {a,b,c}, τ = {X,Φ , {a},{a,b}} and σ = {Y, Φ,{a},{b},{a,b}}. Define f: (X, τ)→(Y, σ) as f(a)=b, f(b)=a, f(c)=c. Then we observe that f is a g*b- homeomorphism but not bg*- homeomorphism.
g*b-homeomorphism 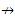g- homeomorphism.
Suppose that, X={a,b,c}, τ ={X, Φ, {b},{a,b}} and σ = {Y,Φ ,{b,c}}. Then the map f: (X, τ)→(Y, σ) defined by f(a)=a, f(b)=c, f(c)=b is g*b-homeomorphism but not g-homeomorphism
g*b-homeomorphism 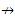g*cb- homeomorphism.
From the example 2, we notice that, f is g*b-homeomorphism. However, f is not g*cb-homeomorphism.
g*cb-homeomorphism 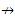gc-homeomorphism.
Let, X={a,b,c}, τ={X, Φ, {a},{b,c}} and σ = {Y, Φ, {a}}. Let f: (X, τ)→(Y, σ) be the identity map. Then f is a g*cb-homeomorphism but not gc-homeomorphism.
gc-homeomorphism 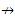g*cb- homeomorphism.
Consider, X={a,b,c}, τ={X,Φ , {b},{a,b}} and σ= {Y, , {a},{c},{a,c}}. Define f: (X, τ)→(Y, σ) as f(a)=a, f(b) =c, and f(c)=b. Then the map f is not a g*cb-homeomorphism, however f is a gc- homeomorphism.
g*b-homeomorphism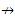 bg*c- homeomorphism.
Let X={a,b,c},τ ={X, Ф, {b},{a,b}} and σ = {X,Ф,{a},{a,c}}. If f: (X, τ)→(Y, σ) is the identity map, then f is g*b-homeomorphism but not a bg*c-homeomorphism.
bg*c-homeomorphism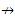 g*cb- homeomorphism.
From the example 2, we observe that f is a bg*c-homeomorphism but not a g*cb-homeomorphism.
g*cb-homeomorphism bg*c- homeomorphism.
Consider, X={a,b,c}, τ={ X,Φ , {b},{a,b}} and σ= {Y, , {a}}. Let f: (X, τ)→(Y, σ) be defined as f(a)=b, f(b)=a, f(c)=c. Then f is g*cb-homeomorphism but not a bg*c-homeomorphism.
The following example shows that the composition of two g*b- homeomorphism is not always a g*b-homeomorphism.
Let, X={a,b,c}, τ={X, Φ, {a},{a,b}} and σ = {Y, Φ,{a},{b},{a,b}} and η = {Z,Φ ,{b},{a,b}}. Define f: (X, τ)→(Y, σ) as f(a)=b, f(b)=a, f(c)=c and g: (Y,σ )→(Z, η) as g(a)=a , g(b)= c, g(c)=b. Here, we note that f and g are g*b-homeomorphisms. However g.f(X,τ ) →(Z, η) is not a g*b-homeomorphism.
Figure 1 shows the diagram of implications, which is obtained from the above definitions and from the remarks and the examples.
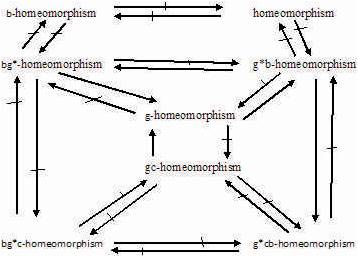
Figure 1. Implications of Definitions and Remarks
We shall categorize g*b-homeomorphism and g*b-open maps.
For any bijection f: (X, τ)→(Y, σ) the following statements are equivalent:
In this study, a new class of homeomorphism g*b homeomorphism is defined and many of their properties are characterized. Some of the implications, relationships and independence relationships with few of the existing closed sets are studied. It is found that all these functions are generalized g- continuous, open, closed, continuous functions and homeomorphisms respectively.
It is recommended that one can extend the study of g*b continuous functions and its basic properties in bitopological spaces, fuzzy topological spaces and intuitionistic fuzzy topological spaces, ideal topological spaces, grill topological paces and in minimal structures. This research work can be carried out further on studying properties of g*b compact space and g*b -connected space in various topological paces. There is a possibility of studying g*b functions in digital space, digital line and fuzzy topological spaces. In addition to above, one can investigate the above said notions various topological spaces.