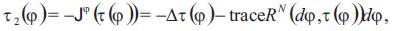
In this paper, the authors study Smarandache TN curves of general helices in the Sol³. Moreover, they characterize Smarandache TN curves of general helices in terms of their curvature and torsion. Finally, they found that the explicit parametric equations.

Mathematics Subject Classifications: 53A04, 53A10.

The Euler- Lagrange equation corresponding to E₂ is given by the vanishing of the bitension field

(1)

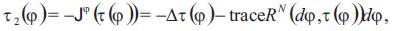
where J^φ is the Jacobi operator of φ. The equation τ₂(f) = 0 is called the biharmonic equation [1]. Since J^φ is linear, any harmonic map is biharmonic. Therefore, the authors are interested in proper biharmonic maps, that is non-harmonic biharmonic maps.

In this paper, they study Smarandache TN curves of general helices in the Sol³. They characterize Smarandache TN curves of general helices in terms of their curvature and torsion. Finally, found that the explicit parametric equations.

Sol space, one of Thurston's eight 3-dimensional geometries, can be viewed as R³ provided with Riemannian metric

(2)

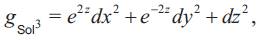
where (x, y, z) are the standard coordinates in R³.

Note that the Sol metric can also be written as:

(3)

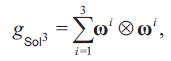
where

(4)

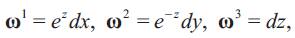
and the orthonormal basis dual to the 1-forms is

(5)

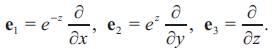
Proposition 2.1. For the covariant derivatives of the Levi-Civita connection of the left-invariant metric g_Sol³, defined above the following is true:

(6)

where the (i, j )-element in the table above equals 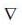_ei e_j for our basis

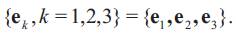
Lie brackets can be easily computed as:

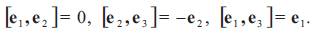
The isometry group of Sol³ has dimension 3. The connected component of the identity is generated by the following three families of isometries:

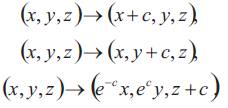
Assume that {T, N, B} be the Frenet frame field along γ [3]. Then, the Frenet frame satisfies the following Frenet--Serret equations:

(7)

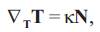
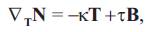
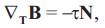
where κ is the curvature of γ and τ its torsion and

(8)

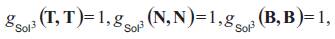
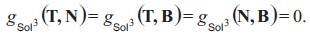
With respect to the orthonormal basis {e₁, e₂, e₃}, we can write

(9)

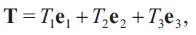
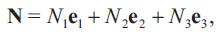
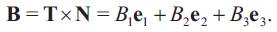
Theorem 3.1. ([2]) Let γ : I → Sol³ be a unit speed non-geodesic general helix. Then, the parametric equations of γ are

(10)

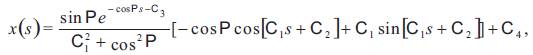
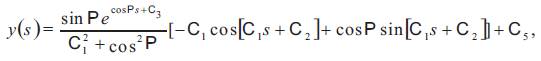
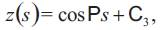
where C₁, C₂, C₃, C₄, C₅, are constants of integration

The obtained parametric equations for Eq.(10) is illustrated in Figure 1.

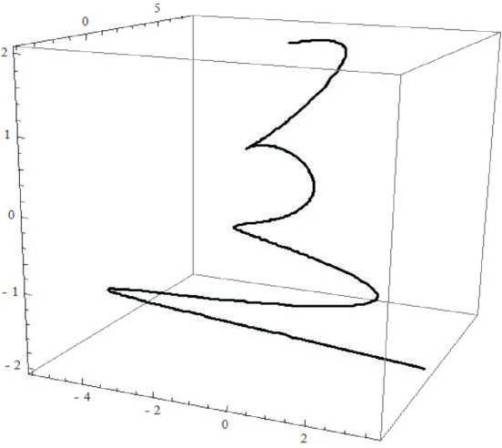
Figure 1. A unit speed non-geodesic general helix

Definition 4.1. Let γ : I → Sol³ be a unit speed B - slant helix in the Sol Space Sol³ and {T, N, B} be its moving Frenet frame. Smarandache TN curves are defined by

(11)

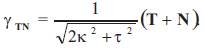
Theorem 4.2. Let γ : I → Sol³ be a unit speed non-geodesic general helix in the Sol Space Sol³. Then, the equation of Smarandache TN curves of a unit speed non-geodesic general helix is given by

(12)

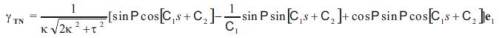
here C₁, C₂ are constants of integration.

Proof. Assume that γ be a unit speed non-geodesic general helix.

Using Theorem 3.2, we get

(13)

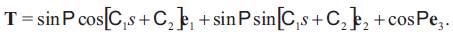
Using first equation of Eq.(3.3), we have

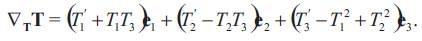
This can be rewritten as

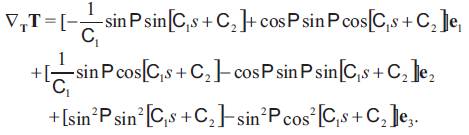
By the use of Frenet formulas and above equation, we get

(14)

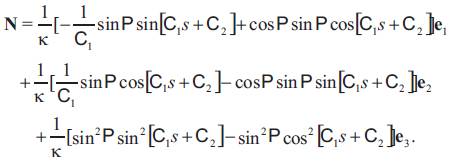
Substituting (13) and (14) in (11) we have (12), which completes the proof.

In terms of Eqs. (2) and (12), we may give:

Corollary 4.3. Let γ : I → Sol³ be a unit speed non-geodesic general helix in the Sol Space Sol³. Then, the parametric equations of Smarandache TN curves of a unit speed non-geodesic general helix are given by (Figure 2).

(15)

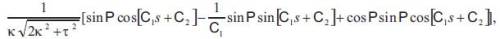
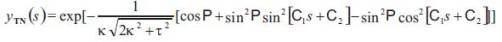
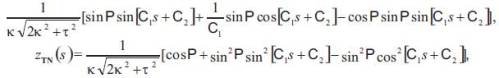
where C₁, C₂ are constants of integration.

Proof. Substituting (2) to (12), we have (15) as desired.

We may use Mathematica in Corollary 4.3, yields

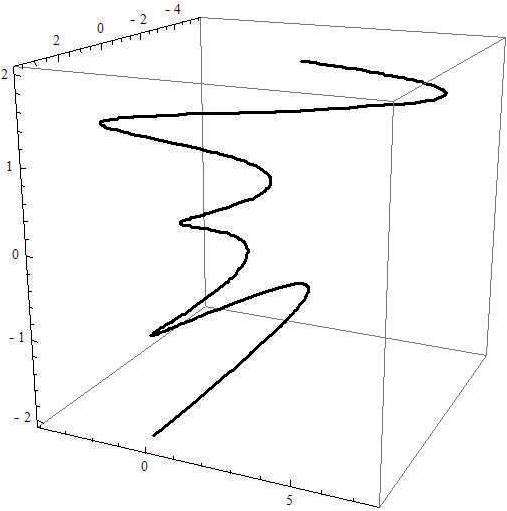
Figure 2. Smarandache TN curves of a unit speed non-geodesic general helix