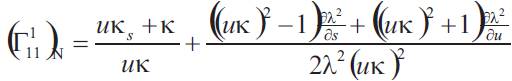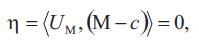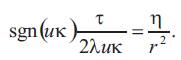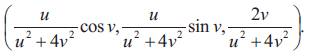The Inverse Surfaces Of Tangent Developables
With Respect To Sc (r)
Abstract
In this paper, the authors define the inverse surface of a tangent developable surface with respect to the sphere 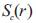 with
the center
with
the center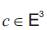 and the radius r in 3-dimensional Euclidean space
and the radius r in 3-dimensional Euclidean space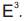 We obtain the curvatures, the Christoffel symbols
and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give
some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
We obtain the curvatures, the Christoffel symbols
and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give
some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
Msc. 11A25, 53A04, 53A05.
Keywords :
- Inversion,
- Inverse Surface,
- Developable Surface
- Fundamental forms,
- Christoffel Symbols.
1. Introduction
The last ten years, the developable ruled surfaces are studied by many mathematicians. Developable surfaces are a type
of important and fundamental surfaces universally used in industry design. Different methods have been presented for the
design of developable surfaces. The use of developable surfaces in ship design is of engineering importance because they
can be easily manufactured without stretching or tearing, or without the use of heat treatment. In some cases, a ship hull can
be entirely designed with the use of developable surfaces. See, [4,8,9,10,11].
On the other hand, a conformal map is a function which preserves the angles. The conformal mapping is an important
technique used in complex analysis and has many applications in different physical situations.
An inversion with respect to the sphere with the center
with the center  and the radius r given by
and the radius r given by
 is a conformal mapping and also is differentiable. In
is a conformal mapping and also is differentiable. In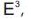 the inversion is a transformation defining between open
subsets of
the inversion is a transformation defining between open
subsets of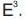
This paper is organised as follows: The authors firstly tell inversions and inversions of surfaces in . Secondly, they give the
fundamental forms, the curvatures(Gauss and mean), the shape operator and the Christoffel symbols of the tangent
developable surface. Finally, using by these properties, we obtain these of the inverse surface of the tangent developable surface.
. Secondly, they give the
fundamental forms, the curvatures(Gauss and mean), the shape operator and the Christoffel symbols of the tangent
developable surface. Finally, using by these properties, we obtain these of the inverse surface of the tangent developable surface.
2. Basic notions of inverse surfaces
Let and
and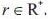 We denote that
We denote that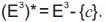 . Then, an inversion of
. Then, an inversion of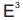 with the center
with the center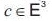 and the radius r is the map
and the radius r is the map
given by
Definition 2.1. [7] Let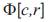 be an inversion with the center c and the radius r then, the tangent map of Ф at
be an inversion with the center c and the radius r then, the tangent map of Ф at is the
map
is the
map
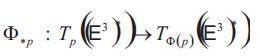
given by
where 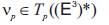
Now, let us assume that 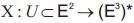 is the patch of a surface. The inverse patch of X with respect to
is the patch of a surface. The inverse patch of X with respect to  is the patch
given by
is the patch
given by
Throughout this paper, the authors assume that Φ is an inversion of with the center c and the radius r, X is a patch in
with the center c and the radius r, X is a patch in
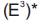 and Y is inverse patch of X with respect to Φ.
and Y is inverse patch of X with respect to Φ.
Let Ix , IIx and Kx , Hx be the first and second fundamental forms and the curvatures (Gauss and mean) of X, and let Iy , IIy , and Ky , Hy be these of Y, respectively. From[1], we have
where
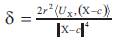 and
and 
3. The tangent developable surface
Let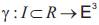 be a curve with arc-length s and {T,N,B} be Frenet frame along γ. Denote by κ and τ the curvature and the
torsion of the curve γ, respectively. Then we have Frenet formulas
be a curve with arc-length s and {T,N,B} be Frenet frame along γ. Denote by κ and τ the curvature and the
torsion of the curve γ, respectively. Then we have Frenet formulas
The tangent developable of γ is a ruled surface parametrized by
where T is unit tangent vector field of γ. As it is known, the coefficients of the first and second fundamental forms of the
surface M(s,u) have following
and
The normal vector field of the surface M(s,u) is given by
Next the curvatures (mean and Gaussian) and the matrix of shape operator of this surface are respectively as follows
and
Finally, the Christoffel symbols of the surface M(s,u) are given by
where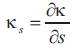
4. The inverse surface of the tangent developable
The authors show that N is the inverse surface of the tangent developable surface M with respect to the inversion Ф. Thus the
inverse surface N has following parametrization
Hence, if we take into account the equalities (2.3) and (2.4) then the coefficients of the first and second fundamental forms
of the inverse surface N by the help of these of the surface M are given by
where EN , FN , GN and eN, fN, gN are the coefficients of the first and second fundamental forms of the inverse surface respectively.
Morever, the Gauss and mean curvatures of the inverse surface N by the help of these of the surface M are respectively,
using by (2.5) and (2.6),
where KN and HN are the Gauss and the mean curvatures of the inverse surface N, respectively
Theorem 4.1. Let N be the inverse surface of the tangent developable surface M with respect to the inversion Ф. Denote by
SN the matrix of the shape operator of the inverse surface N, then SN is given by the help of that of M as follows
Proof. Let SM be the matrix of the shape operator of surface M. By using the equalities (2.3) and (2.4) we can write
where I2 is identity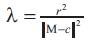 and
and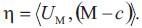 Hence from (3.6) and (4.7), we obtain that the equality (4.6) is satisfied.
Hence from (3.6) and (4.7), we obtain that the equality (4.6) is satisfied.
Theorem 4.2. Let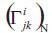 be the Christoffel symbols of the inverse surface N. The Christoffel symbols of the inverse surface N by
the help of these of the surface M are given by
be the Christoffel symbols of the inverse surface N. The Christoffel symbols of the inverse surface N by
the help of these of the surface M are given by
Proof. Considering the equality (2.3), for i, j , k = 1, we can write
where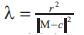 and
and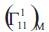 is the Christoffel symbol of the tangent developable surface. Thus, from the equalities (3.2) and (3.7), we obtain
is the Christoffel symbol of the tangent developable surface. Thus, from the equalities (3.2) and (3.7), we obtain
Others are found in similar way.
Theorem 4.3. Let N be the inverse surface of the tangent developable surface M with respect to the inversion Ф. Then the
inverse surface N is a flat surface if and only if either the normal lines to the surface M or the tangent planes of the surface M
pass through the center of inversion.
Proof. Let us assume that the inverse surface N is flat, then from (4.4), we can write
where either
or
If the equality (4.9) is satisfied, then the tangent planes of the surface M pass through the center of inversion. If the equality
(4.10) holds, then it follows
Namely, the normal lines to the surface M pass through the center of inversion.
The proof of sufficient condition is obvious.
Theorem 4.4. Let N be the inverse surface of the tangent developable surface M with respect Sc(r), to The inverse surface N is
minimal if and only if the normal lines to the surface M pass through the center of inversion (Figures 1 & 2)
Proof. The proof is same with that of Theorem 4.1.
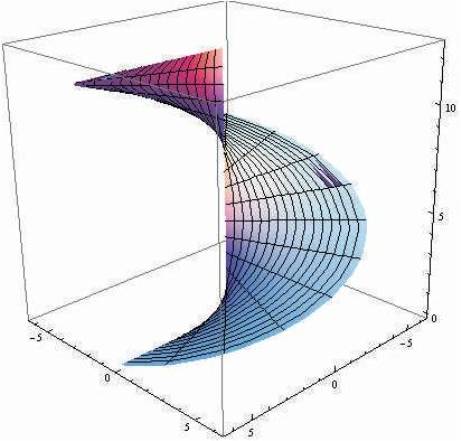
Figure 1. The helicoid given by (u cos v, u sin v, 2v)
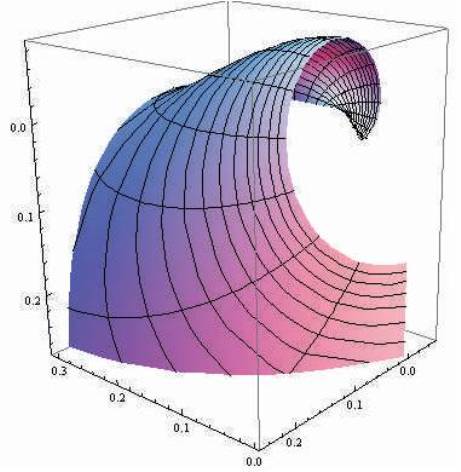
Figure 2. The inverse surface of the helicoid with respect to unit sphere given by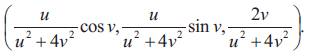
References
[1]. A. Gray: Modern differential geometry of curves and surfaces with mathematica. CRC Press LLC, 1998.
[2]. D. A. Brannan, M. F. Esplen, J. J. Gray : Geometry, Cambridge Universtiy Press, Cambridge, 1999.
[3]. D. E. Blair: Inversion theory and conformal mapping. American Mathematical Society, 2000.
[4]. E. Ozyilmaz, Y. Yayli: On the closed space-like developable ruled surface, Hadronic J. 23 (4) (2000) 439--456.
[5]. H. S. M. Coexeter: Inversive Geometry, Educational Studies in Mathematics, 3 (1971), 310-321.
[6]. F. Beardona, D. Mindap: Sphere-Preserving Maps in Inversive Geometry. Proceedings of the American Mathematical
Society, 130(4) (2001), 987-998.
[7]. PM. do Carmo : Riemann Geometry. Birkhauser, Boston, 1992.
[8]. P. Alegre, K. Arslan, A. Carriazo, C. Murathan and G. Öztürk: Some Special Types of Developable Ruled Surface,
Hacettepe Journal of Mathematics and Statistics, 39 (3) (2010), 319 -- 325.
[9]. S. Izumiya, H. Katsumi and T. Yamasaki: The rectifying developable and the spherical Darboux image of a space curve.
Geometry and topology of caustics-Caustics '98- Banach Center Publications, 50 (1999), 137-149.
[10]. S. Izumiya and N. Takeuchi: Special curves and ruled surfaces, Applicable Mathematics in the Golden Age (ed., J.C.
Misra), Narosa Publishing House, New Delhi, (2003) 305-338.
[11]-: New Special Curves and Developable Surfaces, Turk J Math 28 (2004), 153-163.
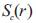 with
the center
with
the center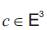 and the radius r in 3-dimensional Euclidean space
and the radius r in 3-dimensional Euclidean space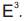 We obtain the curvatures, the Christoffel symbols
and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give
some necessary and sufficient conditions regarding the inverse surface being flat and minimal.
We obtain the curvatures, the Christoffel symbols
and the shape operator of this inverse surface by the help of these of the tangent developable surface. Morever, we give
some necessary and sufficient conditions regarding the inverse surface being flat and minimal. with the center
with the center  and the radius r given by
and the radius r given by
 is a conformal mapping and also is differentiable. In
is a conformal mapping and also is differentiable. In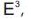 the inversion is a transformation defining between open
subsets of
the inversion is a transformation defining between open
subsets of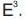
 . Secondly, they give the
fundamental forms, the curvatures(Gauss and mean), the shape operator and the Christoffel symbols of the tangent
developable surface. Finally, using by these properties, we obtain these of the inverse surface of the tangent developable surface.
. Secondly, they give the
fundamental forms, the curvatures(Gauss and mean), the shape operator and the Christoffel symbols of the tangent
developable surface. Finally, using by these properties, we obtain these of the inverse surface of the tangent developable surface. and
and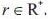 We denote that
We denote that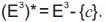 . Then, an inversion of
. Then, an inversion of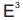 with the center
with the center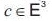 and the radius r is the map
and the radius r is the map
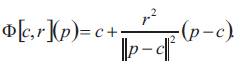
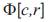 be an inversion with the center c and the radius r then, the tangent map of Ф at
be an inversion with the center c and the radius r then, the tangent map of Ф at is the
map
is the
map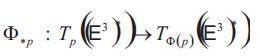
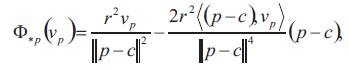
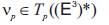
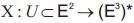 is the patch of a surface. The inverse patch of X with respect to
is the patch of a surface. The inverse patch of X with respect to  is the patch
given by
is the patch
given by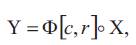
 with the center c and the radius r, X is a patch in
with the center c and the radius r, X is a patch in
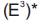 and Y is inverse patch of X with respect to Φ.
and Y is inverse patch of X with respect to Φ.
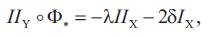

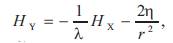

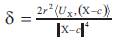 and
and 
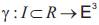 be a curve with arc-length s and {T,N,B} be Frenet frame along γ. Denote by κ and τ the curvature and the
torsion of the curve γ, respectively. Then we have Frenet formulas
be a curve with arc-length s and {T,N,B} be Frenet frame along γ. Denote by κ and τ the curvature and the
torsion of the curve γ, respectively. Then we have Frenet formulas
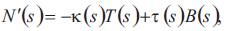
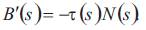

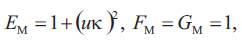
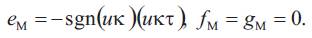

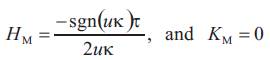

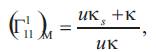

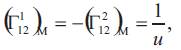

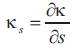
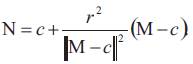
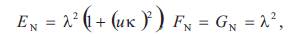
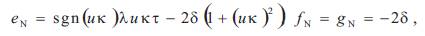
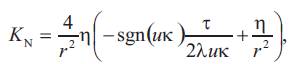


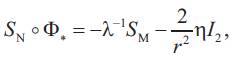
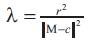 and
and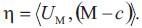 Hence from (3.6) and (4.7), we obtain that the equality (4.6) is satisfied.
Hence from (3.6) and (4.7), we obtain that the equality (4.6) is satisfied.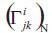 be the Christoffel symbols of the inverse surface N. The Christoffel symbols of the inverse surface N by
the help of these of the surface M are given by
be the Christoffel symbols of the inverse surface N. The Christoffel symbols of the inverse surface N by
the help of these of the surface M are given by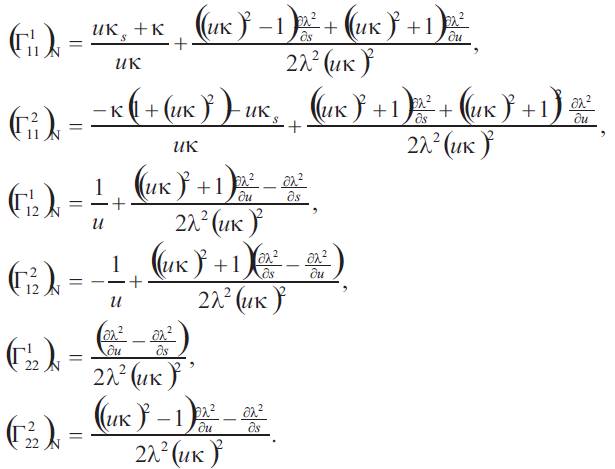

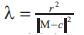 and
and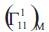 is the Christoffel symbol of the tangent developable surface. Thus, from the equalities (3.2) and (3.7), we obtain
is the Christoffel symbol of the tangent developable surface. Thus, from the equalities (3.2) and (3.7), we obtain