
This is the study of the grade-III fluid having the unidirectional and unsteady flow. Differential equation is solved using perturbation method to get linear forms of the velocities. The velocity u(y,t) is perturbed in ε to get the two-linear Partial Differential Equations (PDE's) in terms of u0(y,t) and u1(y,t). The solution of 1st linear is given in the exponent form f(y) eiat , that gives an ordinary differential equation that is easily solved to get the solution. This solution u0(y,t) is then utilized in Partial Differential Equation of 1st term velocity u1(y,t) and that gives linear Partial Differential Equation in the velocity u1(y,t). The solution of u1(y,t) is given in the exponent form F(y) e3iat , that gives an ordinary differential equation in F(y), that is solved to get the solution of F(y). This gives the perturbed solution for u1(y,t) in the form of F(y). First and zeroth solutions for the velocities give the solution for PDE.
Fluid Mechanics has the relevance in Engineering Mathematics that gives the properties of fluids. It performs an important part in science, engineering and technology. It is in the form of Newtonian and non-Newtonian fluids. The flow that gives the Newtonian fluid is the proportionality given by Newton’s Law of viscosity [1,2]. These are 3-dimensional, unsteady, nonlinear, Partial Differential Equations (PDE). The solution for these fluids is given by number of authors [1-6].
In these fluids, the viscosity and additional substantial factors are constant. These fluids have, in general, equations in higher order than the Newtonian equations. To overcome, we get the solution applying the perturbation method. Having this solution, the authors have given the velocity in terms of linear forms of equations. The zeroth boundary value problem is solved and its solution is substituted in first perturbation velocity. This solution is known exact perturbation solution [ 5, 7, 9, 13, and 14]. Other forms of solutions are given in the references [ 8, 10, 11, 12, 15, 16, and 17].
In this paper, the authors have given the unsteady partial differential equations for Newtonian (Viscous) and grade fluid having the slip conditions. The authors have given the solution in terms of perturbation with similarities [5, 6]. The perturbation equations are linear having zero and first velocities. The solutions of these perturbation solutions give the solution of PDE.
Grade III fluid has the form [6],

where,
p is pressure,
I is unit tensor,
µ is the co-efficient of viscosity,
α1 , α2 , β1, β2 and β3 are the material parameters and
A1 , A2 and A3 are the first three Rivlin-Ericksen [6, 11] tensors.
The tensors are given by,
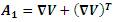
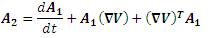
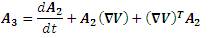
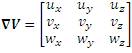
where,
V denotes the velocity vector
d/dt is the material time derivatives.
We are having the velocity of the form [4]
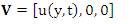
where,
u(y,t) is the velocity in x-direction.
Using equation (6) in equation (1) through equation (5) gives the following equation [3]

where
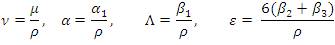
Equation (7) is the Partial Differential Equation (PDE) for unidirectional flow of grade-III fluid [6, 7, 8, 10, 11, 13].
We want to solve equation (7) with slip boundary condition. In the slip condition, the fluid is not having the same velocity as of its boundaries. This is given by:
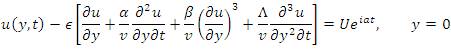
where as the other conditions are,
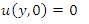
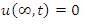
We use the perturbation in the velocity to get the linear forms of equation (7) and (8), then apply similarity to get the solution.
The solution of equation (7) is given in terms of perturbation in :

Using equation (11) similar powers of ε, we obtain the following equations at zeroth and first order respectively:
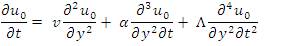
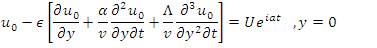
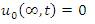
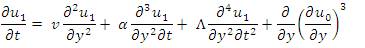
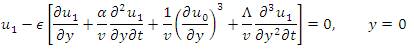
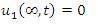
The solution of equation (12) subject to the boundary conditions (13) and (14), we have,
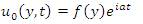
Using equation (18) in equations (12), (13) and (14), we have,
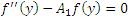
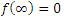
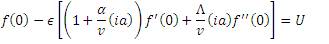
The solution of equation (19) subject to equations (20) and (21) is given in the form,
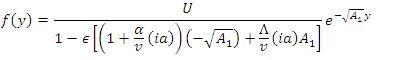
The unsteady velocity profile has the form
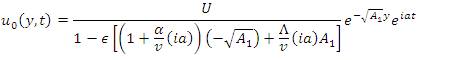
Differentiating equation (23) in equation (15) and equation (16), we get
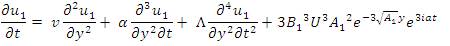
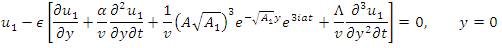
where,
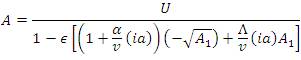
The solution of equation (24) subject to (25) and (17) is given as,
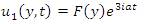
Using equation (26) in equation (24), equation (25) and equation (17), we have
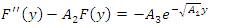
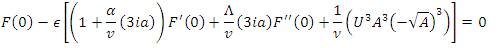

where,
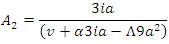
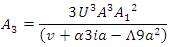
The solution of equation (27) subject to equation (28) and equation (29) is given by,

where,
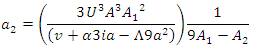
Therefore, unsteady velocity has form

The solutions given in equations (23) and (32) in equation (11), lead to
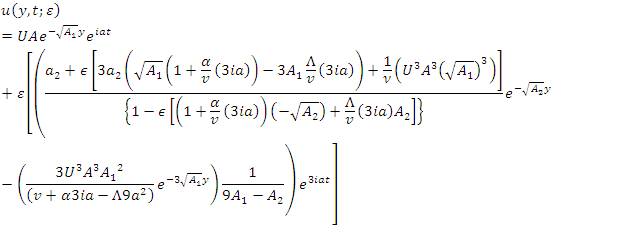
This is the unsteady solution for the velocity in 1-D fluid moving in the x-direction perpendicular to y-axis. The slip velocity at y=0 is given. Perturbation is the method of solution that makes the Partial Differential Equations a linear for the velocities. Therefore, we can get exact perturbation solution for u0(y,t) and u1(y,t) in terms of the factor .
The similarity transform is applied to differential equations having the form (12), (13) and (15), (16). These forms of equations (12), (13) and (15), (16) are linear after applying perturbation. This gives the benefit to have the solution of equations given in (7) and (8). Perturbation solutions given by (23) and (32) lead to the velocity (33) in and that gives the solution of (7).
The solution given in (23) and (32) gives the convergent (ε<1) solution for (33), that gives the satisfactory solution for the velocity (33).
The authors have given the solution of grade-III fluid having the slip condition. The flow is 1-D, uni-directional and unsteady. Solution of this fluid is given in perturbation:
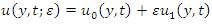
That has u0(y,t) as the zeroth solution and u1 (y,t) as the first order solution for the velocity in terms of ε.
At, y=0 the velocity of the fluid is of the form,
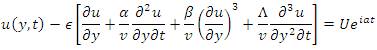
It has the contribution in the solutions of the velocity.
The similarity transforms,
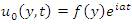

Gives the solution for f(y), F(y). The utilization of these gives the solution for unsteady velocity u0(y,t) and u1 (y,t).
Perturbation velocity having the similarity transform gives the solution for the velocity u(y,t).
Muhammad Raheel Mohyuddin is grateful to NCBAE, Gujrat, Pakistan for giving the respect as honorary Professor & Supervisor.