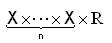( R, set of real numbers) is called a fuzzy anti n-norm on X if and only if:In this paper, the authors have studied some properties of contiunity and boundedness of linear mapping in fuzzy anti nnormed spaces. Firstly, the authors have given some definitions and theorem, such as fuzzy anti n-normed , fuzzy anti nnormed space and α - n - norms on fuzzy anti n-normed space, convergent sequence and Cauchy sequence on fuzzy anti n-normed space and fuzzy anti-n-Banach space, open ball and closed ball. The authors have presented some examples by using these definitions. Secondly, the authors have studied linear mapping on fuzzy anti n-normed spaces and the authors redefine fuzzy anti n-contiunity and fuzzy anti n-bounded by using previous definitions of continuity and boundedness. Additionally, the authors have given some definitions, weakly fuzzy anti n-continuous, strongly fuzzy anti ncontinuous, sequentially fuzzy anti n-continuous, using these definitions. Moreover, the authors have given the relationship between fuzzy anti n-continuity and fuzzy anti n- boundedness. Finally, the authors have showed that, T is strongly fuzzy anti n-continuous if and only if T is strongly fuzzy anti n-bounded and, T is weakly fuzzy anti n-continuous if and only if T is weakly fuzzy anti n-bounded.
Fuzzy norm theory was first introduced by Chang and Mordeson [1] and thereafter several authors contributed different articles on this concept and applied on different branches of pure and applied mathematics. Bag and Samanta [2] redefine fuzzy norm and fuzzy normed spaces.
Definition of Fuzzy anti norm was first introduced by Bag and Samanta [7]. Also Fuzzy anti 2-norm was indroduced by Reddy [3] and Fuzzy anti n-norm was introduced by Kavikumar, Jun and Khamis [4]. Following, Reddy [5] has defined Cauchy sequence and convergent sequence in fuzzy anti n-normed linear spaces and studied completeness of fuzzy anti n-normed linear spaces. Also some authors [8,9,10,11,12,13] studied some properties of fuzzy n-normed spaces and fuzzy anti n-normed spaces. Recently, Dinda, Samanta and Jebril [6], studied Fuzzy anti-bounded linear operator and some properties of this operator.
In this paper, the authors have studied some properties of contiunity and boundedness of linear mapping in fuzzy anti nnormed spaces. Firstly, the authors have given some definitions and theorem, such as fuzzy anti n-normed , fuzzy anti nnormed space and α - n - norms on fuzzy anti n-normed space, convergent sequence and Cauchy sequence on fuzzy anti n-normed space and fuzzy anti-n-Banach space, open ball and closed ball. The authors have presented some examples by using these definitions. Secondly, the authors have studied linear mapping on fuzzy anti n-normed spaces and the authors redefine fuzzy anti n-contiunity and fuzzy anti n-bounded by using previous definitions of contiunity and boundedness. Additionally, the authors have given some definitions, weakly fuzzy anti n-continuous, strongly fuzzy anti ncontinuous, sequentially fuzzy anti n-continuous, using these definitions. Moreover, the authors have given the relationship between fuzzy anti n-continuity and fuzzy anti n-boundedness. Finally, the authors have showed that T is strongly fuzzy anti ncontinuous if and only if T is strongly fuzzy anti n-bounded and, T is weakly fuzzy anti n-continuous if and only if T is weakly fuzzy anti n-bounded.
Let X be a linear space over a real field R. A fuzzy subset N* of 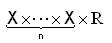( R, set of real numbers) is called a fuzzy anti n-norm on X if and only if:
(N*1) for all t ∈ R with t ≤ 0, N*(x1,x2 ....,xn,t) =1,
(N*2) for all t ∈ R with t > 0, N*(x1,x2 ....,xn,t) =0 if and only if x1,x2 ....,xn are linearly dependent,
(N*3) N*(x1,x2 ....,xn,t) is invariant under any permutation of x1,x2 ....,xn,
(N*4) for all t ∈ R with t> 0, N*(x1,x2 ....,cxn,t) =N (x1,x2....,cxn,t/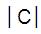
), if c ≠ 0, c ∈ R,
(N*5) for all s,t ∈ R
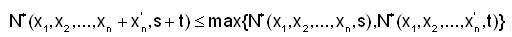
(N*6) N(x1,x2 ....,cxn,t) is a non- increasing function of R and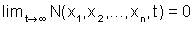
Then (X,N*) is called as a fuzzy anti n-normed linear space or in short f- an -Non Linear Space.
Let 
be a n-normed linear space. Define
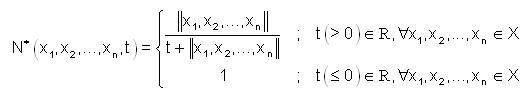
Then (X,N*) is a fuzzy anti n-normed linear space.
N* is a fuzzy anti n-norm on X if and only if (1-N*) is a fuzzy n-norm on X.
Let (X,N*) be a fuzzy anti n-normed space. Assume the condition that (N*7) N* (x1,x2 ....,xn,t)<1 for all t > 0 implies x1,x2 ....,xn are linearly dependent. Define 
. Then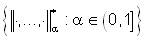 
is a descending family of n-norms on X. These n-norms are called α-n-norms on X corresponding to the fuzzy anti n-norm on X.
A sequence (Xk ) in a fuzzy anti n-normed linear space (X,N*) is said to be convergent to x ∈ X if given 0 < r < 1, t > 0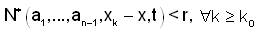
,
In a fuzzy anti n-normed linear space (X,N*), a sequence (X k) converges to x ∈ X if and only if,
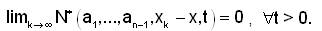
Let (X,N*) be a fuzzy anti-n-normed linear space. Let (Xk ) be a sequence in X then (Xk ) is said to be a Cauchy sequence if
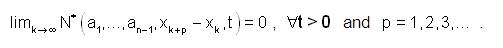
A fuzzy anti-n-normed linear space (X,N*) is said to be complete, if every Cauchy sequence is convergent in X. A complete fuzzy anti-n-normed space (X,N*) is called a fuzzy anti-n- Banach space.
The open ball B(t,r,x) and the closed ball B[t,r,x] with the center x ∈ X and radius 0 < r < 1, t > 0
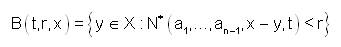
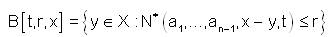
A subset A of X is said to be open if there exists r ∈ (0,1) such that,
B(t,r,x) ⊂ A for all x ∈ A and t>0. A subset A of X is said to be closed if for any sequence (xk ) in A converges to x ∈ A.
i.e.,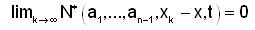 
for all t>0 implies that x ∈ A.
Let N* be a fuzzy anti-n-norm on X satisfying (N*7).
Define
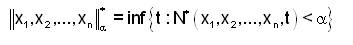
For each α ∈ (0,1] and x1,x2....,xn ∈ X. Then we have,
ii.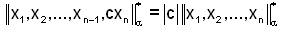 
for any scalar c.
iii.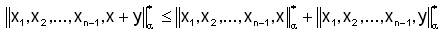 
for, x,y ∈ X
In this section, the authors have defined different types of continuity such as fuzzy anti n-continuity, sequential fuzzy anti ncontinuity, weakly fuzzy anti n-continuity, strongly fuzzy anti n-continuity of a mapping on fuzzy anti n-normed linear spaces. The notions of weakly fuzzy anti n-boundedness and strongly fuzzy anti n-boundedness are defined for linear mapping on fuzzy anti n-normed linear spaces. Then the relations between fuzzy anti n-continuity and fuzzy anti n-boundedness are studied.
Let X and Y be two linear spaces over the same field of scalars. Let N*1 and N*2 be two fuzzy anti n-norms on X and Y, respectively. Then, (X,N*1 ) and (Y,N*2 ) are fuzzy anti n-normed linear spaces.
T is mapping from X to Y. Then is said to be linear mapping on fuzzy anti n-normed spaces if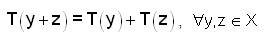
and T(cy)=c.T(y),c ∈ R.
A linear mapping T from X to Y is said to be fuzzy anti n-continuous at x0 ∈ X if for given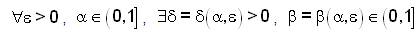 
such that for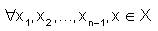 
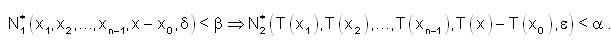
If T is fuzzy anti n-continuous at each point of X, then T is said to be fuzzy anti n-continuous on X.
A linear mapping T from X to Y is said to be strongly fuzzy anti n- continuous at x0 ∈ X, if for each ε>0,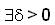 
such that 
,
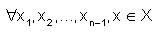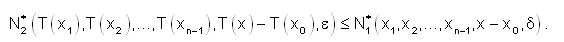
T is said to be strongly fuzzy anti n-continuous on X if T be strongly fuzzy continuous at each point on X.
A linear mapping T from X to Y is said to be strongly anti n- continuous at x0 ∈ X, if for a given ε>0,a∈(0,1],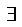 
δ=δ(α,ε)>0 such that ,
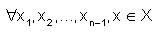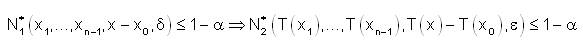
If T is weakly fuzzy anti n-continuous at each point of X, then we say that T is weakly fuzzy anti n-continuous on Xk,.
A linear mapping T from X to Y is said to be sequentially fuzzy anti n- continuous at x0 ∈ X , if for any sequence (Xk),
with Xk→X0 implies T(Xk)→T (X0).
ie, for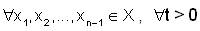 
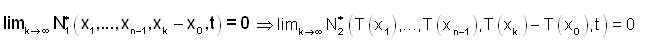
If T is sequentially fuzzy anti n-continuous at each point of X, then T is said to be sequentially fuzzy anti n-continuous on X.
If a mapping T from X to Y is strongly fuzzy anti n-continuous then it is weakly fuzzy anti n-continuous.
We suppose that, T is strongly fuzzy anti n-continuous at x0 ∈ X. Thus for each ε>0 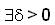such that for all X1,X2,....,Xn-1,x ∈ X
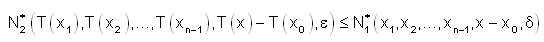
Let N*1 (x1,x2,....,xn- 1,x-x0,δ) ≤ 1- α where α ∈ (0,1]
Then,
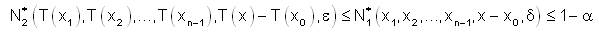
Therefore we get,
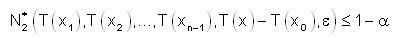
In this case, T is weakly fuzzy anti n-continuous.
If a mapping T from X to Y is strongly fuzzy anti n-continuous, then it is sequentially fuzzy anti n-continuous.
First we suppose that T, is strongly fuzzy anti n-continuous at x0 ∈ X.
Thus, for each ε>o,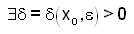 
such that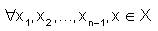
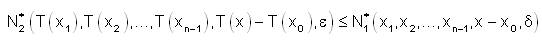
Let (xk ) be a sequence in X such that xk →x0,i.e,
Now from (i) we have,
By using (ii), we can get,
Since ε is a small arbitrary positive number, it follows that T(Xk)→T(X0).
Thus T is sequentially fuzzy anti n-continuous.
Let, T : X → Y be a linear mapping. Then T is fuzzy anti n- continuous, if it is sequentially fuzzy anti n-continuous.
Suppose T is fuzzy anti n-continuous at x0 ∈ X. Let (Xk ) be a sequence in X such that xk → x0.
Let ε>0 be given. Choose α ∈ (0,1]. Since T is fuzzy anti n-continuous at x0 , then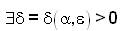
and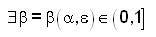 
such that for ,
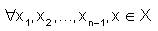Since, xk→ x0 in X,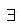
a positive integer k0 ∈ N such that,
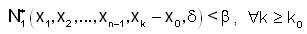
Then
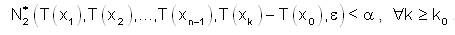
So for a given ε>0 and for any α ∈ (0,1], 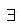a positive integer k0 such that,
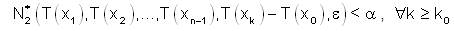
This implies,
Since ε>0 is arbitrary, thus T(Xk)→T (X0) in Y.
Thus T is sequentially fuzzy anti n-continuous.
Next we suppose that T is sequentially fuzzy anti n-continuous at x0 ∈ X.
If possible suppose that T is not fuzzy continuous at x0 .
Thus 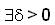and α ∈ (0,1] such that for any δ>0 and β∈ (0,1], 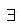w (depending on δ, β) such that for
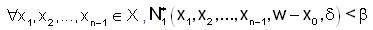
but
Thus for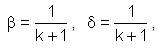
k=1,2,3......,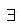Wk such that
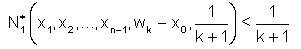
but
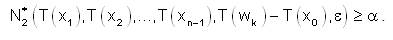
Taking δ>0,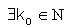
such that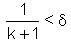 
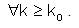
Then
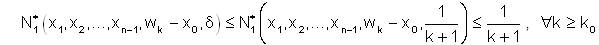
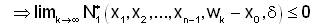
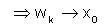
But from (13),
so,
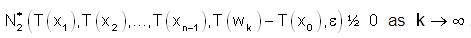
Thus T(wk) does not converge to T(x0) as wk → x0 (w.r.t N*1 ), which is a contradiction to their assumption.
Hence T is fuzzy anti n-continuous at x0 .
A linear mapping T from X to Y is said to be strongly fuzzy anti n- bounded on X if and only if there exist a positive real number M such that for all x1,x2,.....,xn-1,x ∈ X and for all s ∈ R,
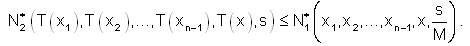
Example 1
The zero and identity mapping are strongly fuzzy anti n-bounded.
Example 2
This is an example of a strongly fuzzy anti n-bounded linear mapping other than the zero or identity mapping.
Let be a n-normed linear space. We define two functions N*1 and N*2 from Xx.....xXx R→(0,1] as,
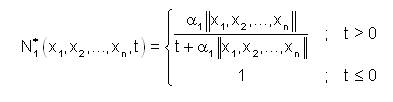
and
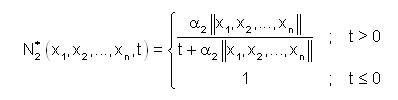
where, x1,x2,.....,xn ∈ X ,t∈ X, t ∈ R and α1, α2 are two fixed positive real numbers and α1> α2. Clearly, N*1 and N*2 are fuzzy anti n-norm on X. We now define a mapping T : (X,N*1 ) →(X,N*2 ) by T(x)=r.x, where, r∈R\{0} is fixed. Clearly T is a linear mapping. Choose an arbitrary but fixed M > 0 such that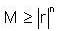 
and
x1,x2,.....,xn-1,x ∈ X. Now for t > 0,
i.e,
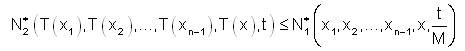
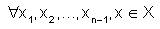and 
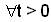
Now for t < 0,
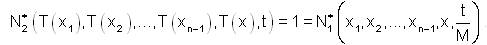
Hence, T is strongly fuzzy anti n-bounded on X.
A linear mapping T : X → Y is said to be weakly fuzzy anti n- bounded on X if and only if for any α∈(0,1] there exist Mα (>0) such that for all x1 ,x2 ,...,xn-1 ,x ∈ X and for all t ∈ R
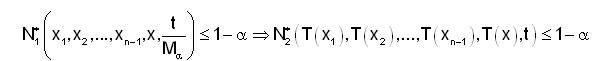
2.7.1 Theorem
Let T : X→ Y be a linear mapping. If T is strongly fuzzy anti n-bounded then it is weakly fuzzy anti n-bounded. But not conversely
Proof:
First we suppose that, T is strongly fuzzy anti n-bounded. Then there exist M > 0 such that for 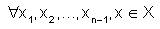and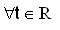
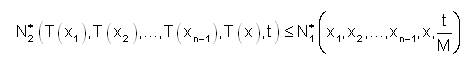
Thus for any a (0,1] there exists M (=M)>0 such that for 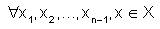and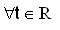
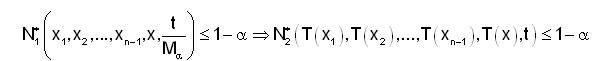
Hence T is weakly fuzzy anti n-bounded.
The converse of the above theorem is not necessarily true.
Example
Let be a linear space over the field R and N*1,N*2:Xx...xXx R→[0,1] be defined by,
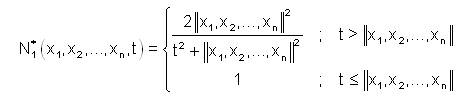
and
where, x1,x2,....,xn∈ X and t ∈R
Already we have seen that (X,N*1 ) and (X,N*2 ) fuzzy anti n-normed spaces.
Now we define a linear mapping T:X→X by T(X)=x,x ∈ X. Let α ∈ (0,1],x1,x2,...xn-1,x ∈ X and choose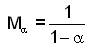 
We now prove that,
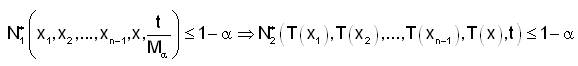
Then for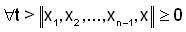
,
Now,
which is true for all α ∈ (0,1].
Hence,
Again, since for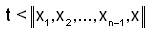 
it follows that,
Thus, T is weakly fuzzy anti n-bounded.
Now, we suppose that T is strongly fuzzy anti n-bounded.
Then there exist M(>0) ∈ R such that, for 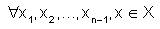and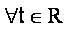 
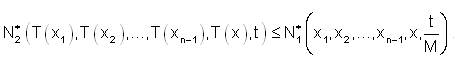
Now for
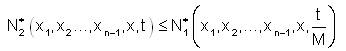
Hence, T is not strongly fuzzy anti n-bounded.
Let T : X→Y be a linear mapping. Then,
i. T is strongly fuzzy anti n-continuous on X if T is strongly fuzzy anti n-continuous at a point x0 ∈ X.
ii. T is strongly fuzzy anti n-continuous if and only if T is strongly fuzzy anti n-bounded.
Proof:
Since, T is strongly fuzzy anti n-continuous at x0 ∈ X, for each ε>0 there exists δ>0 such that for all x1,x2,....,xn-1,x ∈ X,
Taking x’ ∈ X and replacing x by x+x0-x’, we get,
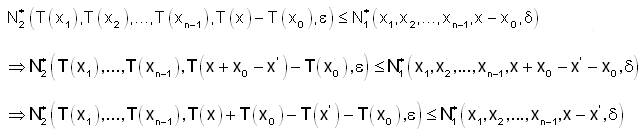
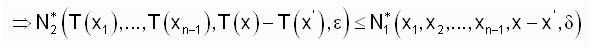
Since, x’ ∈ X is arbitrary, T is strongly fuzzy anti n- continuous on X.
First we suppose that T is strongly fuzzy anti-bounded. Thus there exist a positive real number M such that for all x1,...,xn-1 ,x ∈ X and for all t ∈ R+
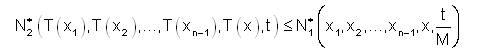
i.e.,
i.e.,
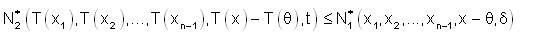
where 
Thus T is strongly fuzzy anti n-continuous at X and hence T is strongly fuzzy anti n-continuous on X.
Conversely, suppose that T is strongly fuzzy anti n-continuous on X. Using fuzzy anti n-continuity of T at x0 = θ ∈ X for ε=1 there exist δ >0 such that for all x1,...xn-1,x ∈ X
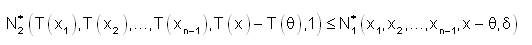
If x1,...xn-1,x are linear independent then T (x1),...,T(xn-1),T(x) are linear independent.
If x1,...xn-1,x are linear independent and t>0 then putting x=u.t
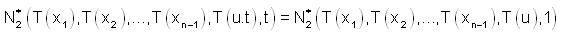
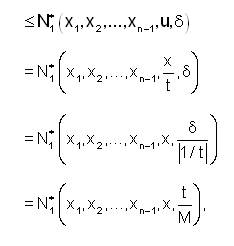
where,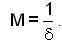 
So,
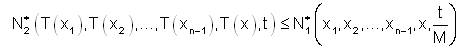
If x1,...xn-1,x are linear dependent then T (x1),...,T(xn-1 ),T(x) are linear dependent.
If x1,...xn-1,x are linear dependent and t>0 then,
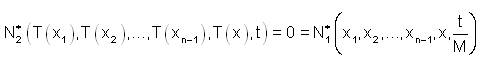
If x1,...xn-1,x∈X and t≤0 then,
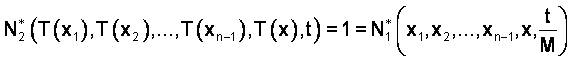
Hence T is strongly fuzzy anti n-bounded.
Remark
If T is strongly fuzzy anti n-bounded it is sequentially fuzzy anti n-continuous on X.
Let T:X→Y be a linear mapping. If T is sequentially fuzzy anti n-continious at x0∈X then it is sequentially fuzzy anti n-continious on X
Proof:
Let x∈X be an arbitrary point and let (xk) be a sequence in X such that xk →x. We suppose that T is fuzzy anti n-continuous at x0∈X.
Then, for all x1,...xn-1,x∈ X and , t>0
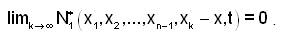
i.e,
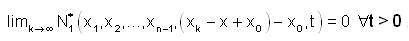
Since, T is fuzzy anti n-continuous at x0 we have,
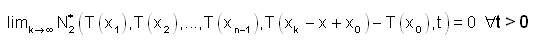
i.e.,
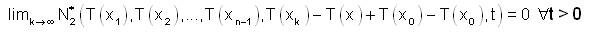
i.e.,
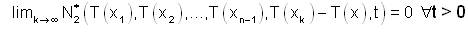
Thus, for all x1,x2,...xn-1,x∈X and 
This shows that T is sequentially fuzzy anti n-continuous on X.
2.7.4 Theorem
Let T : X→Y be a linear mapping. Then,
i. T is weakly fuzzy anti n-continuous on X, if T is weakly fuzzy anti n-continuous at a point x0∈ X.
ii. T is weakly fuzzy anti n-continuous if and only if T is weakly fuzzy anti n-bounded.
Proof:
Since, T is weakly fuzzy anti n-continuous at x0 ∈ X, for ε>0 and α ∈ (0,1] there exist δ=δ (α,ε)>0 such that for all x1,x2,....,xn-1,x ∈ X.
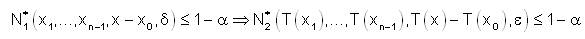
Taking x’ ∈ X and replacing x by x + x0 - x’ we get,
Since, x’∈ X is arbitrary it follows that T is weakly fuzzy anti n-continuous on X.
First, we suppose that T is fuzzy anti n-bounded. Thus, for any α ∈ (0,1] there exist Mα >0 such that 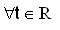and 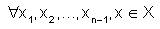we have,
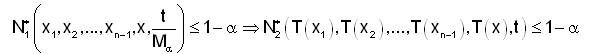
Therefore, for 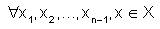and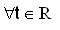
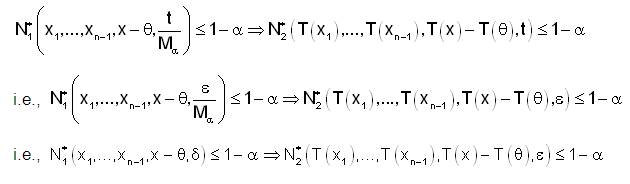
where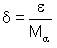 
Thus, T is weakly fuzzy anti n-continuous at θ∈X and hence weakly fuzzy anti n-continuous on X.
Conversely, suppose that T is weakly fuzzy anti n-continuous on X. Using continuity of T at θ ∈ X and taking ε=1 we have for all α∈(0,1] there exists δ= δ(α,1) >0 such that for all x1,x2,...,xn-1,x ∈ X,
If x1,...,xn-1,x are linear independent then T (x1),...,T(xn-1),T(x) are linear independent.
If x1,...,xn-1,x are linear independent and t>0 then putting x=u/t we have
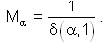
If x1,...,xn-1,x are linear dependent then T (x1),...,T(xn-1),T(x) are linear dependent.
If x1,...,xn-1,x are linear dependent and t>0 then
If x1,...,xn-1,x ∈ X and t ≤ 0 then
So, for all x1,...,xn-1,x ∈ X and t ∈ R,
Hence, T is weakly fuzzy anti n-bounded.
Finally, the authors have proved that their main theorem is as follows:
Let T : X → Y be a linear mapping. Then,
i. T is weakly fuzzy anti n-continuous on X if T is weakly fuzzy anti n-continuous at a point x0 ∈ X.
ii. T is weakly fuzzy anti n-continuous if and only if T is weakly fuzzy anti n-bounded.
Also, in this paper, the authors have studied some properties of continuity and boundedness of linear mapping in fuzzy anti nnormedspaces. First of all, the authors have defined different types of continuity such as fuzzy anti n-continuity, sequential fuzzy anti n-continuity, weakly fuzzy anti n-continuity, strongly fuzzy anti n-continuity of a mapping on fuzzy anti n-normed linear spaces. The notions of weakly fuzzy anti n-boundedness and strongly fuzzy anti n-boundedness are defined for linear mapping on fuzzy anti n-normed linear spaces. Then the relations between fuzzy anti n-continuity and fuzzy anti nboundedness are studied.
The authors will study some features of Convergence preserving linear mapping on fuzzy anti n-normed spaces in their future work.