The author states in a 2013, i-managers Journal on Educational Psychology article, “One of the most challenging areas of research in education involves the construction of specific instruments that are designed to measure qualitative outcomes and data” (Osler, 2013). This paper provides an in-depth discourse on the methodology used to create and aggregate data for the Tri–Squared Test to empower educators to develop digital qualitative metrics using an tenable model. The design and implementation of this type of research is quoted by the author in the aforementioned article, “Requires the research investigator to design an Instrument that ideally measures the variables under investigation” (Osler, 2013). This is the rationale for presenting the model outlined in detail in this paper. It clearly defines how to construct a Trichotomous research instrument to maximize efforts to acquire data regarding research questions and analyze the outcomes of those questions via the Tri–Squared Test.

The process of designing instruments for the purposes of assessment and evaluation is called Psychometrics. Psychometrics is broadly defined as the science of psychological assessment (Rust and Golombok, 1989). The Tri–Squared Test pioneered by the author; factors into the research design a unique event–based “Inventive Investigative Instrument”. This is the core of the Trichotomous-Squared Test. The entire procedure is grounded in the qualitative outcomes that are inputted as, “Trichotomous Categorical Variables based on the Inventive Investigative Instrument”, (Osler, 2012). The specific assessment of the variables is completely dependent upon the outcomes determined by the researcher's instrument. The creation production, and deployment of the trichotomous Inventive Investigative Instrument require that the research investigator adopt the role of a Trichotomous Psychometrician. A Trichotomous Psychometrician is an Educational Scientist, he uses trichotomous-based psychometric to develop a qualitative Inventive Investigative Instrument specifically designed to capture qualitative responses during a specific event (Osler, 2013).

The design of Inventive Investigative Instruments is based on the mathematical “Law of Trichotomy” (Apostol, 1967). Trichotomy itself is derived from historic discussions surrounding higher cognition, general thought, and descriptions of intellect. Philosopher Immanuel Kant (2007) adapted the Thomistic acts of intellect in his “Trichotomy of higher cognitio” - (a) understanding, (b) judgment, (c) reason - which he correlated with his adaptation in the soul's capacities - (a) cognitive faculties, (b) feeling of pleasure or displeasure, and (c) faculty of desire (Kant, 2007). It is important to note that in mathematics, the law (or axiom) of trichotomy is most commonly the statement that for any (real) numbers x and y, exactly th one of the following relations holds. Until, the end of the 19 century, the law of trichotomy was tacitly assumed true without having been thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. Mathematically, Trichotomous relations are irreflexive and anti- symmetric (Sensagent, 2012). A description of the entire Tri–Squared research process follows and is described in detail to provide the reader of the precise steps undertaken in the process of developing, designing, and ultimately implementing an Inventive Investigative Instrument (Osler, 2013). The model that immediately follow (Figure 1) provides an invariant (i.e. “unchanging”) mathematical tabular format for the construction of a Trichotomously Invariant Tri–Squared Inventive Instrument that maximizes the research outcomes for data analysis using the Tri–Squared Test (Osler, 2012).

Figure 1. The Inventive Investigative Instrument Metric that is Trichotomously Invariant [Unchanging]

The precise and careful tabulation of data is critical to the accuracy of the Tri–Squared Test. This why “Trichotometricians” (i.e., “Tri–Squared Researchers”) as Tri–Squared psychometric instrument developers (or “Tri–Squared Psychometricians”) are by nature and computation are very exact, detailed, and meticulous regarding the aggregation of data from the respective Inventive Investigative Instruments.

Tabulating data from Tri–Squared Inventive Investigative Instruments has the following parameters:

2.1 Trichotomous Categorical Variable One =a₁

It has the following data gathering structure per each individual instrument. The aggregation of all three Trichotomous categorical variables for this particular categorical variable [a₁] yields a single b₁ , b₂ or b₃ outcome variable (based upon responses tabulated using the mathematical Law of Trichotomy and the Tri–Squared Invariant Instrument Computational Researcher Decision Rule).

2.2 Trichotomous Categorical Variable Two =a₂

It has the following data gathering structure per each individual instrument. The aggregation of all three Trichotomous categorical variables for this particular categorical variable [a₂ ] yields a single b₁ , b₂ or b₃ outcome variable (based upon responses tabulated using the mathematical Law of Trichotomy and the Tri–Squared Invariant Instrument Computational Researcher Decision Rule).

2.3 Trichotomous Categorical Variable Three =a₃

It has the following data gathering structure per each individual instrument. The aggregation of all three Trichotomous Categorical Variables for this particular categorical variable [a₃ ] yields a single b₁ , b₂ or b₃ outcome variable (based upon responses tabulated using the mathematical Law of Trichotomy and the Tri–Squared Invariant Instrument Computational Researcher Decision Rule). The Tri–Squared Data Tabulation Methodology (Figure 2) is drawn from the Tri–Squared Inventive Investigative Instrument.

Figure 2. The Tri–Squared Trifold Data Tabulation Methodology

The tabulation of the outcomes of the Tri–Squared Inventive Investigative Instruments has the final research report that is presented in the Standard 3 × 3 Tri–Squared Table Trichotomous Categorical and outcome variables that are comprehensive results of the tabulation of all [n_Tri ] Tri–Squared Research Inventive Investigative Instruments. The comprehensive definition of the Standard 3 × 3 Tri–Squared Table is shown in Figure 3.

Figure 3. The Comprehensive Definition of the Standard 3 × 3 Tri–Squared Table

The Data Aggregation of the individual Tri–Squared Research Designed Inventive Investigative Instruments that is comprehensively expressed in the Tri–Squared Standard 3 × 3 Table (Osler, 2013) (representing the Data Aggregation for all research instruments) is calculated according to the Tri–Squared Data Aggregation Mathematical Algorithm. The “Tri–Squared Data Aggregation Mathematical Algorithm” is also called the “Trichotomous Invariant Instrument Inequality Formula” and it provides a comprehensive tally of Trichotomous outcome variables per each Trichotomous categorical variable for each individual Inventive Investigative Instrument. The mathematics of this process for the Trichotomous Categorical Variable Inventive Investigative Instrument Data Aggregation a is calculated as follows: “The following is true for 1 the First Trichotomous Categorical Variable”—According to the mathematical “Law of Trichotomy” the following applies in regards to the Tri–Squared Standard 3 × 3 Table Column a₁ :

a₁ =b₁ if b₁ ≥ 1 and b₂ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₁ =b₁ if b₁ ≥ {1}and b₂ =Ø, and b₃ =Ø, this directly corresponds to;

a₁ =b₂ if b₂ ≥ 1 and b₁ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₁ =b₂ if b₂ ≥ {1}and b₁ =Ø, and b₃ =Ø, and this directly corresponds to;

a₁ =b₃ if b₃ ≥ 1 and b₁ =0, and b₂ =0; or is defined in terms of set theory as follows:

a₁ =b₃ if b₃ ≥ {1}and b₁ =Ø, and b₂ =Ø;

For Trichotomous Categorical Variable Inventive Investigative Instrument Data Aggregation a₂ :

“The following is true for the Second Trichotomous Categorical Variable”—According to the mathematical “Law of Trichotomy” the following applies in regards to the Tri–Squared Standard 3 × 3 Table Column a₂ :

a₂ =b₁ if b₁ ≥ 1 and b₂ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₂ =b₁ if b₁ ≥ {1}and b₂ =Ø, and b₃ =Ø, this directly corresponds to;

a₂ =b₂ if b₂ ≥ 1 and b₁ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₂ =b₂ if b₂ ≥ {1}and b₁ =Ø, and b₃ =Ø, and this directly corresponds to;

a₂ =b₃ if b₃ ≥ 1 and b₁ =0, and b₂ =0; or is defined in terms of set theory as follows:

a₂ =b₃ if b₃ ≥ {1}and b₁ =Ø, and b₂ =Ø;

For Trichotomous Categorical Variable Inventive Investigative Instrument Data Aggregation a₃ :

According to the mathematical “Law of Trichotomy” the following applies in regards to the Tri–Squared Standard 3 × 3 Table Column a₃ :

a₃ =b₁ if b₁ ≥ 1 and b₂ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₃ =b₁ if b₁ ≥ {1}and b₂ =Ø, and b₃ =Ø, this directly corresponds to;

a₃ =b₂ if b₂ ≥ 1 and b₁ =0, and b₃ =0; or is defined in terms of set theory as follows:

a₃ =b₂ if b₂ ≥ {1}and b₁ =Ø, and b₃ =Ø, and this directly corresponds to;

a₃=b₃ if b₃ ≥ 1 and b₁ =0, and b₂ =0; or is defined in terms of set theory as follows:

a₃ =b₃ if b₃ ≥ {1}and b₁ =Ø, and b₂ =Ø;

If the encoded data returns with any two or all three Trichotomous Input Variables =Trichotomous Outcome Variables [b₁ —b₃] highlighted as equal, then the research investigator must use the Tri–Squared Computational Researcher Decision Rule (or “RDR”). The RDR is based upon a “Dichotomy” within the “Trichotomy” that is determined if two or more Trichotomous Categorical Variables are “polar opposites” and therefore “cancel each other out”. The RDR leads to a “Final Outcome” expressed in the following mathematical terms: If a=b=c, and a and b are polar opposites, then a “cancels out” b written as, a=b, and c as the remainder is left as the final solution. This is also true, if b=c (with a left as the final solution) and a=c (with b left as the final solution). The Researcher Decision Rule is further defined, expressed, and mathematically applied in terms of the Tri–Squared Trichotomous Outcome Variables (per each individual Inventive Investigative Instrument) in the following series of sequential steps: If b₁ = 1, and b₂ = 1, and b₃ = 1 for any Trichotomous Outcome Variable; then conduct the Tri–Squared Computational Researcher Decision Rule (RDR), where, b₁ =b₂ =b₃ for any Trichotomous Categorical Variable: [a₁ –a₃], Trichotomous Outcome Variables: [b₁ –b₃] for a₁ ; [b₄ –b₆] for a₂ ; and [b₇ –b₉] for a₃ ; then the researcher must examine the Trichotomous Categorical Variables: [a₁ –a₃] and determine if the outcome is either [b₁] or [b₂] or [b₃] by following the Categorical Variable Investigative Judgment:

If [b₁] and [b₂] are polar opposites then [b₁ cancels out b₂] and a₁ =b₃ ;

If [b₂] and [b₃] are polar opposites then [b₂ cancels out b₃] and a₁ =b₁ ; and

If [b₁] and [b₃] are polar opposites then [b₁ cancels out b₃] and a₁ =b₂ .

If there are no polar opposites that exist in the Inventive Investigative Instrument Trichotomous Outcome Variables then the Researcher Decision Rule requires the research investigator to make an “informed decision” in terms of the outcome of that particular variable. The informed decision must take into account the primary Trichotomous Categorical Variable (regarding the equality of the three Outcome Variables) to determine the final conclusive output that will be reflected in research comprehensive Data Aggregation.

The mathematical sequence of calculations to determine the collective Data Aggregation of all Inventive Investigative Instruments associated with a research investigation is tabulated in the following manner: For all n_Tri = The Total Number of collected Instruments from research participants (this number should equal the Total Number of research participants). The Collection of all data from all instruments has the following sequential mathematical equations:

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

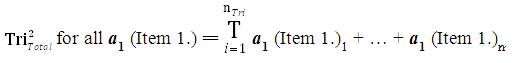
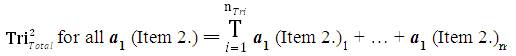
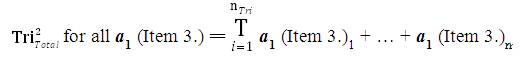
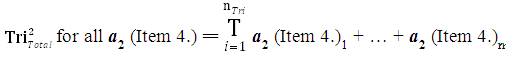
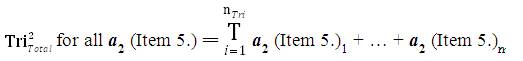
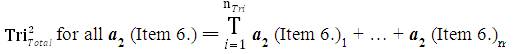
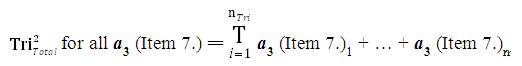
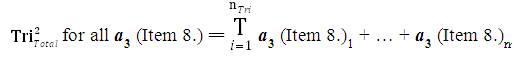
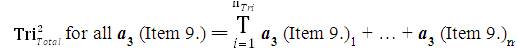
where,

T = Total

n_Tri = The Total Number of collected research Instruments

i = index (starting with the first collected instrument).

The use of the Trichotomously Invariant Inventive Investigative Instrument methodology greatly depends on the pre–determined research design. Due to the rigid and fixed nature of the Tri – Squared Test, the researcher must decide from the outset of the investigation whether or not the trichotomous model ideally fits the study. If there are overriding questions regarding multiple scales of measurement, lack of the value of trichotomous outcome, the necessity of a more qualitative (non–transformative) non–qualitative need for data or data verification then the Tri–Squared test and subsequent research methodology should not be used. If all of the aforementioned issues have been completely addressed and the implementation of the Tri–Squared model has value to the research design, then the Tri–Squared research model should proceed forward. The Tri–Squared research instrument is flexible in one area of its design (in terms of the qualitative questions) as long as the primary trichotomous instrument design is not violated. The Tri–Squared instrumentation is applicable to the following research tools and investigative inquiry methodologies:

a) Classroom observations;

b) Interviews (personal and through trichotomous survey–like questionnaires)

c) Documents (reports, articles, and publications); and

d) Observational analysis instrumental metrics.

The researcher makes the following dual recommendations regarding the implementation of Tri–Squared research Inventive Investigative Instruments:

• More research designs, investigations, and research studies need to be conducted using Tri–Squared research instruments (to broaden the breadth, depth, and use of trichotomous research);
• More collaborative trichotomous psychometric research designs are engaged in a variety of academic and non–academic disciplines (to increase the viability of trichotomous research outside of education in various arenas such as industry, health, etc.);
• As original trichotomous investigative measures (such as Trioinformatics (Osler, 2015)) and novel post hoc trichotomous statistical metrics (such as Triostatistics (Osler, 2014) such as TRINOVA (Osler, 2014); TRICOVA (Osler, 2015);Tri–Squared Meta–Analysis (Osler, 2015); Tri–Factor Analysis (Osler, 2015); TRICOM (Osler, 2015); MULTICOVA (Osler, 2015); Tri–Symmetrical Analytics (Osler, 2014); Trichotomous Progression Analysis (Osler, 2014); Trimetric Tri–Squared Test (Osler, 2014); and Tri–Center Analysis (Osler, 2014))are brought to light and additional research must be conducted to validate, verify, and make more viable Tri–Squared Test trichotomous research designs.

This monograph provided an in–depth discourse on psychometric models for the design and construction of digital instruments in the field of “Educational Science”. A research engineered computational instrument design model was provided that involved the Trifold assessment methodology. This methodology with its associated data aggregation models and corresponding metrics are used to conduct in–depth research investigations via the innovative Total Transformative Trichotomy–Squared [Tri–Squared] Test. The use of these models via subsequent research investigations and their ensuing outcomes can empower educators to design their own metrics. These metrics have qualitative and quantitative value having been derived through in–depth research investigations that have validated the use of the Tri–Squared investigative approach. The Tri–Squared Test provides research investigators with a novel set of tools that will aid them in the investigation of a variety of research areas such as: perceptions, case studies, affective domain dispositions, broad and general characterizations, assessment of creativity, self–reflective critiques, techniques used to measure appropriation, judgment and assessment of concepts, metacognitive assessment of ideology, and evaluation regarding prototypes and archetypes of novel instructional strategies, systems, and techniques. The completion of digital instrumentation (using the Tri–Squared research design as its foundation) will provide researchers with a means of creating innovative and inventive qualitative metrics that can be quantitatively analyzed. Such metrics enhance, supplement, and complement instruction and thereby provide additional value to teaching. This leads to constant improvement in the learning environment and has the ability to improve and broaden the research outlook and agenda of educational organizations and institutions. The creation of a model for the construction of digital instruments based on Tri–Squared calculations presents a new and innovative method of in–depth mixed methods investigation that delivers a detailed research design that has the potential to create virtual volumes of “Digital Trichotomous Psychometrics”. These Trichotomous Psychometrics can be used now and in the future to improve both educational curricula and infrastructures. In this manner, classrooms, instruction, learning, and education in general will continue improve and grow.