In the social sciences and life sciences, a case study (or case report) is a descriptive, exploratory or explanatory analysis of a person, group or event(Baxter and Jack, 2008) . Case Study research also called Single Subject research designs are an important part of social and behavioral sciences as they allow in–depth investigations into individual traits, perceptions, and perspectives. An explanatory case study is used to explore causation in order to find underlying principles (Dul and Hak, 2008). The Trichotomous Comparative Oneness of Measurement (represented by the acronym “TRICOM”) adapts the application of the Tri–Squared Test to carefully analyze single case study research. The application of the Tri–Squared Test into single subject designs increases the utility of the test, there by adjusting it into a highly adaptable statistic that can be used to efficiently and effectively investigate individual as well as large group research designs.

The construction of the Tri–Squared Statistic allows the individual investigations based upon the small sample size (in an interval of 1–16 extracted from the Tri–Squared series of Tables) in which an n of 1 has been factored into the Tri–Squared Test via the Tri–Squared distribution. The n of 1 allows the analysis of an single individual, however, Trichotomous Squared Comparative Oneness of Measurement explains the complete research methodology that should be used to most accurately analyze individual outcomes based upon a “Baseline” time line used for the delivery, collection, and analysis single subject data. TRICOM enables social behavioral scientists to investigate solitary subjects longitudinally to prospectively and retrospectively analyze specialized case study data.

Tri–Square or Tri–Squared comprehensively stands for “The Total Transformative Trichotomous–Squared Test” (or more simply “Trichotomy–Squared”). The Total Transformative Trichotomous–Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. It is based on the mathematical “Law of Trichotomy”. In terms of mathematics, Apostol in his book on calculus defined “The Law of Tricohotomy” as: Every real number is negative, 0, or positive. The law is sometimes stated as “For arbitrary real numbers “a” and “b”, exactly one of the relations:(1) a < b (2) a = b and (3) a > b, holds (Apostol, 1967).

The foundational idea of a “Trichotomy” has a detailed long history that is based on discussions surrounding higher cognition, general thought, and descriptions of intellect. Philosopher Immanuel Kant adapted the Thomistic acts of intellect in his trichotomy of higher cognition as: (a) Understanding;(b) Judgement; and (c) Reason. Using the aforementioned Kant correlated with his adaptation in the soul's capacities as: (a) Cognitive Faculties; (b) Feeling of Pleasure or Displeasure; and (c) Faculty of Desire (Kant, 2007) .

Using this trifold methodology, the Total Transformative Trichotomous–Squared Test provides a methodology for the transformation of the outcomes from qualitative research into measurable quantitative values that are used to test the validity of hypotheses. The advantage of this research procedure is that it is a comprehensive holistic testing methodology that is designed to be static way of holistically measuring categorical variables directly applicable to educational and social behavioral environments, where the established methods of pure experimental designs are easily violated. The unchanging base of the Tri–Squared Test is the 3 × 3 Table based on Trichotomous Categorical Variables and Trichotomous Outcome Variables. The emphasis the three distinctive variables provide a thorough rigorous robustness to the test that yields enough outcomes to determine if differences truly exist in the environment in which the research takes place(Osler, 2013a).

It is important to note that in mathematics, the law of trichotomy is most commonly the statement that for any (real) numbers  x and y, exactly one of the following relations holds. Until the end of the 19^th century the law of trichotomy was tacitly assumed true without thoroughly examined (Singh, 1997). A proof was sought by Logicians and the law was indeed proved to be true. If applied to cardinal numbers, the law of trichotomy is equivalent to the axiom of choice. More generally, a binary relation R on X is trichotomous if for all x and y in X, exactly one of xRy, yRx or x = y holds. If such a relation is also transitive it is a strict total order; this is a special case of a strict weak order. For example, in the case of three elements the relation R given by: (1) aRb; (2) aRc; and (3) bRc is a strict total order; While the relation “R” given by the cyclic “aRb, bRc, cRa is a “non–transitive trichotomous relation” (Sensagent, 2012).

In the definition of an ordered integral domain or ordered field, the law of trichotomy is usually taken as more foundational than the law of total order, with y = 0, where, 0 is the zero of the integral domain or field. In set theory, trichotomy is most commonly defined as a property that a binary relation “<” has when all its members satisfy exactly one of the relations listed above. Strict inequality is an example of a trichotomous relation in this sense. Trichotomous relations in this sense are irreflexive and antisymmetric(Sensagent, 2012).

The Tri–Squared Distribution is a static mathematical extraction out of the Chi Square distribution. This test is not the only test based on the Chi Square distribution (as it is a mathematical distribution that is frequently used directly or indirectly in many tests of significance). Similar to the Chi Square distribution, the Tri–Squared distribution has the following characteristics: (1) It has only a single parameter (the distribution Degrees of Freedom is written as “d.f.”); (2) The entire distribution is positively skewed; and (3) The Degrees of Freedom are mathematically written,“[C– 1][R–1]” which is equal to the distribution mean.

The Tri–Squared distribution has the following characteristics:

• The distribution Degrees of Freedom never changes;
• As a static test the “Tri–Squared Degrees of Freedom” is always [C– 1][R–1] =[3 – 1][3 –1] = [2][2] = 4 = the distribution mean;
• The distribution mode is always [d.f.– 2] = [4 – 2] = 2;
• The distribution median is always approximates [d.f. – 0.7] = [4 – 0.7] = 3.3;
• Due to the static or unchanging nature of the distribution, the distribution skew is always positive with the d.f. always equaling 4;
• The distribution formulae uses brackets “[ ]” in its formulaic notations to emphasize “a concentration on” (similar to the field of Chemistry) for purposes of clarity.

The Tri–Squared distribution is the foundation for the Tri–Squared Test which comprehensively incorporates the following Tri–Squared formulae: The Calculated Column Standard Deviation, The Calculated Row Standard Deviation, and The Sample Effect Size. The Tri–Squared Test is designed to create a comprehensive holistic research methodology from calculations conducted on the Standard 3 × 3 Tri–Squared Table which produces the following:

• A positive result;
• Noinformation on the variable relationship direction;
• Associated Effect Size, Sample Size, and Alpha Levels (Osler & Waden, 2012).

It is important to note that the research instrument used in Tri–Squared is an invariant (unchanging) fixed static Test

Tri–Squared is grounded in the combination of the application of the research of the two mathematical pioneers and the author's research in the basic two dimensional foundational approaches that ground further explorations into a three dimensional Instructional Design. The aforementioned research includes the original dissertation of optical pioneer Ernst Abbe who derived the distribution that would later become known as the chi square distribution and the original research of mathematician Auguste Bravais who pioneered the initial mathematical formula for correlation in his research on observational errors. The Tri–Squared research procedure uses an innovative series of mathematical formulae that do the following as a comprehensive whole:(1) Convert qualitative data into quantitative data; (2) Analyze inputted trichotomous qualitative outcomes; (3) Transform inputted trichotomous qualitative outcomes into outputted quantitative outcomes; and (4) Create a standalone distribution for the analysis possible outcomes and to establish an effective––research effect size and sample size with an associated alpha level to test the validity of an established research hypothesis.

The process of designing instruments for the purposes of assessment and evaluation is referred to as “Psychometrics”. Psychometrics is broadly defined as the science of psychological assessment(Rust & Golombok, 1989). The Tri–Squared Test pioneered by the author, factors into the research design a unique event–based “Inventive Investigative Instrument”. This is the core of the Trichotomous–Squared Test. The entire procedure is grounded in the qualitative outcomes that are inputted as Trichotomous Categorical Variables based on the Inventive Investigative Instrument (Osler, 2013). (Osler, 2012). defined the Tri–Squared mathematical formula in the Journal on Mathematics article entitled, “Trichotomy–Squared – A novel mixed methods test and research procedure designed to analyze, transform, and compare qualitative and quantitative data for education scientists who are administrators, practitioners, teachers, and technologists” as follows:

(1)

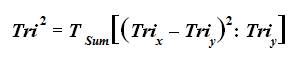
Trichotomous Comparative Oneness of Measurement takes the standard Trichotomous–Squared Test and applies it to functionally analyze a single case study. Thus, a TRICOM Test is a method used to conduct research on a single individual (n = 1). The power of the Test and its general applicability lies in the longitudinal repeated measurement of the researcher designed Trichotomous Inventive Investigative Instrument.

There are two forms of Repeated Measures in Trichotomously–Squared Inventive Investigative Instruments. They are: 1) Iterative repetitive Trifold Trichotomous Categorical Variables (a1, a2, anda3); and 2.) Nested Trifold Recursive Trichotomous Outcome Variables (b1, b2, and b3). “Iteration” is generally defined as the act of process repetition with the aim of reaching a desired target, goal, and/or result. Sequentially each subsequent “iterate”(individual iteration) is a repetition of the process. The outcome of an individual iteration is used as the starting point for the iteration that immediately follows. In the case of Tri–Squared research instruments, the term “Iteration” refers to breakdown of the overall overarching investigation research question into three specific Categorical Variables so that it can be accurately measured. The results of these variables will clearly statistically state whether or not the initial research question has merit. “Recursion” is broadly defined as the process of repeating items in a self–similar way. For example of this process consideran illustration that contains multiple or infinitesmaller and smaller nested identical images that repetitively occur over and over(as an identical image within an image within an image etc.). The term is applicable to the Tri–Squared researcher designed instrument in that it describes the three fold repetition of the structure of the Trichotomous Categorical Variable sub–questions that are each extracted from the three Categorical Variables (this thereby provides an Inventive Investigative Instrument that has a grand total of nine Trichotomous Outcomes nested within three interrelated but distinctively specific Trichotomous Categorical Variables the tabulated results of which create the Standard 3 × 3 Tri–Squared Table). The mathematical definition of Trichotomous Repeated Measures in terms of “Iteration” and “Recursion” is represented by the “Trichotomous Invariant Recursive Iterative Formula” in the following form:

(2)

Where, the following is true:

1) 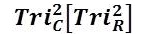= Trichotomous–Squared Columns (Categories);
2) 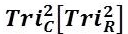= Nested Trichotomous–Squared Rows (Outcomes);
3) 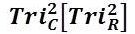 = Trichotomous Columns (Categories) with Nested Trichotomous Rows (Outcomes) within Trichotomous–Squared Columns.

The aforementioned formula literally means the following: “Trichotomous Outcome Variables in Rows are nested (contained) within Trichotomous Categorical Variable in Columns”. Repeated Measures Design is an internal characteristic of the Tri–Squared Test Inventive Investigative Instrument in terms of Trichotomous Outcome variables. The Tri–Squared Test instrument is constructed using the Inventive Investigative Instrument Metric that is Trichotomously Invariant [or “Unchanging”]. As a result of the Tri–Squared Repeated Measures Design, the Trichotomous Comparative Oneness of Measurement can be adapted to an investigative baseline timeline and the TRICOM Research Hypotheses can now be constructed.

Trichotomous Comparative Oneness of Measurement uses a set of sequential two–tailed hypothesis tests used to determine the significant difference of Tri–Squared Test Categorical and Outcome variables. TRICOM Hypothesis Tests have the following form:

H₀ :There is no significant difference in the Trichotomous Squared Comparative Oneness of Measurement interms of  Trichotomous Categorical and Outcome Variables indicating the results of longitudinal baseline testing designed to measure a given parameter.

H₁ :There is a significant difference in the Trichotomous Squared Comparative Oneness of Measurement in terms of  Trichotomous Categorical and Outcome Variables indicating the results of longitudinal baseline testing designed to measure a given parameter.

The TRICOM Mathematical Hypotheses:

(3)

(4)

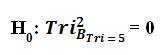
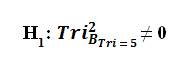
It is important to note that the TRICOM mathematical hypotheses reflect the repeated measures of the Tri–Squared Inventive Investigative Instrument via the Trichotomous Baseline Solution [Equation] (displayed above in the TRICOM Mathematical Hypotheses as BTri = 5).

The “TRICOM Baseline Tri–Squared Solution” has the following “TRICOM Baseline Tri–Squared Equation” mathematically defined in the following format:

B_Tri = Baseline Tri–Squared Solution[as an Equation]

(5)

(6)

(7)

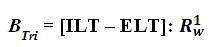
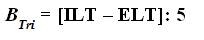
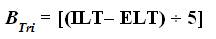
This equation is defined as, “Baseline Tri–Squared is equal to the concentrated Ideal Length of Time minus Expected Length of Time divided by the Conversion to One Research Work Week”. Where, the elements of the equation are as follows:

1) BTri= “Baseline Tri–Squared”, literally meaning “The total number of days allocated for the research investigation with one assessment day per research week assigned to disseminate, record, and collect the outcomes of the investigator's Inventive Investigative Instrument.”;
2) ILT = “Ideal Length of Time”, literally meaning “The researcher's ideal length of time needed to acquire the most idyllic research results.”;
3) ELT = “Expected Length of Time” = ILT • 0.5 = ILT/2, literally meaning “The time factored into the research design that take into account human and organizational social science parameters that can negatively affect the research results = ILT ÷ 2 or ILT/2= ILT/2.”;
4) R¹_W = “One Research Work Week” = “Research conducted during over a five day Work Week” = 5, literally meaning the  Total Number of Days Monday–Friday = 5;
5) 5 = [R¹_W ] = “Five Day Conversion Integer to One Research Work Week”, literally meaning The Total Number of Days for One  Research Work Week (Monday–Friday). Both the ILT and ELT are measured in terms of monthly days (with the average number of days in one month = 30 Days). ELT = ½ or 0.5 of ILT as illustrated in the Chart for ILT and ELT by Number of Days and Months as displayed below.

6.1 Summary of Table 1

Table 1 displays Chart One which exhibits the One Research Week = 5 days Monday through Friday, with Friday (the last day of the Research Week) as the target day of the Baseline (B_Tri) Behavior/Observation/Treatment Assessment (via the delivery of the researcher's Inventive Investigative Instrument). The mathematical formula is expressed in weeks in whole numbers and the “Triple I” is the repeated measure delivered at the end of each week (Friday). It is important to note the following: Baseline Tri–Squared [B_Tri] = Traditional Total Number of Tri–Squared Participants [n_Tri ], in TRICOM this is equal to the total number of  instruments collected throughout the established Baseline Timeline, thus, [B_Tri ] = [n_Tri ].

Table 1. Chart One for ILT [Ideal Length of Time] and ELT [Expected Length of Time]

6.2 An Example TRICOM Baseline Established Using Sample Data

Example TRICOM Repeated Measures using the Trichotomous Baseline Equation:

B_Tri = Baseline Tri–Squared Solution[B_Tri Equation]

(8)

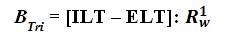
The researchers designs the investigation to take place over 3 Months = 90 Days for ILT. Thus, the following TRICOM research case study timeline is determined by calculating the following:

• ILT= “Ideal Length of Time” = 3 Months = 90 Days;
• ELT= “Expected Length of Time” = ILT • 0.5 = ILT/2 = 90/2 = 45 days;
• R¹_W= 5 = “Five Day Conversion Integer toOne Research Work Week”.

The Sample Data Example TRICOM Baseline  calculation is:

(9)

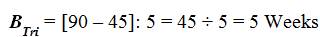
The TRICOM Case Study is n = 1 or [TCS_n=1 ] due to the Single Case Study with one individual as the research subject. The  investigation Baseline Tri–Squared [B_Tri ] was calculated to be = 9 weeks over a 3 Month period. Therefore, the Tri–Squared n  [n_Tri ] is determined from the Baseline Calculation to be 5 [n_Tri = 5 for TCS_n=1]. This indicates that over the 5 week research  period, 5 research instruments will be delivered to the single research participant. The instruments will also be collected and assessed over the 5 week research period. Thus, the Tri–Squared α level = 0.995 for n_Tri = 5 the Tri–Squared Calculated Value  is 0.207. Table 1 illustrates how the remainder of the TRICOM assessment data can now be calculated using the Tri–Squared Test. The complete workflow of a TRICOM calculation takes place in the next series of Tables. Table 1 illustrates the formulae and methodology used to calculate a TRICOM Test. Table 2 presents the actual TRICOM Test using sample data to determine a sample outcome.

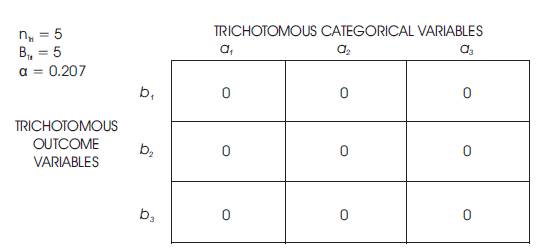
Table 2. A Sample Tri–Squared Test Structure for Calculating Trichotomous Squared Comparative Oneness of MeasurementOutcomes

Trichotomous Squared Comparative Oneness of MeasurementData Analysis Using the Standard Trichotomous–Squared Three by Three Table designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a₁ = Trichotomous Categorical Variable One; a₂ = Trichotomous Categorical Variable Two; and a₃ = Trichotomous Categorical Variable Three. The 3 × 3 Table has the following Trichotomous Outcome Variables:  b₁ = Trichotomous Outcome Variable One; b₂ = Trichotomous Outcome Variable Two; and b₃ = Trichotomous Outcome  Variable Three. The Inputted Qualitative Outcomes would be reported as follows:

The Tri–Square Test Formula for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to Determine the Validity of the Research Hypothesis:

(10)

(11)

6.3 Summary of Table 2

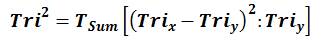
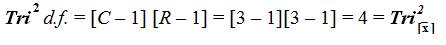
Table 2 illustrates the Standard 3 × 3 Table used to conduct a traditional Tri – squared Analysis that is the basic infrastructure of the TRICOM statistic. This Table is static and fixed always having nine cells and four degrees of freedom (d.f.) (thus, sampling to determine alpha level can be determined that ideally matches sample effect size). Table 3 follows Table 2 and illustrates an example TRICOM Test using a set of sample data.

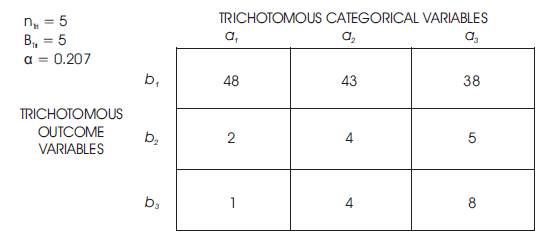
Table 3. Conducting an ExampleTRICOM Test with Sample Data

Trichotomous Squared Comparative Oneness of Measurement Data Analysis Using the Standard Trichotomous–Squared 3 × 3 Table designed to analyze the research questions from an Inventive Investigative Instrument with the following Trichotomous Categorical Variables: a₁ = Sample Data Successful via: sample Impact, and Positive Sample Testing [the  summation of the outcomes of the assessment instrument item 1]; a₂ = Made a Difference in Sample via: Sample  Participation, and Sample Graduation Rate [the summation of the outcomes of the assessment instrument item 2]; and a₃ =  Aided in Sample Retention via: Sample Drop Out Rate, and Sample Attendance [the summation of the outcomes of the assessment instrument item 3]. The 3 × 3 Table has the following Trichotomous Outcome Variables: b₁ = Yes; b₂ = No; and  b₃ = Unknown. The Inputted Qualitative Outcomes are reported as follows:

The Tri–Square Test Formula for the Transformation of Trichotomous Qualitative Outcomes into Trichotomous Quantitative Outcomes to Determine the Validity of the Research Hypothesis:

(12)

(13)

6.4 Summary of Table 3

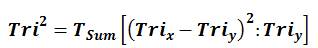
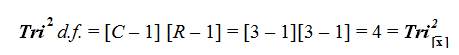
The calculated results of Table 3 are as follows:(1) Tri² Critical Value Table = 2.207 (with d.f. = 4 at α = 0.995); and (2) The Calculated Tri–Square Value is determined to be 8.131. The vast majority of data was in the first three cells of the Standard 3 × 3 Tri–Squared Table. The results of the Sample Data Tri–Squared Test follows and are covered in more detail in the section entitled “The Results of the Sample Data Tri–Squared Test”. The data provided carefully illustrates the results of the example TRICOM Test using the above set of sample data.

Table 2 illustrates the qualitative mathematical application of the Trichotomous–Squared (“Trichotomy–Squared”, “Tri–Squared” or “Tri–Square”) statistical analysis procedure. The results are:Tri² Calculated Value Table = 8.131 (with d.f. = 4 at α = 0.995). For d.f. = 4, the Critical Value for p > 0.995 is 0.207. The calculated Tri–Square value is 8.131, thus, the null hypothesis (H₀ ) is rejected by virtue of the hypothesis test which yields the following: Tri–Squared Critical Value of 0.207< 8.131  the Calculated Tri–Squared Value. The Table 1 3 × 3 Table reports the qualitative outcomes based on the Inventive Investigative Instrument Trichotomous Categorical Variables according to participant responses as the Trichotomous Outcome Variables. Table 1 shows that participants primarily and overwhelmingly selected the “Yes” Categorical Variable (a₁ b₁ = 48, a₂ b₁ = 43, and a₃ b₁ = 38) rather than the alternative Categorical Variables of either “No” or “Unknown” (the  “Unknown” C.V. indicated unselected or inapplicable responses to an item) (following the sample data extracted from Osler &Waden, 2012). The mathematical formula for the Tri–Squared is reported illustrating the final outcome of the research hypothesis test: the null hypothesis (H₀) is rejected at p > 0.995 is 0.207.

The Trichotomous Squared Comparative Oneness of Measurement Within Subjects [n = 1] for Tri–Squared Trend Series graphically displays research outcomes within Three Major Parameters of:

• Trichotomous Stability: which measures Trichotomous Categorical and Outcome Variable trends over measured research time =B_Tri on the 3 × 3 Tri–Squared Table and Variation Graphical Analysis (this is illustrated in Tables 1 and 2 respectively);
• Trichotomous Quantification: which measures Trichotomous Categorical and Outcome Variable amounts via the Standard 3 × 3 Tri–Squared Table and Slope Graphical Analysis illustration which effectively indicates the incline, decline or leveling out of measured Trichotomous Squared results; and
• Trichotomous Alteration: which measures Trichotomous Categorical and Outcome Variable changes in terms of the variability of observed Trichotomous perceptions, behaviors, or abilities due to participation in the research investigation displayed in the respective Variation Graphical Analysis (which reduces each variable into a relational plotted proportionate three coordinate chart) and Slope Graphical Analysis (which displays the aforementioned the incline, decline or leveling out of measured Trichotomous Squared results).

In terms of the research example, the Functional Analysis or Visual Data Analysis indicates that over the 5 week research period, 5 research instruments will be delivered to the single research participant. The instruments will also be collected and assessed over the 5 week research period. Thus, the Tri–Squared α level = 0.995 for n_Tri = 5 the Tri–Squared Calculated Value  is 0.207. The remainder of the TRICOM assessment data can now be calculated using the Tri–Squared Test as displayed in Figure 1.

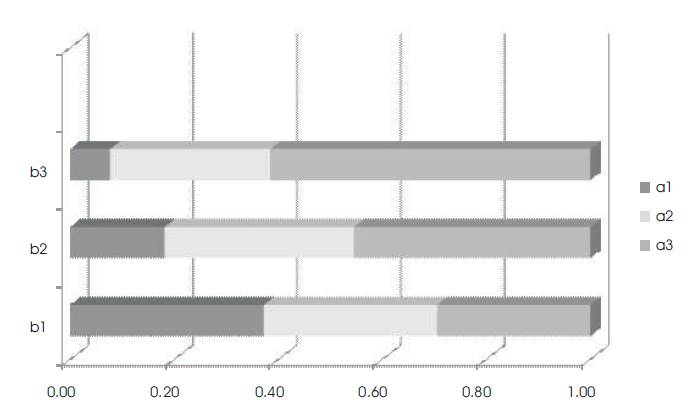
Figure 1. The Three Coordinate TRICOM Tri–Squared Variation Graphical Analysis of Sample Data

8.1 Summary of Figure 1

The Three Coordinate TRICOM Tri–Squared Graphical Analysis Chart is displayed above and converts the existing Tri–Squared sample data outcomes to proportions (that rest between the values of 0.00—1.00).Each bar the above Graphical Analysis Chart represents outcome values in terms of 100 percent = 1.00. The larger the size of the value (or in this particular case the Trichotomous Categorical or Outcome Variable) the greater the size of its shaded area (left to right or right to left). The Chart makes it easy to observe the relative size of Trichotomous Variables in terms of their relative proportionate sizes. Thus, the greatest value for the Trichotomous Categorical Variable values (a₁ —a₃ ) as noted in Figure 1 is a₁ . The greatest value for the  Trichotomous Outcome Variable values (b₁ —b₃ ) as noted in Figure 1 is b₁ . Thus, comparatively, the overall largest  Trichotomous Categorical and Outcome Variable value in the TRICOM Tri–Squared 3 × 3 Table cell a₁ b₁ = 0.48. The second in terms of Trichotomous Categorical and Outcome Variable values proportion sample data size is cell a₂ b₁ = 0.43 and the  third in proportionate size is cell a₃ b₁ = 0.38. Figure 2 exhibits the inclination of the Sample Data on a Slope Graphical  Analysis.

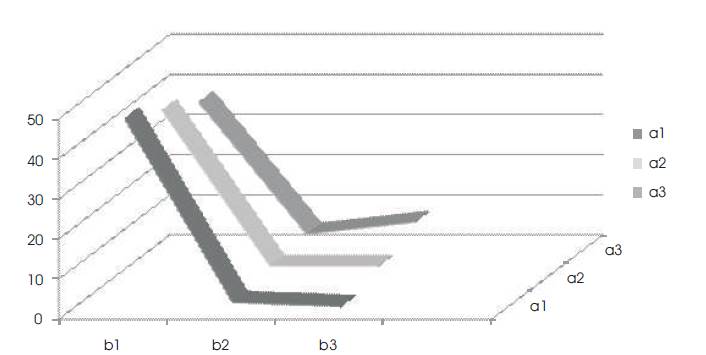
Figure 2. The Three Coordinate TRICOM Tri–Squared Slope Graphical Analysis of Sample Data

8.2 Summary of Figure 2

The Three Coordinate TRICOM Tri–Squared Slope Graphical Analysis Chart displaying the slope of Sample Data Tri–Squared outcomes on a Multi–Slope graph (between 0—50 due to the highest value ending at 48). The Trichotomous three value graphical slope analysis indicates that the maximum results are at the top of the slope (left hand side), the smallest values are at the base of the slope (middle arc of the slope), the middle values are at opposite end of the slope (right hand side). The Slope Graphical Analysis Chart indicates the greatest differential in terms of Trichotomous Alteration (displaying the incline, decline or leveling out of measured Trichotomous Squared results) was in the first column of the TRICOM Tri–Squared 3 × 3 Table. The first column of the TRICOM Tri–Squared 3 × 3 Table had the following data reported in its cells: 1) a₁ b₁ = 48; 2)  a₁ b₂ = 2; and 3) a₁ b₃ = 1. This was followed by the second column of the TRICOM Tri–Squared 3 × 3 Table that had the  following data reported in its cells: 1) a₂ b₁ = 43; 2) a₂ b₂ = 4; and 3) a₂ b₃ = 4. The final slope had the greatest slope in terms of  overall values in less than 10 (10 > TRICOM Tri–Squared Columns n_2...3 ) but the least overall incline in terms of the TRICOM  Tri–Squared 3 × 3 Table that had the following data reported in its cells: 1) a₃ b₁ = 38; 2) a₃ b₂ = 5; and 3) a₃ b₃ = 8.

H₀ : [Rejected] There is no significant difference in the Trichotomous Squared Comparative Oneness of Measurement in terms  of Trichotomous Categorical and Outcome Variables indicating the results of longitudinal baseline testing designed to measure a given parameter.

H₁ : [Accepted] There is a significant difference in the Trichotomous Squared Comparative Oneness of Measurement in terms  of Trichotomous Categorical and Outcome Variables indicating the results of longitudinal baseline testing designed to measure a given parameter.

9.1 Further TRICOM Mathematical Hypothesis Results:

(14)

(15)

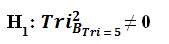
The following observations can be stated based on the results of the TRICOM Tri–Squared calculations and Visual Data Analysis: 1) The TRICOM Tri–Squared Test with n = 5 and an associated alpha level (α = 0.995) indicates that the sample Tri research is statistically significant at α Level = 0.995; 2) The TRICOM Tri–Squared Test rejected the null hypothesis and accepted the following alternative outcome: 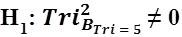. The visual analysis of the data yielded the following: a) The  greatest value for the Trichotomous Categorical Variable values (a₁ —a₃ ) was Categorical Value a₁ ; b) The greatest value for  the Trichotomous Outcome Variable values (b₁ —b₃ ) as noted in Figure 1 was b₁ ; c) Comparatively, the overall largest  Trichotomous Categorical and Outcome Variable value in the TRICOM Tri–Squared 3 × 3 Table cell a₁ b₁ = 0.48; d) Second in  terms of Trichotomous Categorical and Outcome Variable values proportion sample data size was cell a₂ b₁ = 0.43; e) The  third in proportionate size is cell a₃ b₁ = 0.38; and f) In terms of Trichotomous Slope the first column of the TRICOM Tri–Squared  3 × 3 Table had the following data reported in its respective cells = 1.) a₁ b₁ = 48; 2) a₁ b₂ = 2; and 3) a₁ b₃ = 1. This was by far  the largest sample data set in terms of Trichotomous incline, decline or leveling out of measured Trichotomous Squared results. Analysis of the sample data provided gives a clear indication that over the time period of 5 weeks the single case under observation clearly provided a vast differentiation in perspective regarding the given parameter.

The overall efficacy of these results is representative of the overall objectivity, reliability, utility, and validity of the TRICOM statistic. The results also indicate that the TRICOM Test is a very effective method for the analysis of single case studies (and for conducting single case study research). This innovative and novel statistic is a specialized form of the Tri–Squared Test designed to provide researchers with more fluidity and flexibility in their use of the Tri–Squaredresearch methodology. TRICOM both enables and empowers educational scientists and researchers to conduct in–depth individual–based research designs. The addition of this new statistic to the battery of Trichotomous Squared statistical metrics increases the overall functionality of the Trichotomous Squared Test from both an analytical and an investigative perspective.