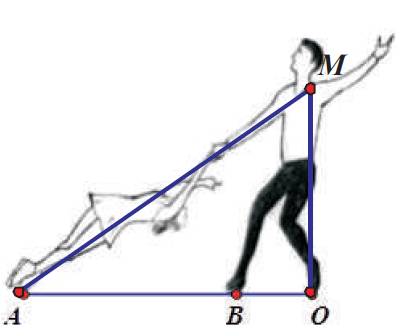
Figure 1. Illustration of the death spiral, side view
In light of the Winter Olympic Games, a mathematical modeling problem involving algebra and geometry is presented via dynamic geometry software in the context of pairsfigure skating. The death spiral involves a lady and man forming concentric circles with their blades on the ice. In-service elementary, middle and high school teachers used knowledge of rates and circumference to solve problems involving the death spiral. Teachers' work is analyzed and discussed.
As teachers are increasingly expected to align their curricula with the Common Core State Standards (CCSI, 2010), problem solving situations connecting science and mathematics can help teachers address the Model with Mathematics Standard for Mathematical Practice in their classrooms. Professional development can expose teachers to models, strengthen teachers' subject matter knowledge, and enhance teachers'specialized content knowledge.
Research in situated cognition has shown that middle school students learn better when they interact with contexts which they find motivating (Greeno 1993). In this article, we provide a modeling situation involving pairs figure skating, which can serve as a motivating context since many students are interested in sports contested in the Winter Olympic Games. Figure skating is one of the most attractive Winter Olympic sports to watch because it combines artistry and athleticism; in fact, figure skating is the most popular sport to watch among females aged 12 + in the country (US Figure Skating, 2013).
Seven in-service elementary, middle and high school teachers, whom we refer to as students in this article, took a graduate-level problem solving class during the summer 2013 semester at a public university and completed this activity during the course. We discuss students' explanations to problems that involve connecting geometry and algebra within the context of the death spiral, a required element in the pairs figure skating program. While completing this activity, students had access to computers and were familiar with Geometer's Sketchpad software, a software which provides a dynamic geometry environment.
The death spiral is a required element of a pair team's routine. In order to perform the death spiral, the man holds one of the lady's hands, as shown in Figure 1

Figure 1. Illustration of the death spiral, side view
The man pivots in a circle with one of his skates at a fixed point, denoted by point O, on the ice while the other skate, denoted by point B, is traveling around in a circle. Simultaneously, the lady moves around him in a circular path with only one of her blades, denoted by point A, touching the ice (Kerrigan & Spencer, 2003).The man's height MO decreases as the lady's torso slides horizontally such that OA increases. The lady's torso becomes low and almost parallel to the ice. When the man raises out of his pivot, the lady returns to an upright position. The success of this spiral depends on the cooperative work of both partners, since any minor error can make the death spiral collapse.
There are two, two-dimensional projections of the three-dimensional death spiral(see Figure 2). The first projection, the y-z projection, was explained above.
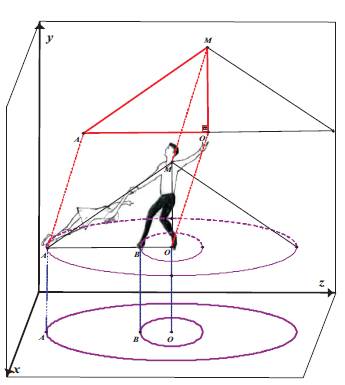
Figure 2. Two two-dimensional projections of three-dimensional death spiral
The second two-dimensional projection is the bird's eye view, or x-z projection, of the tracings which the man's and lady's blades form on the ice when they rotate a full revolution. This is the projection which is the focus of the activity in this article. The man, whose center of mass is above point O on the ice, pivots in a small circle on the ice with radius OB while the lady glides in a circle with an increasing radius around the man until she reaches her fully extended position with radius OA. While the tracings of the man's and lady's blades are in fact spirals, for the purposes of this activity, we treat the tracings of the blades as two concentric circles centered around point O, as shown in Figure 3.
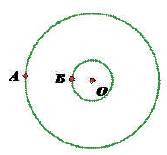
Figure 3. Concentric circles: Bird's eye view (x-z projection) of death spiral blade tracings
When we introduced the death spiral to the students, we showed them youtube clips of pairs teams performing the move so that they would get a sense of the dynamics of the death spiral as they happen in real time. The names of the pairs team of KeaunaMacLaughlin and Rockne Brubaker, 2007 World Junior Champions and 2008 and 2009 US National Champions, were used in the problem.
The problems which students were asked to solve are listed below:
1. Does Keauna or Rockne travel faster during the death spiral? Explain how you determined your answer. 2. If OA = 10 feet, and OB = 2 feet, answer the following questions:
a. In one revolution, how much further does Keauna travel than Rockne? Explain.
b. If the death spiral took 8 seconds to complete, what is the difference in speeds of Keauna and Rockne? Explain.
c. Your student Lisa is trying to answer previous two questions and she first calculates the difference between the lengths of OA and OB. Is this a valid first step to solve the above two questions? If so, how could she use it, and if not, explain why not.
In what follows, we discuss the mathematical goals of these two problems, ways to help students understand the underlying concepts, and student work.
We posed this question qualitatively to see what equations students might identify as useful, without asking them to substitute in exact values. One conclusion that the students needed to reach in order to successfully complete the activity is that the man and lady take the same amount of time in the death spiral, since they are interdependent. Additionally, in order to make conclusions about the distance, rate and time, students needed to use the equation, Distance = Rate x Time. A visual way of representing the man's and lady's rate of rotations in the death spiral is illustrated in the below Geometer's Sketchpad illustration, where the radii OA and OB rotate at a constant rate around the circumference of the circle centered at O, as shown in Figure 4.
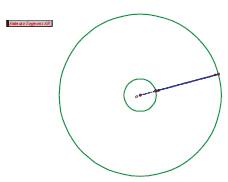
Figure 4. Geometer's Sketchpad animation of rotations in death spiral
One student responded, “Keauna travels faster as she is moving on bigger circle. Rockne is hardly moving.” While the student arrives at a correct conclusion, namely that Keauna travels faster, the justification of the solution is incomplete because it does not explain why traveling on a bigger circle necessitates a larger rate.
A more complete solution was stated in the following response: “Keauna. It takes both of them the same time to make one complete rotation, but the distance travelled in that time is greater for Keauna because her circle has a larger radius, which means a larger circumference. Since speed = distance / time, Keauna's greater distance implies greater speed.” This solution highlights the constant quantity, time, as the reason why speed and distance vary directly proportionally.
Another key idea in this activity involved the teachers' identifying relevant equations to describe the situation. In order to make conclusions about the distance, the circumference of a circle needed to be used.
An incorrect solution involved the student's using area of circle rather than circumference:

While computations with circles in the grade school curriculum often involve computing the circles' areas and circumferences, in this context the area of the circle relates to the amount of space on the ice that the pairs team needs in order to complete the death spiral. However, the question posed does not ask about the area the pairs team covers; it only asks about a comparison of the distances Keauna and Rockne travel.
A student correctly showed the below work to solve Question 2a:
Circumference of a circle =2πr where r is the radius of the circle.
Keauna distance 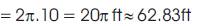
Rockne distance 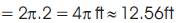
Keauna travels 16π ft further or approx. 50.27 ft further.

In order to help students determine whether to use area or circumference calculations, we developed the depicted Geometer's Sketchpad animation, in Figure 5, to show Keauna's and Rockne's arc lengths traveled at any given point in time after starting at OS.
Using this animation, students can see that the arc length SA representing Keauna's distance traveled along the arc is always greater than the arc length S'B representing Rockne's distance traveled during the death spiral.
Students who correctly identified the Distance = Rate x Time equation and who used the circumference of the circle to determine distance traveled answered this question correctly. A correct student's response is the following:
Keauna

Rockne
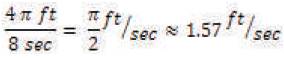
The differences in speeds are 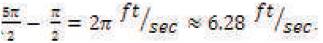
All of the students who solved the problem correctly used a method similar to the above, whereby they calculated Keauna's rate, then calculated Rockne's rate, and then found the differences.

Figure 5. Distances traveled by lady and man in death spiral (scale: 1 cm = 1 ft)
Lisa's method for calculating the difference in speeds by first determining the difference in radii is not an approach that the students used to solve questions 2a and 2b. The authors' goals for this question included 1) Having the students critique another solution to the problem, which in turn would help students “Construct viable arguments and critique the reasoning of others,”a Common Core State Standard for Mathematical Practice (CCSSI, 2010); 2) Having students connect between direct proportionality and the use of the distributive property; and 3) Having students connect between algebraic representations and geometric representations.
While the authors intended for students to observe that Lisa's method would produce a correct response, not all students attempted to use Lisa's method to find the solution that it would produce. One student incorrectly came to the following conclusion to question 2c:
“This is not a valid first step. Lisa did not consider that the distance formed by the death spiral is a circle and to find the distance, we calculate the circumference of each circle, then we can find the difference in their circumference.”
This student only saw one solution method possible, namely the method she suggests that Lisa should use.
Some students considered Lisa's method only to the extent to determine whether it would produce the same solutions as they obtained for questions 2a and 2b. One student responded to question 2c in the following way:
“So Lisa finds the difference to be 8 feet, which would aide her in finding the difference of their distance traveled which will still result in C = 2π 8 ft = 16π ft 50.27 ft
It will also aide in calculating the difference of their 2 speeds using D= RT

Using Lisa's method allows finding the solutions much quicker. Although using this method you do not know how far each traveled or the speed which may be necessary information.”
Consistent with Akyuz's (2012) suggestion to encourage efficient solutions, this student considers the efficiency with which calculations are made, as well as the information that is not determined using a more efficient solution. However, this student's solution still does not explain why Lisa's method generally works – for instance, if the values of the quantities in the problem were altered, we do not know whether the student would be able to determine whether Lisa's method would work without re-performing all of the calculations.
Some students solved the problem in a manner consistent with the authors' second goal of the question, namely by connecting direct proportionality and the use of the distributive property to show that Lisa's method was equivalent to methods which students previously used to solve the problem. For instance, one student found a more general solution method to question 2c, using the distributive property:
Lisa could use the difference between OA and OB to find Keauna and Rockne's speed. The distance they each travel create two circles. The distance they travel can be calculated by finding the circumference of each circle. The formula C = 2 r can be used to find the circumference. Keauna's distance is 2π K and Rockne's distance is 2π R when K = 0A and R = 0B. To find the difference in their distance, subtract their formulas:

If Lisa finds the differences between the radii of the circles, she could multiply the difference by 2π which would give her the differences between the distances they travel during the death spiral. Finally, if she divides the difference between their distances by 8, time, this would give her the difference between their rates of speed.
The solution shown above supports the idea that subtracting the circumferences of two circles isequivalent to finding the circumference of one circle whose radius was the difference of the two circles' radii (Posamentier, 2003).Only one of the students referred to a geometric interpretation of the difference between the two radii, which can represent the radius of a new circle, when responding to this problem. Her work is shown below:
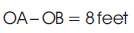
She could use this by using 8ft as the new “radius” to calculate the differences.
Circumference = 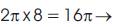 the difference of their distances
the difference of their distances
Rate = distance/time =  the difference between the speeds
the difference between the speeds
The student's idea that the new circle's “radius”is being transformed from the two original circles' radii can be illustrated using a Geometer's Sketchpad animation, as shown in Figure 6. The original two circles are “shrunken” simultaneously such that both circles' radii decrease by 2 feet. The circle with radius A has a radius that decreases from 10 feet to 8 feet. In the meantime, the circle with radius B has a radius that decreases from 2 feet to 0 feet, namely, the inner circle becomes just the point O.
In the snapshot above, the transformation is still taking place and the circle with radius OA is moving outwards towards the circle with the dotted line. The circle with radius OB is moving inwards towards point O. When the transformation finishes, the larger circle will have radius OA = 8 cm and the smaller circle will have radius OB = 0.

Figure 6. Transformation of two concentric circles (scale: 1 cm = 1 ft)
In this article, a mathematical modeling problem is presented in the context of figure skating and is illustrated using Geometer's Sketchpad software. The problem involves consideration of concentric circles' circumferences as distances traveled by the lady and man in a pairs death spiral, rates at which the lady and man travel, and the time that the death spiral takes. An alternate solution method is proposed for consideration; solving the problem in the proposed manner could involve using proportional relationships, the distributive property, and transformative reasoning. In the classroom, school children sometimes provide alternate solution paths than their teachers previously considered. Teachers' specialized content knowledge is evoked when they can evaluate the validity of student-invented methods (Ball, Thames and Phelps, 2008). In fact, research has shown that professional development activities that ask teachers to consider multiple solution paths can improve how teachers interpret and respond to students' thinking (Fennema et al, 2003).
Future work in mathematical modeling of sports activities could investigate interdisciplinary collaborations, such as incorporating mathematics and science, or mathematics and physical education. This work could be supported using technological tools such as spreadsheets and geometry software to help students and teachers envision the models in a dynamic environment.