Let G be a connected graph. A set D ⊆ V(G) is a point-set dominating set (psd-set) of G if for every set S ⊆ V – D, there exists a vertex v ∈ D such that the subgraph induced by S ∪ {v} is connected. The point-set domination number γp(G) of G is the minimum cardinality of a psd-set. This paper provides a comprehensive treatment of point set domination in graphs. First introduce the point-set domination number of a graph G, and determine this number for various known graphs. The relationship between set domination number with r point set domination number, point-set domination number and also few results regarding point-set are given as statements. Also In this paper the investigator say about global set-domination number γ_sg and global point-set domination number γ_pg of a graph G and determine these numbers for various known graphs and obtain some bounds for the graph G of diameters 3 and 4 in terms of γ. Finally the concept of the strong point-set domination number of a graph G is introduced, and its exact value is determined for some known graphs.

A set D - V (G) is said to be a strong point set dominating set (spsd set), if for every S - V - D there exists a vertex u2 D such that the subgraph hS [ {u}I induced by S [ {u}is connected and d(u)-d(s) for all s2 S where d(u) denote the degree of the vertex u. The minimum cardinality of an spsd set is called the strong point set domination number of G and is denoted by sp(G). A connected graph with atleast one cut vertex is called a separable graph. If B is a block of a separable graph G with psd set B0, then (V - B) [B0 is a psd set of G but need not be an spsd set of G as seen in the following discussion]. Hence the spsd sets of G are characterized first and then analysed with reference to the spsd sets of the blocks of G. The characterization of separable graphs with equal psd number and spsd number is derived. In the following discussion, a graph G always means a connected graph. Recently Kulli and Janakiram (2005) introduced the concept of global nonsplit domination. Let G and G be connected graphs. A set S µ V (G) is called a global nonsplit dominating set (GNSD-set) if S is an NSD-set of both G and G. The global nonsplit domination number °gns(G) of G is the minimum cardinality of a GNSD-set of G. Sampathkumar E. and Pushpa Latha L. (1993) define a set D of vertices in a connected graph G = (V,E) to be a point-set dominating (or, in short, psd-) set of G if for every subset S ⊆ V –D there exists a vertex v ∈ D such that the subgraph S ∪ {v}induced by the set S ∪ {v}is connected. The set of all psd-sets in G will be denoted Dps(G).

In graph theory, a dominating set for a graph G = (V, E) is a subset D of V such that every vertex not in D is adjacent to at least one member of D. The domination number γ(G) is the number of vertices in a smallest dominating set for G. (Sampathkumar E, 1989).

The dominating set problem concerns testing whether γ(G) ≤ K for a given graph G and input K; it is a classical NP-complete decision problem in computational complexity theory (Garey & Johnson 1979). Therefore it is believed that there is no efficient algorithm that finds a smallest dominating set for a given graph.

Let G be a graph with n ≥ 1 vertices and let Δ be the maximum degree of the graph. The following bounds on γ(G) are known (Haynes, Hedetniemi & Slater 1998,) One vertex can dominate at most Δ other vertices; therefore γ(G) ≥ n/(1 + Δ). The set of all vertices is a dominating set in any graph; therefore γ(G) ≤ n. If there are no isolated vertices in G, then there are two disjoint dominating sets in G; see domatic partition for details. Therefore in any graph without isolated vertices it holds that γ(G) ≤ n/2.

Definition 1 Let G be a connected graph. A set D ⊆ V(G) is a point-set dominating set (psd-set) of G if for every set S ⊆ V – D, there exists a vertex v ∈ D such that the subgraph induced by S∪{v}is connected. The point-set domination number γp(G) of G is the minimum cardinality of a psd-set. (Acharya, and Gupta, 2005).

Example 1 For the graph G given in Figure 1 D = {v₃, v₅}is a point-set dominating set of G and the point-set domination number γ_p(G) = 2.

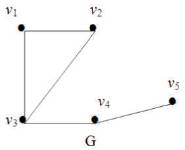
Figure 1.

Here D = {v₁, v₄} is domination set but not a point-set dominating set.

Example 2 Consider a path P_n and a cycle C_n on n = 5 and n = 8 vertices respectively.

Here D = {v₁, v₂, v₄}is a point-set dominating set of P₅ . Hence γ_p(P₅) = 3

D = { v₂ , v₃ , v₄ , v₅ , v₆ , v₈}is a point-set dominating set of C₈. Hence γ_p(C₈) = 6.

Remark 1 For a path P_n and cycle C_n on n ≥ 3 vertices γ_p(P_n) = n – 2,

γ_p(C_n) = n – 2. For n = 4, 5, γ_p(C_n) = 2, and γ_p(C_n) = n – 2 for n > 6.

Theorem 1 If G has a vertex of degree n – 1, then γ_p(G) = 1.

Proof. Let v be a vertex of degree n – 1. Let D ={v}, let S ⊆ V – D then clearly is connected and hence D is a psd-set with γ_p(G) = 1.

Corollary 1

• γ_p(K_n) = 1
• γ_p(K_{1, n}) = 1.

The following theorem gives an upper bound for γ_p(G).

Theorem 2 For any graph G, γ_p ≤ n – Δ where Δ is the maximum degree of G.

Proof. Let v be a vertex of maximum degree. Let S be a set of all vertices adjacent to v in G. Then it is clear that V – S is a point set domination set that is γ_p ≤ │V – S│ ≤ │V│–│S│= n – Δ . Hence γ_p ≤ n – Δ .

Theorem 3 Let D be a psd-set of a graph G, and u, v ∈ V – D. Then d(u, v) ≤ 2.

Proof. Let D be a psd-set of G. Let S = {u, v}. Since D is a psd-set, there exists a vertex x ∈ D such that the subgraph is connected. This implies d(u, v) ≤ 2.

Definition 2 A connected graph with no cut vertex is called a block.

Definition 3 A block graph is one in which every block is complete and in a cactus every block is either K₂ or a cycle.

Example 3 The graph G given in Figure 3 is a block graph with 3 blocks which are complete.

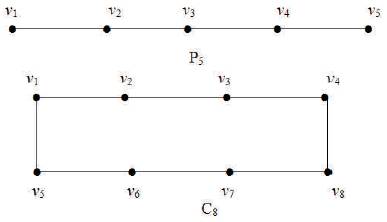
Figure 2.

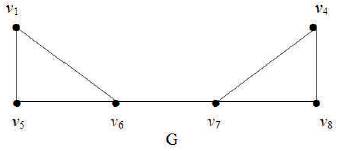
Figure 3.

Lemma 1 Let G = (V, E) be any graph and D be any point-set dominating set of G. Then  is a proper subset of a component H of G.

Remark 2 If H is a component of G then a point-set dominating set of H, together with the vertices of all its other components, forms a point-set dominating set of G.

Theorem 4 Let G be a finite graph of order n, and CG denote the set of its components. Then γ_p(G) = n – max{│V(H)│ – γ_p(H) : H ∈ C_G}.

Note 1 We now obtain the following major result from which we can deduce the exact values of γ_p for trees, block graphs and cactus.

Theorem 5 Let G be a graph with cut vertices. Then γ_p(G) = min{n –, n – k}, where k = max{│V(B)│ – γ_p(B), the maximum is taken over all the blocks B of G.

Lemma 2 Let G = (V, E) be any graph with cut vertices. D ∈ D_ps(G) and B ∈ B_G be such that V – D ⊆ V(B). Then every vertex of P(B, D) is adjacent to every other vertex of V – D.

Remark 3 Under the hypothesis of Lemma 2, we see that P(B,D) ≠ Ф  is complete.

Lemma 3 Let G = (V, E) be any graph with cut vertices, D ∈ D_ps(G) and B ∈ B_G be such that V – D ⊆ V(B).

Then V(B) ∩ D ≠ Ф V(B) ∩ D ∈ D_ps . (4)

Definition 4 A graph in which every block is either K₂ or a cycle is in a cactus.

Corollary 2 For a tree T, γ_p = n – Δ.

Corollary 3 If G is block graph or a cactus (≠C₅), then γ_p = n – Δ.

Definition 5 A set D ⊆ V is called a set dominating set (sd-set) if for every set T ⊆ V – D, there exists a nonempty set S ⊆ D such that the subgraph   is connected. The set-domination number γ_s(G) is the minimum cardinality of a set-dominating set.

Example 4 For the given graph in Figure 4 the set S = {v₁, v₃, v₆}is set-dominating set with minimum cardinality. Hence γ_s = 3.

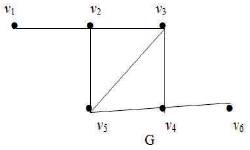
Figure 4.

Remark 4 Any psd-set of a graph G is a sd-set, and any sd-set is a dominating set. Hence γ ≤ γ_s ≤ γ_p.

Theorem 6 For any graph G γ_c =1 ≤ γ_s and diam G – 1 ≤ γ_s.

Theorem 7 If a graph G has an independent sd-set, then diam G ≤ 4. We now prove a similar results for for a psd-set.

Theorem 8 If a graph G has an independent psd-set D, then diam G ≤ 4.

Remark 5 The bound in theorem 08 can be strict. For example let G be a graph with exactly two blocks each block being C₄.

Then diam G = 4 and the set of vertices {v₃, v₄, v₅}of G where d(v₃, v₅ )= 4 and w is the cut vertex form an independent psd-set.

We now obtain a necessary condition for γ = γ_p.

Theorem 9 If γ(G) = γ_p(G), then diam G ≤ 4.

Definition 6 Let n ≥1 be an integer. A set D V is r-point set-dominating set (r-psd-set) of a graph G if for every set T ⊆ V – D there exists a nonempty set S ⊆ D containing at most r vertices that the subgraph is connected.

The r-point set-domination number γ_rp(G) of G is the minimum cardinality of an r-psd-set.

Result 1

• Every r-psd-set is a dominating set and γ_lp = γ_p. Also For 1 ≤ t ≤ r , γ_rp ≤ γ_lp ≤ γ_1p = γ_p.
• Since every r-psd-set is a set dominating set, we have γ_s ≤ γ_rp.
• If G is a path of order n, then γ_rp = n – 2 . For a cycle C_n we have γ_rp(C₃) = 1, γ_rp(C₄) = 2.

Note 2 For a vertex v, let N(v) be the set of all neighbours of v, and for a set S ⊆ V. Let N(S) = ∪ N(v) for all v S. Let k = max {│N(S)∩(V – S)│}where the maximum is taken over all sets S such that (a) │S│ £ r and (b) the subgraph  is connected.

Theorem 10: For any graph G of order n, γ_rp ≤ n – k.

Proof. Let S be a set of vertices satisfying the conditions (a) and (b) of the note 2, then clearly we have V – (N(S) – S) is an r-psd-set, and γ_rp ≤ n – k.

Theorem 11: For a tree T with n vertices, γ_rp ≤ n – k.

Remark 6

• B ∈ B_G, D ∈ D_ps⁰(G), V – D ⊆ V(B) and P(B, D) = Φ γ_p(G) = n – │V(B)│ + γ_p(B) where │V(B)│ – γ_p(B) = k.
• If D is a γ_p-set which is such that V – D ⊆ V(B) for some B B_G, then P(B, D) ≠ Φ │N(u) ∩ D│= 1 for every u∈ P(B, D) and every vertex of P(B, D) has degree Δ(G).
• Let D be a γ_p(G)-set such that V – D contains vertices of different blocks. Then V – D = N(w) for some vertex w of degree Δ(G).
• Δ(G) ≥ k(F) Þ V(G) – N(w) is a γ_p(G)-set for every vertex w of degree Δ(G).

For any separable graph G = (V, E) of order n,

let D_ps(G : X) = {D ∈ D_ps(G): there exist B ∈ B_G with V-D ⊂ V(B)}, D_ps (G:Y) = {D ∈ D_ps(G): there exists B ∈ B_G with V-D=V(B)}and D_ps (G:Z)=D_ps(G) - D_ps(G:X) ∪ D_ps(G:Y) = {D ∈ D_ps(G) : V – D contains vertices of different blocks }.

For simplicity, we call a psd-set a Type-X or Type-Y or Type-Z psd-set according to whether D is in D_ps(G, X), D_ps(G, Y) or D_ps(G, Z). We shall put D_ps⁰(G, X) = D_ps⁰(G) ∩ D_ps(G, X), D_ps⁰(G, Y) = D_ps⁰(G) ∩ D_ps(G, Y) and D_ps⁰(G, Z) = D_ps⁰(G) ∩ D_ps(G, Z).

D_ps(G) = D_ps(G, X) ∪ D_ps(G, Y) ∪ D_ps(G, Z) and D_ps⁰(G) = D_ps⁰(G, X) ∪ D_ps⁰(G, Y) ∪ D_ps⁰(G, Z).

Theorem 12 Let G be any connected graph to order n having cut vertices. Then D_ps⁰(G : Z) = Φ if and only if one of the following conditions holds:

• Δ(G) < k(G).
• Δ(G) = k(G) and every vertex of degree Δ has all its neighbours contained in a single block of G.

where k(G) : = k is as defined in theorem 05.

Remark 07 The above can be equivalently stated as follows:

Theorem 13 D_ps⁰(G : X₁) if and only if Δ(G) ≤ k(G).

Theorem 14 D_ps⁰(G : Y) ≠Φ if and only if

• Δ(G) ≥ k(G), and
• G has a block B which is a clique of order Δ(G) and = B⁺ where for any set A of vertices of G, N(A) denotes the set of neighbours of vertices in A and N[A] = A ∪N(A).

Theorem 15 D_ps⁰(G : Y)≠ Φ Δ(G) ≤ k(G) + 1.

Definition 7 A set D⊂ V is a set-dominating set (sd-set) if for every set S⊂ V – D, there exists a nonempty set T⊂ D such that the subgraph induced by S ∪ T is connected. The set-domination number γ_s = γ_s (G) is the minimum cardinality of a sd-set.

Definition 8 Let G be a co-connected graph. A set D ⊂ V is said to be a global set-domination set (g.sd-set) if it is a set-dominating set of both G and . The global-set domination number γ_sg = γ_sg(G) of G is the minimum cardinality of global set dominating set. (Sampathkumar, E., and Latha, L.P. 1994)

Example 5 For the graph G given in Figure 6 D = {v₂, v₃, v₅} is a global set-dominating set of G therefore γ_sg = 3.

Figure 5.

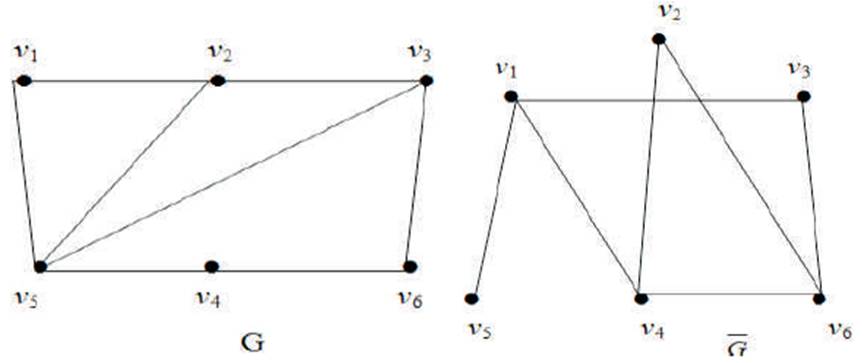
Figure 6.

Observation 1 For a path P_n on n ≥ 4 vertices, γ_sg = n – 2 for cycle C_n on n ≥ 6 vertices γ_sg = (C_n) = n – 3, whereas γ_sg = (C₅) = 3.

Theorem 16 In a tree T with p vertices and e end vertices, that is not star, the set of non-end vertices forms a minimum global sd-set and γ_sg = p – e.

Theorem 17 Let G be a co-connected graph of order p ≥ 4. Then, 2 ≤ γ_sg ≤ p – 2.

Proof, Let u and v be adjacent vertices of degree at least two (Such vertices clearly exist). Then V – {u, v}is a global sd-set of G, so γ_sg ≤ p – 2.

Theorem 18 For a graph G of order p, γ_sg = 2 if and only if diam G = diam   = 3, and either G or  has a bridge which is not an end edge.

Remark 8 For a graph G with cut vertices γ_c = γ_s. We now investigate graphs for which γs and γsg differ by at most one.

Theorem 19 Let G be a graph with cut vertices. Then γ_sg ≤ γ_s + 1 = γ_c + 1.

Theorem 20 Let G be a graph having diameter at least five, and let D ⊂ V(G). Then D is a minimal sd-set of G if and only if D is a minimal global sd-set of G.

Corollary 4 If diam G ≥ 5, then γ_s = γ_sg.

Theorem 21 Let G be a co-connected graph.

• When diam G =4, (a) γ_s ≤ γ + 1, and (b) γ_sg ≤ γ_s + 1.
• When diam G =3, (a) γ_g ≤ γ + 2, and (b) γ_sg ≤ γ_s + 2.

Remark 9 The bounds for γ_g and γ_sg in 1 and 2 are sharp. For example, for the graph G of diameter 4 in Figure 7 {u, v}is a γ-set whereas {u, v, y}is a γ_g-set.

Figure 7.

Thus, γ = 2 and γ_g = 3. Also {u, v, w}is a γ_s-set of G and {u ,v, w, y}is γ_sg-set. Hence γ_s = 3, γ_sg = 4.

For the graph H of diameter 3 in Figure 7

{a, b} Forms a γ-set as well as a γ_s-set, and the γ_g-set {a, b, c, d}is also a γ_sg -set. Thus, for H, γ = γ_s = 2 and γ_g = γ_sg = 4.

Remark 10 For any given positive integer n, there exist graphs of diameter two such that γ_g – γ = n, and γ_sg – γ_s = n. For example, if G = , then diam G = 2, γ_s = 2 and γ_sg = n + 2.

Similarly, for the graph H = 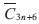, of diameter 2, we have γ = 2, and γ_g = n + 2.

Definition 9 For a con-connected graph G = (V, E), we define a set D ⊂V to be a global point-set dominating set (g.psd-set) if it is a point-set dominating set of both G and . The global point-set domination number γ_pg of G is defined as the minimum cardinality of a global psd-set.

Example 6 For the graph given in Figure 8 D = {v₂, v₄, v₅}is a global psd-set. Hence γ_pg= 3.

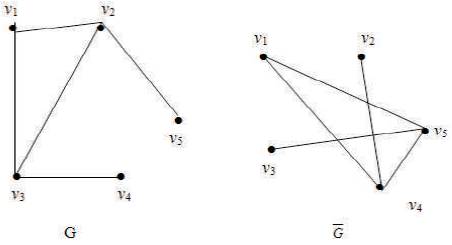
Figure 8.

Theorem 22 For a co-connected graph G.

• γ_g ≤ γ_pg
• γ_p ≤ γ_pg.

Theorem 23 Let G = (V, E) be a graph. A set D ⊂ V is a psd-set of G if and only if for every independent set W in V – D, there exists a vertex u in D such that W ⊂ N(u) ∩ (V – D).

Proposition 1 For a graph G, a set D ⊂ V(G) is a global psd-set iff the following conditions are satisfied:

• For every independent set W in V – D, there exists u in D such that, W ⊂ N(u) ∩ (V – D) in G.
• For every set S ⊂ V-D such that is complete in G, there exists v in D such that S ∩ N(v) = Φ in G.

From above proposition we obtain some bounds for γ_pg.

Lemma 4 y and v are the only vertices in G degree less than n – 2.

Theorem 24 For a graph G of order n ≥ 5, 3 ≤ γ_pg ≤ n – 2, and both bounds are sharp.

Theorem 25 If G is a graph with cut vertices, then γ_p ≤ γ_pg ≤ γ_p + 1.

Corollary 5 If G is a tree, a block graph or a cactus, n – Δ ≤ γ_pg ≤ n – Δ + 1.

Proof. Each of these graphs have cut vertices, and also by previous results we have γ_p = n – Δ.

Also we always have γ_p ≤ γ_pg .

Hence γ_p ≤ γ_pg ≤γ_p + 1 which implies n – Δ ≤ γ_pg ≤ n – Δ + 1.

Theorem 26 If G is a graph of diameter at least 4, then γ_pg = γ_p.

Corollary 06 For a tree T order n ≥ 4, γ_pg = n – Δ + 1 if diam (T) = 3, and γ_pg = n – Δ if diam (T) ≥ 4.

Remark 11 For graph with diameter 2, the difference between γp and γ can be made as large as we please. For example, γ_p() = 2, where γ_pg() = n – 2 for n ≥ 5.

Definition 10 Let G be a connected graph. A set D ⊆ V(G) is said to be a strong point-set dominating set of G if for every T⊆ V – D there exists a vertex d ∈ D such that the subgraph induced by T ∪ {d}is connected and deg d ≥ deg t for all t ∈ T. The strong point-set dominating number γ_sp of a graph G is the minimum cardinality of a strong point-set dominating set. (Swaminathan and Poovazhaki, 2002)

Example 7 For the graph G given in Figure 9 D = {v₁, v₃}is a strong point set dominating set.

Figure 9.

Result 2

If G has a vertex u of degree n – 1 then d = {u}is a strong point set and consequently γ_sp(G) = 1.

• γ_sp (k_{m, n}) = n if m > n
• γ_sp (k_{m, n}) =2
• γ_sp (P_n) = n – 2 for n ≥ 3
• γ_sp ( C_n) = n – 2 for n = 4, 5 and γ_sp ( C_n) = n – 2 for n ≥ 6.

Theorem 27 A subset D of V is an strong point-set dominating set if and only if for every independent set T⊆ V – D there exist d ∈ D such that T ⊆ N(d) and deg d ≥ deg t.

Proof. If D ∈ D_sp(G) (set of all strong point-set domination sets) then the condition follows from the definition of D. Conversely, suppose the condition is satisfied. Let T₁ ⊆ V – D be any set.

If T is independent then by the given condition there exist a d ∈ D such that T ⊆ N(d) and deg d ≥ deg t for all t ∈ T.

If T is not independent, let T = T₁ ∪ T₂. Where T₁ is a maximal independent subset of T. Let t' ∈ T be such that deg t' = max {deg t}.

Case(i): t' ∈T₁

T₁ is maximal independent subset of T implies there exist a d ∈D such that T₁ ⊆ N(d) and deg d ≥ deg t for all t ∈ T₁.

Also T₁ is maximal independent subset of T implies every vertex of T₂ is adjacent to at least one vertex in T₁.

Hence  is connected also deg d ≥deg t' implies deg d ≥ deg t for all t ∈ T. Hence  is connected and deg d ≥ deg t for all t ∈ T.

Case(ii): t' ∈ T₂

t'∈ T₂ implies t' is adjacent to atleast one vertex in T₁.

Subcase (i): t' is adjacent to all vertices in T₁.

Also we have every vertex of T₂ is adjacent to atleast one vertex in T₁.

By the given condition as {t'}is independent there exist d ∈ D such that dt' ∈E(D) and deg d ≥ deg t'.

Hence  is connected and deg d ≥ deg t' ≥ deg t for all t ∈ T. Hence is connected and deg d ≥ deg t for al t ∈ T.

Subcase (ii): There are vertices in T₁. Which are not adjacent to t'.

Let A = {t ∈ T₁ / t∈N(t')}{t'}.

Then A is independent. By the given condition there exist d ∈ D such that is connected and deg d ≥ deg a for all a ∈ A. Hence is connected and deg d ≥ deg t' (since t' ∈A).

Therefore is connected and deg d ≥ deg t' ≥ deg t for all t ∈ T. Hence D ∈ D_sp(G).

Definition 11 A set D ∈ D_sp(G) is minimal if for every d ∈ D, D – {d}is not a strong point-set dominating set.

Theorem 28 D ∈ D_sp(G) is minimal if and only if each d ∈ D satisfy one of the following three conditions.

• N(d) ∩ (D – {d}) = Φ.
• There exist an independent set T ⊆ V – D , for t ∈ T such that (∩N(t)) ∩ D = {d}(or) if there exist d₁∈ (N(t)) ∩ D – {d}. Then deg d₁ < deg t for some t ∈ T.
• Such that T ⊄ N(d) ∩ (D – {d}) such that T₁ ⊂N(d₁) then deg d₁ < deg t for some t ∈T₁ (or) deg d₁ < deg d.

Proof : If D ∈ D_sp(G) is minimal then D – {d}is not an strong point set dominating set for each d ∈ D.

Let T ⊆ V – D ∪ {d}.