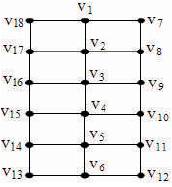
Figure 1. Super Strongly Perfect Graph
A Graph G is Super Strongly Perfect Graph if every induced subgraph H of G possesses a minimal dominating set that meets all maximal cliques of H. In this paper, the authors have given a characterization of Super Strongly Perfect graphs. Using this characterization they have characterized the Super Strongly Perfect graphs in Ladder graphs. They have investigated the structure of Super Strongly Perfect Graphs in Ladder graphs. Also they have found the relation between domination number, co-domination number and diameter of Ladder Graphs.
Graph theory is one of the important parts of mathematics which becomes increasingly significant as it is applied to other areas of mathematics, science and technology. It is being actively used in fields as varied as biochemistry (genomics), electrical engineering (communication networks and coding theory), computer science (algorithms and computation) and operations research (scheduling). The powerful combinatorial methods found in graph theory have also been used to prove fundamental results in other areas of pure mathematics [Bondy and Murty (1976)]. Super Strongly Perfect graph (SSP) is defined by B. D. Acharya and its Characterization has been given as an open problem [Murty (2006)]. Many characterizations of Super Strongly Perfect graphs have been done [Amutha and Mary Jeya Jothi (2012)]. Among all characterizations of SSP, the characterization by bipartite graph plays an important role. In this line of thought, here the authors are considering Ladder graphs which are bipartite. The interesting problem of topological chirality has been solved by applying the topological symmetry concept to the molecular mobius ladders [Skiena (1990)].
In this paper, graphs are finite and simple, that is, they have no loops or multiple edges. Let G = (V, E) be a graph. A Clique in G is a set X⊆ V (G) of pair wise adjacent vertices. A subset D of V (G) is called a dominating set if every vertex in V - D is adjacent to at least one vertex in D. A subset S of V is said to be a minimal dominating set if S - {u} is not a dominating set for any u∈S. A Path is a walk (A Walk on a graph is an alternating series of vertices and edges, beginning and ending with a vertex, in which each edge is incident with the vertex immediately preceding it and the vertex immediately following it) in which all vertices are distinct. A Path graph on n vertices is denoted by Pn. The Cartesian graph product G = G1xG2 , (sometimes simply called “the graph product”) of graphs G1 and G2 with disjoint point sets V1 and V2 and edge sets X1 and X2 is the graph with point set V1xV2 and u = (u1 ,u2 ) adjacent with v = (v1 , v2 ) whenever u1 = v1 and u2 is adjacent to v2 or u2 = v2 and u1 is adjacent to v1.
In this paper, the authors have given the characterization of Super Strongly Perfect graphs in Ladder graphs. They have discussed the structure of Super Strongly Perfect Graphs in Ladder graphs as shown in Figure 1. Also, they have studied the domination number, co-domination number and diameter of Ladder Graphs.
A Graph G = (V, E) is Super Strongly Perfect if every induced sub graph H of G possesses a minimal dominating set that meets all maximal cliques of H. Figures 1 and 2 illustrates the definition of Super Strongly Perfect Graph.

Figure 1. Super Strongly Perfect Graph
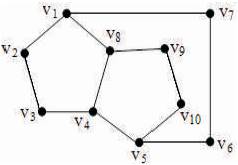
Figure 2. Non-Super Strongly Perfect Graph
In Figure 1, {v1 , v3 , v5 , v8 , v10 , v12 , v13 , v15 , v17} is a minimal dominating set which meets all maximal cliques of G.
In Figure 2, {v1 , v3 , v6 , v9 } is a minimal dominating set which does not meet all maximal cliques of G.
Since the characterization of Ladder graphs are obtained by using bipartite graphs, the characterization of bipartite graphs are given below.
Figure 3 shows the bipartite graph (or bigraph) whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V. A graph is bipartite if and only if it does not contain an odd cycle [Foulds (1994)]. Figure 3 illustrates the bipartite graph which is SSP.
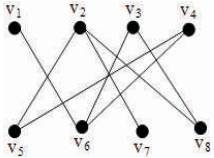
Figure 3. Bipartite graph
In Figure 3, {v2 , v5 , v6 , v8 } is a minimal dominating set which does not meet all maximal cliques of G.
Let G be graph with maximal complete sub graph K2 . Then G is bipartite if and only if it is Super Strongly Perfect.
From the above theorem, the authors have given the characterization of Super Strongly Perfect Graphs using bipartite graphs. By this, the authors are analysing the Ladder Graphs by the following theorem.
An n-Ladder graph Ln can be defined as P2xPn, where Pn is a path graph on n vertices [3]. Hosoya and Harary also use the term “ladder graph” for the graph Cartesian product K2 x Cn , where K2 is the complete graph on two vertices and Cn is the cycle n graph on n vertices [Hosoya and Harary (1993)]. This class of graph is however more commonly known as a prism graph. A family of ladder graphs is studied which is characterized in terms of relations, called connective relations, on finite, totally ordered sets [Rogers (1982)]. Every ladder graph is bipartite. Figure 4 illustrates the Ladder graph which is SSP.

Figure 4. Ladder Graph – P6 x K2
In Figure 4, {v1, v3, v5, v7, v9, v11} is a minimal dominating set which meet all maximal cliques of G.
Every Ladder Graph is Super Strongly Perfect.
Let G be a Ladder Graph.
⇒G is bipartite.
Now, by the theorem 4.1, G is Super Strongly Perfect.
Hence every Ladder Graph is Super Strongly Perfect.
Due to the characterization of ladder graphs, the various structural properties of ladder graphs have been found and it is given below
Every Ladder Graph which is Super Strongly Perfect is 2-colourable.
Let G be a Ladder Graph which is Super Strongly Perfect.
⇒ By the construction of the graph, there exists a partition (V1 , V2 ) such that the vertices in V1 are non adjacent. Also the vertices in V2 are non adjacent.
⇒ The vertices in V1 are coloured with a colour 1 and the vertices in V1 are coloured with a colour 2, since there is an adjacency between the vertex sets V1 and V2 .
⇒ G is 2-colourable.
Hence every Ladder Graph is 2-colourable.
Let G be a Ladder Graph which is Super Strongly Perfect, then diam (G) ≥ 3 if and only if 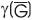 = 2.
= 2.
Let G be Ladder Graph which is Super Strongly Perfect.
Assume diam (G) ≥ 3.
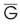 are either adjacent to u or v.
are either adjacent to u or v.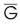
Since G has no isolated vertex 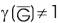
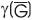 =2
=2Conversely assume that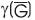 =2
=2
Let D = {u, v}be a minimum dominating set of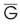
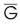 are either adjacent to u or v.
are either adjacent to u or v.Then there does not exist a vertex in G which is adjacent to both u and v.
Hence proved.
Let G be a Ladder Graph which is Super Strongly Perfect then  >1 if and only if diam
>1 if and only if diam 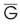 ≤ 3.
≤ 3.
Let G be a Ladder Graph which is Super Strongly Perfect.
Assume diam 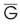 ≤ 3.
≤ 3.
To prove  >1
>1
Suppose 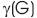 =1
=1
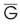
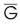 cannot be defined, which is a contradiction to the assumption.
cannot be defined, which is a contradiction to the assumption.Conversely assume that  >1
>1
To prove diam 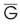 ≤ 3
≤ 3
Suppose diam 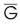 > 3.
> 3.
Then there exists atleast two vertices u, v in 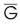 with d (u,v) > 3 in
with d (u,v) > 3 in 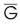
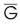 has no vertex which is adjacent to both u and v.
has no vertex which is adjacent to both u and v.All the vertices are either adjacent to u or v in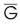
 <2which is a contradiction to the assumption.
<2which is a contradiction to the assumption.Hence 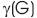 >1
>1
Let G be a Ladder Graph which is Super Strongly Perfect then 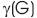 >1 if and only if
>1 if and only if  =2
=2
Let G be a Ladder Graph which is Super Strongly Perfect.
Assume  =2
=2
Let D = {u, v}be a minimum dominating set of 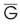
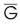
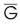
 >1
>1Conversely assume that 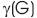 >1
>1
To prove  =2
=2
Since 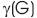 >1
>1
Since G is Bipartite, there exists a bipartition (V1 , V2 ) in G, and all the vertices are mutually non adjacent in V1 and V2 .
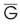 all the vertices in V1 and V2 are mutually adjacent and there exists at least one adjacency between any two vertices u, v such that U ∈V1 v∈ V2
all the vertices in V1 and V2 are mutually adjacent and there exists at least one adjacency between any two vertices u, v such that U ∈V1 v∈ V2 =2
=2Hence proved.
Every Ladder Graph which is Super Strongly Perfect contains a minimal dominating set of maximum cardinality 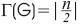 , where n is the number of vertices in the Ladder Graph.
, where n is the number of vertices in the Ladder Graph.
Every Ladder Graph which is Super Strongly Perfect has 3n – 2 (where n is the number of vertices) maximal cliques K2 and it contains n-1 squares.
The authors have investigated the Super Strongly Perfectness in Ladder graphs. Also, they have studied the domination number, co-domination number and diameter of Ladder Graphs. This investigation is worth considering for the remaining architectures also.