On A New Sequence Space Related To lρ
Keywords :
- Sequence Space,
- BK- Space,
- Schauder Basis,
- Matrix Mapping.
Introduction
By ω, the authors denote the space of all real or complex valued sequences. Any vector subspace of ω is called a sequence space.
We shall write l∞ ,c and c0 for the sequence spaces of all bounded, convergent and null sequences, respectively, which are BK- spaces with the same norm given by
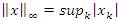
for all k ∈ N. Also, by lp(0 < p < ∞) we denote the sequence space of all sequences associated with p -absolutely convergent series. It is known that lp is a complete p- normed space and a BK- space in the cases of 0 < p < 1 and 1 ≤ p < ∞ with respect to the usual p- norm and lp - norm defined by
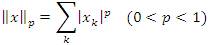
and
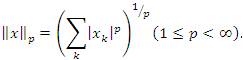
A sequence space X with a linear topology is called a K- space provided each of the maps pn : X → C defined by pn (x) = xn is continuous for all n ∈ N, where C denotes the complex field and N = {0,1,2.....} A K- space X is called an FK- space provided X is a complete linear metric space. An FK- space whose topology is normal is called a BK- space.
Let X and Y be sequence spaces and A = (ank) be an infinite matrix of real or complex numbers (ank) , where n, k ∈ N. Then, we say that A defines a matrix mapping from X into Y if for every sequence x = (xk)∈ X the sequence Ax = {An(x)}, the A - transform of x, exists and is in Y, where
By (X,Y), we denote the class of all infinite matrices that map X into Y. Thus, A ∈ (X,Y) if and only if the series on the right side of (1) converges for each n∈N and every x∈X and Ax∈Y for all x∈X.
For a sequence space X, the matrix domain of an infinite matrix A in X is defined by
which is a sequence space.
We shall write e(k) for the sequence whose only non-zero is a 1 in the kth place for each k∈ N
Throughout this paper, let λ=(λk)∞k=0 be a strictly increasing sequence of positive reals tending to ∞ , that is
We shall use the convention that any term with a negative subscript is equal to zero, e.g., λ-1=0 and x-1 = 0.
We define the infinite matrix Δ=(λnk)∞n,k=0 by
for all k∈ N. Then, for any sequence x=(xk)∈ω, the Λ - transform of x is the sequence Λ(x)={Λn(x)}, where
for all n∈ N. It is obvious that by (4) that the matrix Λ=(λnk)is a triangle, i.e., λnn ≠ 0 and λnn = 0 for all k > n(n∈N) . The idea of constructing a new sequence by means of the matrix domain of a particular limitation method has recently been studied by several authors, e.g., Altay and Başar [2], Mursaleen et all [3,14], Mursaleen and Noman [15,16,17], Malkowsky [12], Malkowsky and Savaş [13].
1. Main Results
In this section the authors introduce a new sequence space, as the sets of all sequences whose Λ - transforms is in the space lp(u) where 0 < p < ∞ and (un) is a sequence of positive real numbers, that is
With the notation of (2), we can redefine the space lλp(u) as follows:
lλp(u) = lp(Λ, u).
Theorem 1.1.
We have the following:
- If 0 < p < 1, then lλp(u) is a complete p- normed space with the p- norm
- If 1 ≤ p < ∞, then lλp(u) is a BK- space with the norm
2. Some Inclusion Relations
In the present section, the authors give some inclusion relations concerning lλp the space and lp.
Lemma 2.1.
For any sequence x=(xk)∈ ω, the equalities
hold, where S(x)={Sn(x)} is the sequence defined by
Lemma 2.2.
For any sequence λ=(λk)∞k=0 satisfying (3), we have
It is obvious that Lemma 2.2 still holds if the sequence 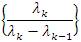 is replaced by
is replaced by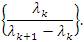
Let u = (un) be a bounded sequence of positive real numbers. Then, we have the following theorems, lemmas and n corollaries.
Theorem 2.3.
If 0 < p < q < ∞ then the inclusion lλp(u)⊂ lλq(u) strictly holds Proof. Let 0 < p < q < ∞. Then, it follows by the inclusion lp ⊂ lq that the inclusion lλp(u)∈ lλp(u) holds. Further, since the inclusion lp∈ lq is strict, there is a sequence x = (xk ) in lq but not in lp Define the sequence y = (yk) in terms of the sequence x as follows:
Then, we have for every n ∈ N that
This shows that Λ(y) = x, hence Λ(y)∈ lp\ lq and since u = (un) is a bounded sequence we have y is in lλq(u), but not in lλp(u). Therefore, the inclusion lλp(u) ⊂ lλq(u) is strict. This completes the proof.
Lemma 2.4.
The inclusion lλp(u) ⊂ lq holds if and only if S(x)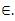 (lp) only if for every sequence x ∈ lλp(u), where 0 < p < ∞.
(lp) only if for every sequence x ∈ lλp(u), where 0 < p < ∞.
Proof. Suppose that the inclusion lλp(u) ⊂ lp holds and take any x = (xk)∈ lλp(u), Then x∈ lp by the hypothesis. Since x ∈ lλp(u) and u = (un) is a bounded sequence||Λ||p < ∞ we have
So, we have S(x)∈ lp.
Conversely, let x ∈ lλp(u) Then, we have by the hypothesis that S(x)∈ lp. It follows by (6) that
Hence, the inclusion holds and this completes the proof.
Lemma 2.5.
If 1/λ∉ lp then the neither of lλp(u) and lp includes the other one, where 0 < p < ∞.
Proof. Suppose that 1/λ∉ lp where 0 < p < ∞ and consider the sequence x=e(0) =(1,0,0,...)∈ lp . Then, we have for every n∈N that
Then, we have Λ(x)∉ lp and since u = (un) is a bounded sequence we have x∈ lλp(u). Thus, the sequence x is in lp, but not in lλp(u).
On the other hand, let 1 ≤ p < ∞ and define the sequence y=(yk) by
for all k∈ N. Since 1/λ∉ lp , we have y∉ lp . Then, we have for every n ∈ N that
and hence
Then, we have Λ(y)∈ lp and y∈ lλp(u). Thus the sequence y is in lλp(u), but not in lp where 1 ≤ p < ∞.
Lemma 2.6.
If the inclusion lp ⊂ lλp(u) holds, then 1/λ∈ lp for 0 < p < ∞.
Proof.
Suppose that the inclusion lp ⊂ lλp(u) holds, where 0 < p < ∞, and consider the sequence x = e(0)= (1,0,0,....)∈ lp . Then x ∈ lλp(u) Thus we obtain that
Then, we have 1/λ∈ lp and this completes the proof.
Lemma 2.7 If 1/λ∈ l1 , then
Theorem 2.8.
The inclusion l1⊂ lλ1(u) holds if and only 1/λ∈l1.
Proof.
The necessity is immediate by Lemma 2.6
Conversely, suppose that 1/λ∈ l1 Then M =  by Lemma 2.7. Let x = (xk)∈ l1 be given. Then, we have
by Lemma 2.7. Let x = (xk)∈ l1 be given. Then, we have
Since u = (un) is a bounded sequence we have X∈ lλp(u) Hence, the inclusion l1 ⊂ lλ1(u).
Corollary 2.9.If 1/λ∈ l1 , then the inclusion lp ⊂ lλp(u) holds for 1 ≤ p < ∞.
Proof. The inclusion trivally holds for p = 1 which is obtained by Theorem 2.8. Let 1 < p < ∞ and take any x=(xk)∈ lp Then, for every n∈ N, we have by applying the Hölder's inequality that
Hence, we have that
where M= by Lemma 2.7. This shows that x∈ lλp(u).
by Lemma 2.7. This shows that x∈ lλp(u).
Corollary 2.10.
The inclusion lp ⊂ lλp(u) holds if and only if 1/λ∈ lp , where 1 ≤ p < ∞.
Proof.
The necessity is immediate by Lemma 2.6.
Conversely, suppose that 1/λ∈ lp where 1 ≤ p < ∞ Then 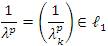 . Then, we have by Lemma 2.7 that
. Then, we have by Lemma 2.7 that
Further, we have for every fixed k, n∈ N that
Thus, we obtain that
Therefore, we have e(k)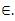 lλp(u).
lλp(u).
Lemma 2.11.
Let x=(xk) be a positive real sequence such that lim in fk →∞ Xk =0 Then, for every positive number 0 < p < ∞ there is a subsequence x(p)=(xk)∞r=0 of x, depending on p, such that kr+1 - kr ≥ 2 for all r∈ N and 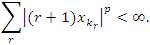
Theorem 2.12. The inclusion lp⊂ lλp(u) strictly holds if and only if 1/λ∈ lp and 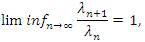 where 1 ≤ p < ∞.
where 1 ≤ p < ∞.
Proof. Suppose that the inclusion lp ⊂ lλp(u) is strict, where 1 ≤ p < ∞. Then, the necessity of the first condition is immediate by Lemma 2.6. Further, since the inclusion lλp(u)⊂ lp cannot be hold, Lemma 2.4 implies the existence of a sequence x∈ lλp(u) such that 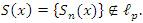 Since x∈ lλp(u), we have
Since x∈ lλp(u), we have 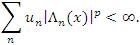 Thus, it follows by applying the Minkowski's inequality that
Thus, it follows by applying the Minkowski's inequality that 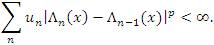 This means that
This means that 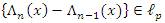 and since {Sn(x)}∉ lp it follows by the relation (7) that
and since {Sn(x)}∉ lp it follows by the relation (7) that 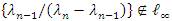 and hence
and hence 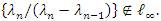 Thus, we have by Lemma 2.2 to the necessity of the second condition
Thus, we have by Lemma 2.2 to the necessity of the second condition
Conversely, since 1/λ∈ lp we have by Corollary 2.10 that the inclusion lp ⊂ lλp(u) holds. Further, since 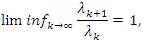 we obtain by Lemma 2.2 that
we obtain by Lemma 2.2 that
Let us now define the sequence y = (yk) for every k,r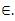 N by
N by
Then, it is clear that y∉ lp On the other hand, we have for every n,r∈ N that
This and (8) imply that Λ(y)∈ lp and hence Y∈ lλp(u). Thus, the sequence y is in lλp(u) but not in lp.
Theorem 2.13. The equality lλp(u) = lp holds if and only if 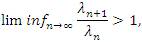 where 1 ≤ p < ∞
where 1 ≤ p < ∞
Proof. The necessity follows from Theorem 2.12. For, if the equality holds, then the inclusion lp ⊂ lλp(u) holds and hence 1/λ∈lp by Lemma 2.6. Further, since the inclusion lp ⊂ lλp(u) cannot be strict, we have Theorem 2.12 that 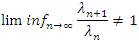 and Hence
and Hence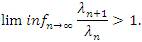
Conversely, suppose that 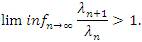 Then, there exists constant a >1 such that
Then, there exists constant a >1 such that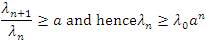 for all n∈ N. This shows that 1/λ∈ l1 which leads us with Corollary 2.9 to the inclusion lp⊂ lλp(u) holds where 1 ≤ p < ∞ . On the other hand, we have by Lemma 2.2 (b) that
for all n∈ N. This shows that 1/λ∈ l1 which leads us with Corollary 2.9 to the inclusion lp⊂ lλp(u) holds where 1 ≤ p < ∞ . On the other hand, we have by Lemma 2.2 (b) that 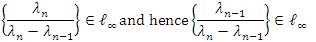 .
.
Let X ∈ lλp(u), then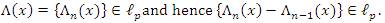 Thus, we obtain by the relation (7) that
Thus, we obtain by the relation (7) that  Therefore, we have by Lemma 2.4 that the inclusion lλp(u)⊂ lp. By combining the inclusion
Therefore, we have by Lemma 2.4 that the inclusion lλp(u)⊂ lp. By combining the inclusion 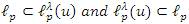 we get the equality
we get the equality 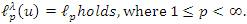
This completes the proof.
References
[1]. Altay, B., & Başar, F. (2003). On the space of sequences of p- bounded variation and related matrix mappings. Ukrainian Math. J., 55(1), 136-147.
[2]. Altay, B.,& Başar, F. (2005). Some Euler sequence spaces of non- absolute type. Ukrainian Math. J., 57(1), 1-17.
[3]. Altay, B., Başar, F., & Mursaleen, M. (2006). On the Euler sequence spaces which include the spaces l and l I. Inform. Sci,176(10), 1450-1462.
[4]. Aydın, C., & Başar, F. (2004). On the new sequence spaces which include the spaces c and c. Hokkaido Math. J., 33(2), 0 383-398.
[5]. Aydın, C., & Başar, F. (2004). Some new difference sequence spaces. Appl. Math. Comput., 157(3), 677-693.
[6]. Aydın, C., & Başar, F. (2004). Some new paranormed sequence spaces. Inform. Sci.,160(1-4), 27-40.
[7]. Aydın, C., & Başar, F. (2005). Some new sequence spaces which include the spaces l and l . Demonstratio Math., 38(3), 641-656.
[8]. Başarır, M. (1995). On some new sequence spaces and related matrix transformations. Indian J. Pure Appl. Math., 26(10), 1003-1010.
[9]. Choudhary, B.,& Nanda, S. (1989). Functional Analysis with Applications. John Wiley & Sons Inc., New Delhi.
[10]. Hardy, G. H., Littlewood, J. E., & Polya, G. (1952). Inequalities. Cambridge University Press.
[11]. Maddox, I. J. (1988). Elements of Functional Analysis (2nd ed). Cambridge University Press.
[12]. Malkowsky, E. (1997). Recent results in the theory of matrix transformations in sequence spaces. Mat. Vesnik, 49, 187- 196.
[13]. Malkowsky, E.,& Savaş, E. (2004). Matrix transformations between sequence spaces of generalized weighted means. Appl. Math. Comput., 147(2), 333-345.
[14]. Mursaleen, M., Başar F., & Altay, B. (2006). On the Euler sequence spaces which include the spaces l and l II. Nonlinear Analysis: TMA, 65(3), 707-717.
[15]. Mursaleen, M., & Noman, A. K. (2010). On the spaces of - convergent and bounded sequences. Thai J. Math. 8(2), 311-329.
[16]. Mursaleen, M.,& Noman, A. K. (2010). On some new difference sequence spaces of non-absolute type. Math. Comp. Mod., 52(3-4), 603-617.
[17]. Mursaleen, M.,& Noman, A. K. (2011). On some new sequence spaces of non-absolute type related to the spaces l and l I. Filomat, 25(2), 33-51.
[18]. Ng, P.- N. (1978). On modular space of a nonabsolute type. Nanta Math. 2, 84-93.
[19]. Ng, P.- N., & Lee, P.-Y. (1978). Cesàro sequence spaces of non- absolute type, Comment. Math. Prace Mat., 20(2), 429- 433.
[20]. Wilansky, A. (1984). Summability through Functional Analysis. North- Holland Mathematics Studies, 85.
[21]. Wang, C. - S. (1978). On Nörlund sequence spaces. Tamkang J. Math., 9, 269-274.
![]() where
where ![]() is a strictly increasing sequence of positive reals tending to ∞ , u = (un) is a sequence of positive real numbers and 0 < p< ∞. They also study some inclusion relations concerning the space
is a strictly increasing sequence of positive reals tending to ∞ , u = (un) is a sequence of positive real numbers and 0 < p< ∞. They also study some inclusion relations concerning the space ![]() .
.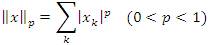
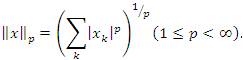
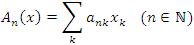
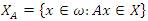
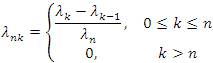
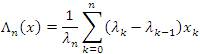
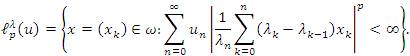
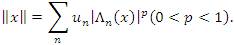
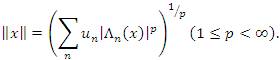



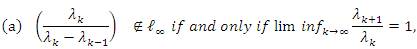
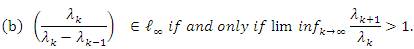

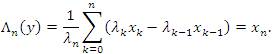
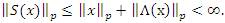
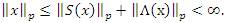

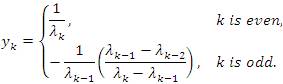
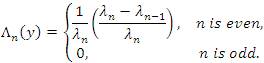
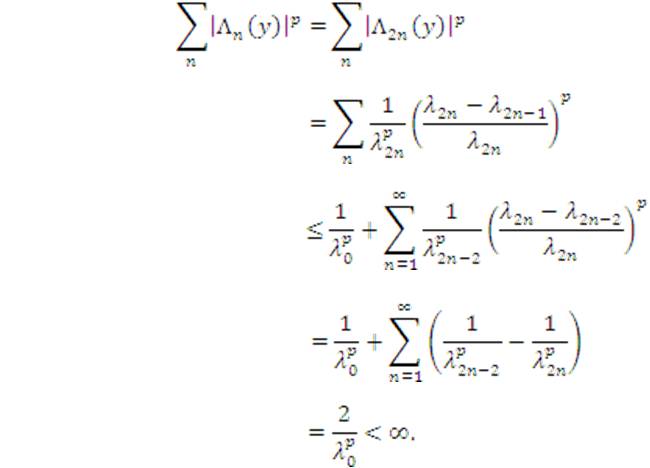



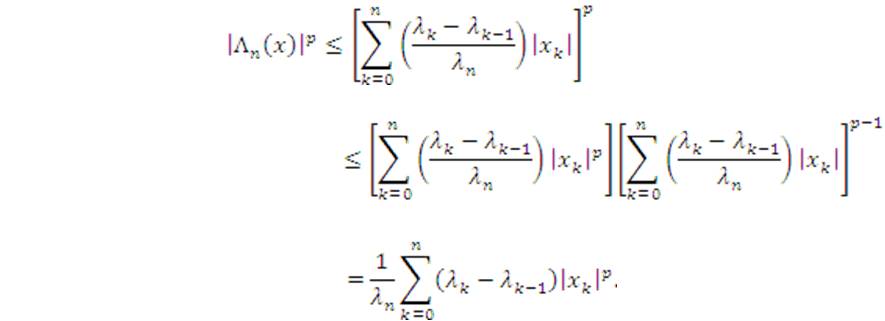
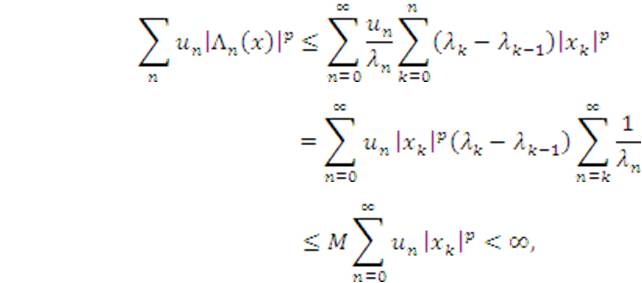
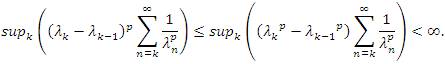
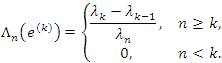
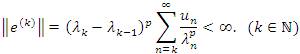
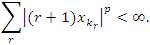
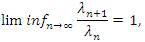 where 1 ≤ p < ∞.
where 1 ≤ p < ∞.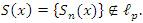 Since x∈ lλp(u), we have
Since x∈ lλp(u), we have 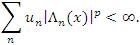 Thus, it follows by applying the Minkowski's inequality that
Thus, it follows by applying the Minkowski's inequality that 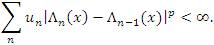 This means that
This means that 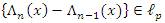 and since {Sn(x)}∉ lp it follows by the relation (7) that
and since {Sn(x)}∉ lp it follows by the relation (7) that 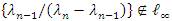 and hence
and hence 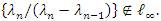 Thus, we have by Lemma 2.2 to the necessity of the second condition
Thus, we have by Lemma 2.2 to the necessity of the second condition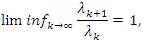 we obtain by Lemma 2.2 that
we obtain by Lemma 2.2 that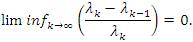
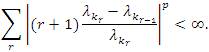
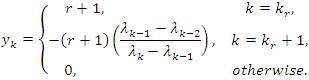
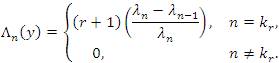
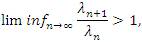 where 1 ≤ p < ∞
where 1 ≤ p < ∞ 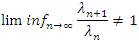 and Hence
and Hence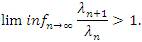
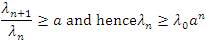 for all n∈ N. This shows that 1/λ∈ l1 which leads us with Corollary 2.9 to the inclusion lp⊂ lλp(u) holds where 1 ≤ p < ∞ . On the other hand, we have by Lemma 2.2 (b) that
for all n∈ N. This shows that 1/λ∈ l1 which leads us with Corollary 2.9 to the inclusion lp⊂ lλp(u) holds where 1 ≤ p < ∞ . On the other hand, we have by Lemma 2.2 (b) that 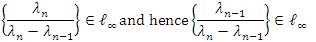 .
.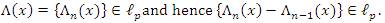 Thus, we obtain by the relation (7) that
Thus, we obtain by the relation (7) that  Therefore, we have by Lemma 2.4 that the inclusion lλp(u)⊂ lp. By combining the inclusion
Therefore, we have by Lemma 2.4 that the inclusion lλp(u)⊂ lp. By combining the inclusion 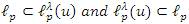 we get the equality
we get the equality