Figure 1. Lossy transmission line
The present paper is devoted to investigation of lossy transmissions lines terminated by a nonlinear resistive element. The transmission line is terminated by an R-element with exponential nonlinearity in the V-I characteristic. The reducing of the mixed problem for Telegrapher hyperbolic system to an initial value problem for a nonlinear neutral equation on the boundary is made [3]. The nonlinearity in the boundary condition is transferred to the neutral equation on the boundary. Then the authors introduce a suitable operator whose fixed point is an oscillatory solution of the neutral equation. The main existence-uniqueness theorem contains conditions which guarantee that the operator mentioned is contractive one in a uniform space. Finally, they demonstrate how to apply the results obtained to the circuit design.
Recently transmission lines theory has received renewed attention. This is because the transmission line theory has found new and important applications in the area of high-speed VLSI interconnections [1]. In many applications, transmission lines are connected to nonlinear circuits (cf. [1-5]). In a recent paper [6] we have investigated oscillation regimes in lossless transmission lines terminated by R-load with polynomial V-I characteristic. Here we consider the same problem for a lossy transmission line terminated by R-load with exponential V-I characteristic.
The study of the problem of oscillations in transmission lines starts with the first results given in [7-9]. The main goal of the present paper is to extend the fixed point method from periodic to oscillatory problems. The authors demonstrate also that this method could be applied not only to neutral equations with polynomial nonlinearities but to neutral equations with exponential ones as well. The reducing of the mixed problem for Telegrapher equations to an initial value problem for a neutral equation in [10] is made. The basics of the fixed point theory are exposed in [11,12]. An essential role plays the appropriate choice of functional spaces, extension of Bielecki norm and introduction of a suitable operator whose fixed points are oscillatory solutions of the neutral equation. The applicability of loads with exponential characteristics are given in [13,14].
The authors proceed from the circuit shown on Figure 1 where E is the source function, Ro and Co – linear loads, while the resistive load at the right end has a nonlinear V-I characteristics with exponential nonlinearity.
Figure 1. Lossy transmission line
It is known that if the frequency increases, the lossy could not be neglected. The lossy transmission line is described by the following first order linear hyperbolic system of partial differential equations (Telegrapher equations):
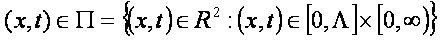
where u(x,t) and i(x,t) are the unknown voltage and current, L is per-unit-length inductance representing the magnetic flux passing between the conductors due to the current on those conductors, C − per-unit-length capacitance representing the displacement current flowing between the two conductors, R − per-unit-length resistance and G − per-unit-length conductance representing the transverse conduction current flowing between the two conductors of the line and Λ > 0 − the length of the line. For the system (1) can be formulated the following mixed problem: to find voltage u(x,t) and current i(x,t) along the line. From mathematical point of view this means to find two unknown functions u(x,t) and i(x,t) in П such that the following initial and boundary conditions be satisfied
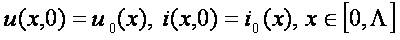
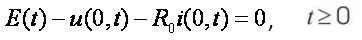
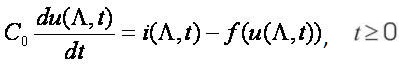
Here io(x),uo(x) are prescribed initial functions − the current and voltage at the initial instant.
The Kirchoff's law yields the boundary conditions. The V-I characteristic of the resistive load i=f(u) contains nonlinearities of exponential type (cf. below).
The reduction of the above mixed problem (cf. [3]) leads to the following neutral differential-difference equation on the right boundary:
where the unknown function is u(t) = u (Λ ,t) and
Here we consider (5) with exponential V-I characteristic of the nonlinear resistive element (cf. [4,5]) of the type:
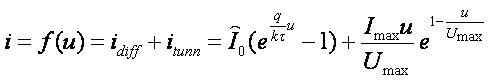
and using denotations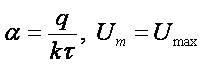 
we have
where Io,Im,α,Uo are prescribed positive constants.
Replacing (6) in (5) we obtain
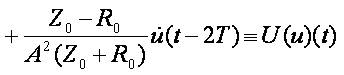
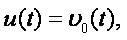
for 
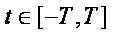
where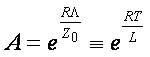 
Now we are able to formulate the main problem: to find an oscillatory solution of problem (7) with advanced prescribed zeros on an interval (to ,∞ ), to ≡T where vo(t) is a prescribed initial oscillating function on the interval [-T,T]. The initial function is obtained from the initial condition (2) by translation along the characteristics (cf. [2], [3] and references to them).
Let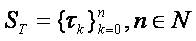 
be the set of zeros of the initial function, that is,υo (τk)= 0 such that τo = -T ,τn = T ≡ to. Besides
max{ τk+1 -τk:k =0,1,...,n-1} ≤ To
Let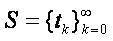 
be a strictly increasing sequence of real numbers satisfying the following conditions ( c):
(C1)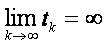 
(C2)for every k there is s
Remark 1.1 Condition (C2) implies
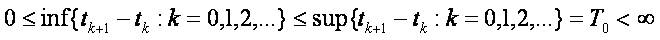
and
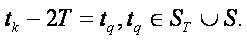
Introduce the set C1 [to,∞]consisting of all continuous and bounded differentiable functions with bounded derivatives on every interval[tk,tk+1] . We note the functions from C1 [to,∞] might not be differentiable at tk . More precisely the left and right derivatives might not coincide. That is why, we introduce below a topology of uniform convergence on every interval [tk, tk+1] which needs introducing of uniform spaces (cf. [6]).
Let us consider the sets
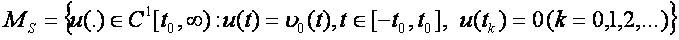
and
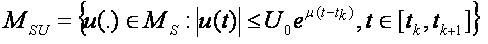
where Uo, µ are positive constants and µo =µTo=const.
Remark 1.2. The functions from MSU are not necessary differentiable at the points 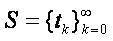which implies that we have to consider a space with countable family of pseudo-metrics, but not with one metric. Therefore we have to involve the fixed point theory in uniform spaces (cf. [6,7]).
Introduce the following family of pseudo-metrics
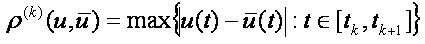
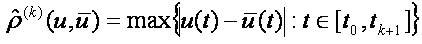
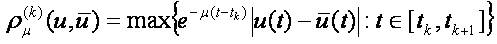
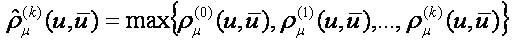
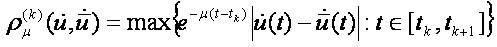
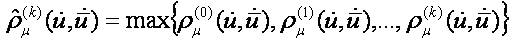
The following inequalities imply the equivalence of the both families of pseudo-metrics
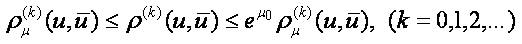
It is easy to verify that
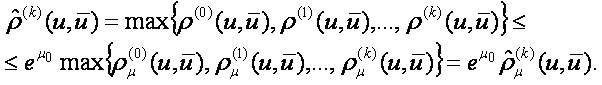
The set MSU turns out into a complete uniform space with respect to the family of pseudo-metrics
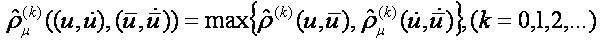
Define the operator B by the formulas
We introduce the following conditions:
,
,
,
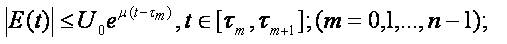
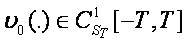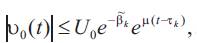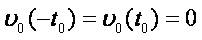
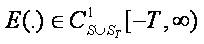such that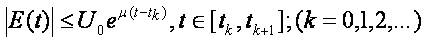
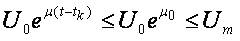
Denote by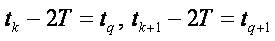 
where 
Lemma 1.1 Problem (1.7) has a solution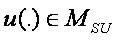 
iff the operator B has a fixed point in MSU , that is,
Proof: Let 
be a solution of (1.7). Then integrating (1.7) on every interval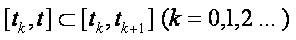 
we obtain
and then
Therefore u(t) satisfies
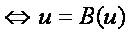
that is,u is a fixed point of B.
Conversely, let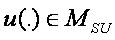 
be a fixed point of B (that is, solution of (2.2)) or
Prior to prove that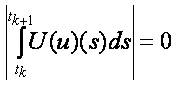 
we note that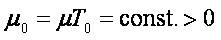 
,
and 
where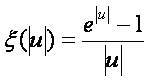 
is increasing. Therefore the condition 
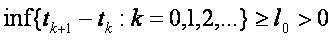is not necessary.
Since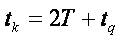 
,
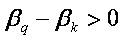and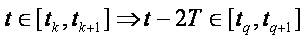 
It follows for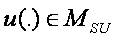 
that
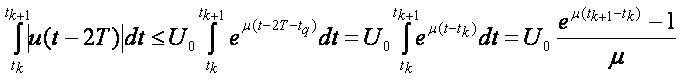
Therefore
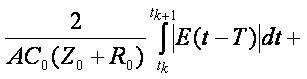
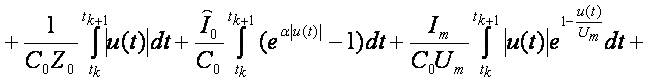
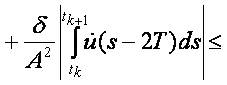
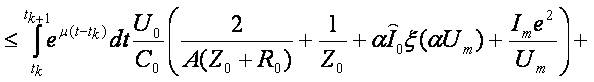
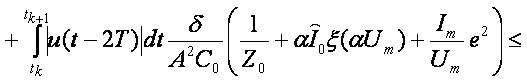
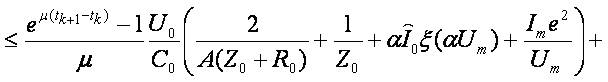
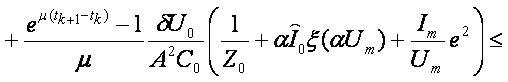
Obviously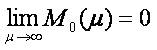 
and consequently 
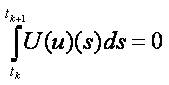. Then
Differentiating the last integral equation we obtain (1.7).
Lemma 1.1 is thus proved.
Theorem 1.1 Let the following conditions be fulfilled:
, 
,
;
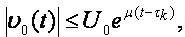
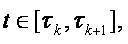
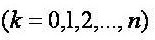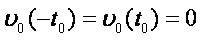
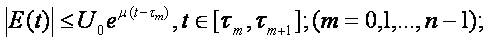Then there exists a unique oscillatory solution of the initial value problem (7) belonging to MSU .
Proof: They show that B maps MSU into itself, that is u ∈ MSU , implies B(u)∈ MSU
First we show that B(u)(t) is continuous on[to,∞] . Indeed,
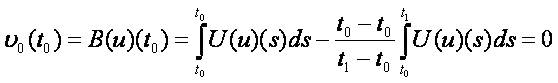
Besides B(u)(t) is differentiable on every [tk ,tk+1]
Next we show that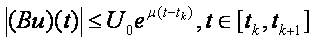
We notice that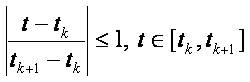
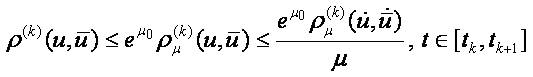
For every u(.)∈ MSU and sufficiently large µ we obtain
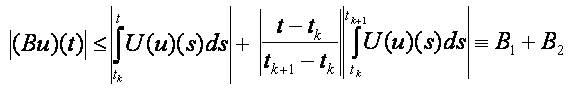
But
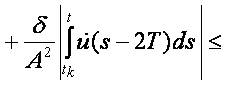
and
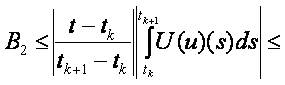
Therefore for sufficiently large µ > 0 and t ∈ [tk,tk+1]and we obtain
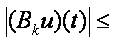
Consequently B maps MSU into itself.
It remains to show that B is a contractive operator. We make estimation on every interval [tk,tk+1]:
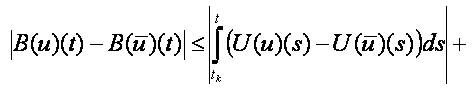
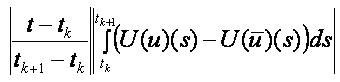
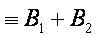
We notice that
Then for t∈ [tk,tk+1]
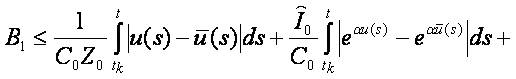
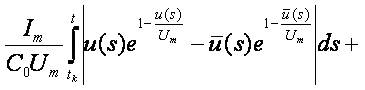
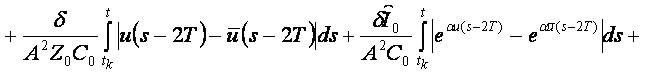
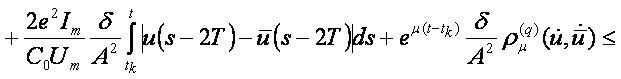
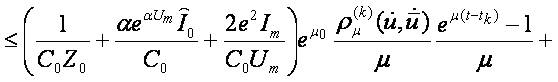
and
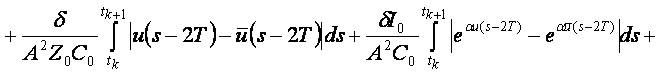
Consequently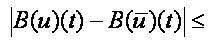
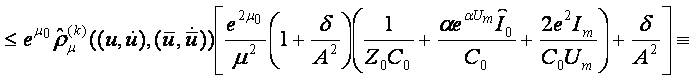
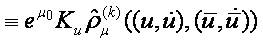
It follows
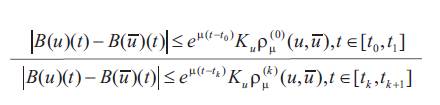
and then
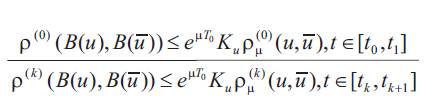
imply (in view of (2.1))
Therefore
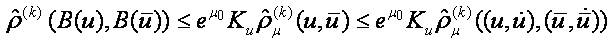
Obviously the Lipschitz constant does not depend on the index k of the family of pseudo-metrics.
For the derivative for t ∈ [tk,tk+1]we obtain:
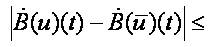
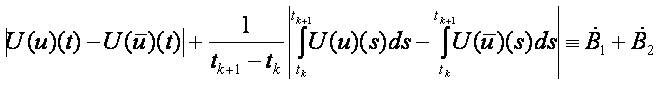
We have
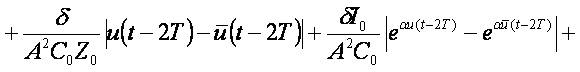
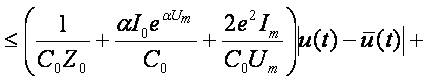
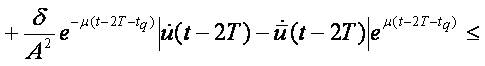
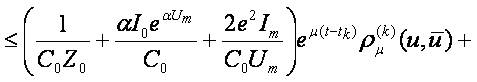
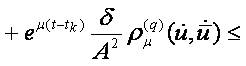
and
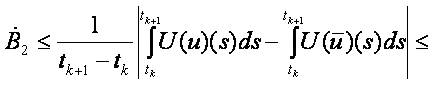
Then we obtain
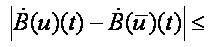
It follows
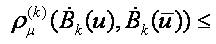
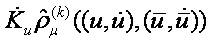
Therefore
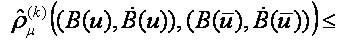
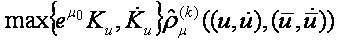
We have to verify that MSU is j-bounded. Indeed, since j is an identity mapping
Then in view of the fixed point theorem for contractive mappings in uniform spaces (cf. [6], [7]) operator B has a unique fixed point. The obtained fixed point is an oscillatory solution of (7).
Theorem 1.1 is thus proved.
We collect all inequalities implying the above theorem that could be applied to analysis of transmission lines:
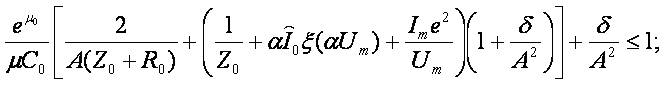
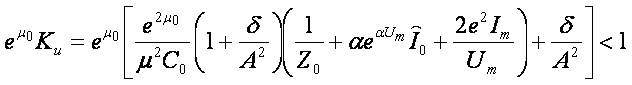
Consider a cuprum transmission line with length Λ = 1000 m,cross-section area S =10 mm2. Specific resistance for the cuprum is ρc =0,0175,, the resistance per-unit length is R=1,75 Ω. Let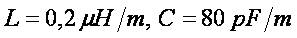 
. Then
,
,
,
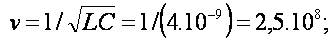
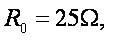
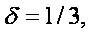
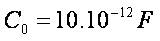
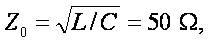
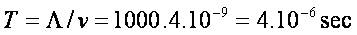
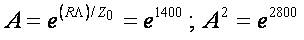
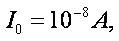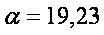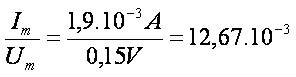
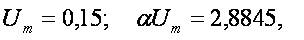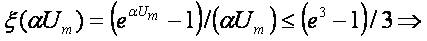
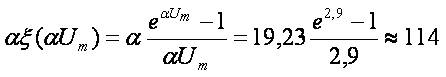
Let us check the propagation of waves with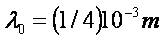 
Then
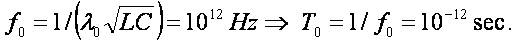
If we choose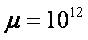 
then
,
,
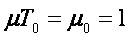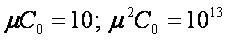Then the above inequalities become
; 
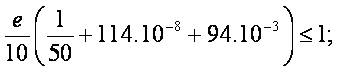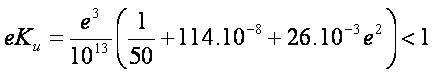
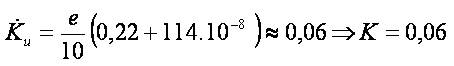
The rate of the convergence depends on K.
The main advantage of the presented method is its direct applicability. To verify the conditions for an existence-uniqueness of oscillatory solution is not necessary to read the proof of the theorem. It suffices to verify the inequality given in numerical example. Successive approximations can be obtained beginning with simple trigonometric functions. Let us point out the authors reach an explicit solution which is nonlinear function of sin and cos.