Numerical analysis is used to solve those algebraic and transcendental equations, which are difficult to solve by usual Mathematical methods. Methods like Bisection, Regula falsi and Newton-Raphson are generally used for this purpose (Gerald & Wheatley, 2004); (Hildebrand, 1982); (Ortega, Poole & Jr., 1981);( Kreyszig, 1972); (Sidi, 2006); (Terry, 1984). The various methods are discussed below.

Since the method is based on finding the root between two points. Here the root bracketed between two points, x_i and x_i+1 give the mid-point between them and generates two new intervals

1. x_i and x_m(i,i+1)

2. x_i+1 and x_m(i,i+1)

Thus, there can be two cases

 

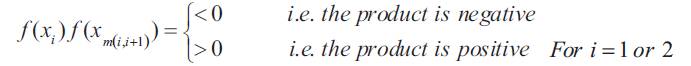
In the first case we say the root lies between x_i and x_m(i,i+1) whereas in second case the root lies between x_i+1 and x_m(i,i+1) .

This method is considered as the improvement of above stated method. Here, the process algorithm involve the following modified formula for x_m(i,i+1)

(1)

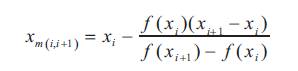
Bracketing of roots is made exactly in the same way as last method.

Both the above methods require the consideration of two points in each proceeding step. This method requires the input of single point. The formula defining its equation is as follows

(2)

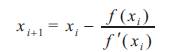
This method requires the computation of one derivative but its convergence is far better than Bisection and Regula falsi method. For this reason, among the discussed methods, Newton-Raphson is considered as best.

This method was originally proposed by (He, 2003). According to it,

(3)

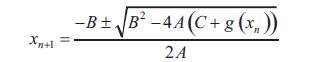
The evaluation of the claim and the complicacy in the result has been justified in Luo (2005).

The method has been developed by assuming the function f (X) to be continuous and differentiable within each point of its domain and at least in the part of domain in which the real root of the equation lie. The equation runs as follows,

(4)

The proposed method is an improvement to all these methods in terms of maintaining the precision of result and predicting the result with finer efficiency and accuracy.

The usual expectation from a mathematical method is to obtain the fast result by possibly minimum derivatives, particularly for the cases where the higher derivatives are difficult to obtain. Present work found these expectations through the use of Taylor's theorem; thereby obtaining an efficient and highly convergent method that not only works faster than conventional methods but also takes lesser iteration steps than those of recently proposed iterative methods say Hybrid iteration method (Luo, 2005),Method (He, 2003)), Maheshwari's method (Maheshwari, 2012).

Let the function defining the equation f (X) = 0 is continuous and differentiable in its domain and at least in the part of domain in which the real root of the equation lies. The present derivation moves on the line of Maheshwari's method (Maheshwari, 2012). So, let L (X_n , f (X_n )) and M (X₀ , f (X₀ )) are two points such that f (X ₀) and f (X_n ) are opposite in sign and the ordinate of the given equation f (X) = 0 follows the inequality | f (X₀ ) | < | f (X_n ) |. Clearly, the equation of the line LM will be,

(5)

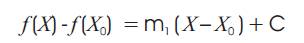
Where, C is the length of the intercept made by the line on Y – axis, and 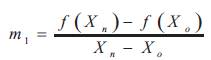represents the slope of the line. Let, a tangent is drawn through the point M. The slope bisector of the line containing L & M and the tangent at M is obtained.

The equation of this slope bisector will be,

(6)

(7)

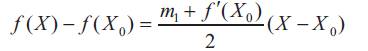
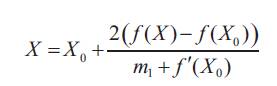
It passes through x-axis and meets it at the point “A”. The value of abscissa correspond to this point gives the initial approximation of the root of the given equation which comes out to be,

(8)

Substituting the value of m₁ and rewriting the expression in term of iteration step, we obtain

(9)

Again, by Taylor expansion of f (X) we have,

(10)

Where, is the nth approximation to the root of the equation f (X) = 0.

Let, X₀ be the root of equation f (X) = 0 in the open interval I, in which the function is continuous and has well defined first order  derivative. So,

(11)

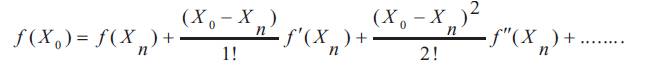
Using the fact f (X₀ ) = 0

(12)

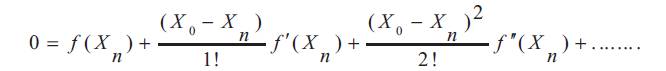
Considering only the linear terms of equation (12), the value of the root X₀ can be obtained,

(13)

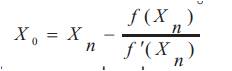
Equations (9) and (13) constitute the required iteration procedure to proceed through the fast convergence of the targeting model equations.

• Choose two points X_n1 and X_n2 such that f (X_n1 ) and f (X_n2 ) are opposite in sign. If f (X_n1 ) < f (X_n2 ), we take X_n = X_n1 , otherwise  vice-versa.
• Using equation (9) & equation (13) consecutively to obtain the approximation of the result by the proposed formula.
• The process is repeated to get the result from next iteration, which in turn will give more exact result.
• The process terminates when required level of accuracy is obtained.

Following illustrative example defines the result obtained by present method to solve targeting type of equations. At the same time, the results are compared with Newton's method and some other recent methods to compare the efficiency and accuracy of it.

Illustrative Example: Consider the following equation (Luo, 2005)

(14)

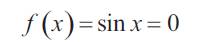
Taking X₀ = 1.5 as initial approximation. The results obtained by Newton iteration, hybrid iteration (Luo, 2005), result in (He,  2003) and present iteration method are shown in Tables 1-5. Table 1shows the Newton's iteration method for solving this  problem and the result of 3^rd iteration step is shown at n = 3. For the same problem, the hybrid iteration method is projected upto 17 steps in Table 2, but the level of accuracy is found to lesser than Newton's iteration method. Maheshwari's method in Table 3 shows the exact convergence at step 7. The result by present approach was also found in Table 4 and the satisfactory level of convergence has been obtained in 3^rd step. Capsulating all, the average error & efficiency of all the methods are compared in Table 5, which shows the remarkability of the present method over others.

Different results for the equation are shown in Tables 1-4. Here, represents the initial approximation of the root of the equation, is the iteration number made to obtain the final result and represents the value of absolute error at the nth iteration. It is apparent from these results that the present iterative formula is more effective than the other formulas of its class. The efficiency obtained in Table 5 for n = 3 shows that the present method is highly efficient in solving various targeted problems.

Table 1. Newton iteration (Luo, 2005) for solving f (x) = sinx = 0

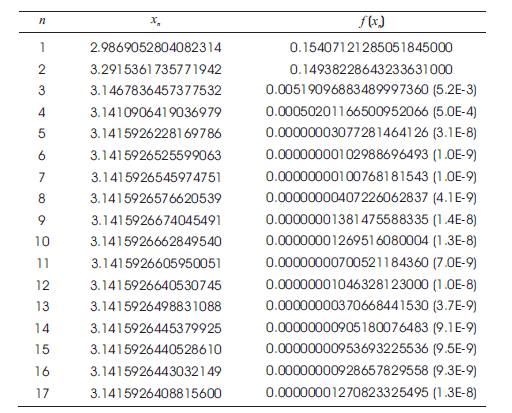
Table 2. Hybrid iteration (Luo, 2005), for solving f (x) = sinx = 0

Table 3. Maheshwari's method (Maheshwari, 2012) for solving f (x) = sinx = 0

Table 4. Present Approach, for solving f (x) = sinx = 0

Table 5. Average error & Efficiency η = 1/ε in all the formulas for n =3

Various observations can be made from the result drawn in the Tables. The main conclusions are as follows:

• Present method is a single derivative method that takes lesser number of iterations.
• Various results in the last column of the Tables show the absolute deviation in f(x). Here, it can be concluded that the value of absolute error is least in case of the present method.
• Efficiency analysis made in Table-5 for n = 3 shows that the present method is highly efficient in solving various problems of its class.