A fundamental assumption of teaching is that for learning to be generative, students and teachers must be engaged in learning that involves the same generative process that the teachers expect them to apply to use their knowledge to learn new ideas and solve unfamiliar problems in the future. The work of the central science projects illustrate how the instruction engages the students in generative activity. Students in these classes are regularly involved in constructing, testing, and revising models (Cartier & Stewart, 2000; Rosebery & Warren, 1998) and the students in both Science and Mathematics classes formulate and evaluate conjectures (Carpenter & Levi, 1999). A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the Natural Sciences and Engineering disciplines, as well as in the Social Sciences. Physicists, Engineers, Statisticians, Operations Research Analysts, and Economists use mathematical models most extensively. A model may help to explain a system and to study the effects of different components, and to make predictions about behaviour. The thing which I hear, I may forget. The thing which I see, I may remember. The thing which I do, I cannot forget (Naik, 1997). So the audiovisual aids and the models have an essential role in the development of the students understanding of Mathematics.

The study of numbers, equations, functions, geometric shapes and their relationships is called Mathematics. Some of its major subdivisions are arithmetic, algebra, geometry, and calculus (Dictionary.com, 2015). So also the systematic treatment of magnitude, relationships between figures and forms, and relations between quantities expressed symbolically. Mathematics is mental activity which consists in carrying out, one after the other; those mental constructions which are inductive and effective (Snapper, 1979). The letters of the word mathematics stands for Master, Accuracy, Talent, Hard work, Efficiency, Minuteness, Adventurous, Time management, Ideas, Confidence and Sensible or smartness.

Teaching is for learning, learning is for understanding, and understanding is for reasoning, applying and ultimately problem solving. In Mathematics teaching and learning is done by understanding the abstract concepts.

Abstraction in mathematics is the process of extracting the underlying essence of a mathematical concept, removing any dependence on real world objects with which it might originally have been connected, and generalizing it, so that it has wider applications or matching among other abstract descriptions of equivalent phenomena (Robert, 1998).

Teaching aids are materials that the classroom teacher uses to help the students to understand the concepts when she/he introduces the lessons. These teaching aids can take numerous forms. From pictures, students might learn how to count. While teaching Mathematics in kindergarten,teachers might display the photos of famous Mathematicians and places during a session on the history of Mathematics (Rickey, 2013). Teaching aid is any device, object, or machine used by a teacher to clarify or enliven a subject. Teaching aids are the materials or equipment used in teaching (Farlex, 2012).

4.1 Manipulatives

Manipulatives are tools which are used to make abstract concepts more real. These teaching aids helps children to understand Mathematics by looking at it from different views, according to Burns, 2005 founder of Mathematics Solutions. Manipulatives may include color tiles, pattern blocks, interlocking cubes and a variety of measuring tools, all of which the students can easily comprehend. One of the Common Core Standards of Mathematical Practice asks the teachers to model with mathematics. Teachers use manipulatives to achieve that goal. Burns recommends using manipulatives in all mathematics classes from kindergarten to high school.

4.2 Electronics and Media

Teachers uses interactive whiteboards, tablets and computers to stimulate their students and hold their attention with visuals. In the interactive whiteboard connects, the teachers use the computer and a projector, which can be used to show the lesson in one touch on the screen, to the entire class. The interactive lesson allows students to manipulate objects on the screen. They become participants in active learning, rather than spectators in a passive process.

4.3 Graphic Organizers

Graphic organizers are visual graphics that help and organize the students thinking and it can be used in any subject matter. The students can use them to organize their learning by constructing Venn diagrams, t-charts, story maps, flow charts and timelines. Once the students organize their ideas, they can spot trends and patterns in the concepts.

4.4 Audiovisual Aids

The term “audio-visual aids” is commonly misapplied. Any instructional device that can be heard as well as seen is called as audiovisual aids (Audible Films, Closed circuit Televisions). The aids themselves must have something either audible or visual, or both. The common types of audible aids are the spoken word, recognizable sound effects, and music. The most frequently used visual aids are pictures, cartoons, graphics, maps, the printed word, and three-dimensional models. When people talk about a motion picture projector or a blackboard, they are talking about the means of presenting the aids, and not the aids themselves (Kelley & Thomas, 1961). Audio-visual aids are those sensory objects or images which initiate or stimulate and reinforce learning.

The Mathematics teacher can prepare a video clip on the subject in mathematics (i.e, the history of mathematics or explain the concept of mathematics or Biography of Mathematicians) with a mix of audio. For instance Biography of Ramanujam, Area of the Circle, Explain the concept of Pythagoras theorem, etc. are some of the Audio- Visual Aids.

4.5 Auditory Aids

Every instructional device that is heard but not seen is called an audio aid. The examples for the audio devices are Tape records, Speakers, Earphones, etc. The learners gain knowledge of Mathematics by hearing the recorded classes, tables, formulas, etc, through an audio device.

4.6 Visual Aids

Several instructional devices that can be seen, but not heard are called visual aids. It is of two types

• Not requiring projection: eg. Chalkboard, Flannel graph, Exhibits, Posters, etc.
• Requiring Projection: eg. Slides, Film Strips, Epidiascopes, OHP (Over Head Projector), etc.

Learning takes place by the visual aids like derivation/explanation in a chart, formulae in a flashcard, geometrical figures in transparencies charts/sheets, relationships in tree charts, paper cuttings as posters, enlarging the mathematics concept by photographs of mathematicians in a book or printed material, through epidiascopes, giving visual to the transparencies sheets by over head projectors, etc.

Visual aids can be broadly divided into two types as given below based on their operation.

Projected visual aids are pictures shown upon a screen by use of a certain type of machine such as Motion Picture Projector, Filmstrip Projector, Opaque Projector, Overhead Projector, and Slide Projector.

Projected aids having the following advantages,

• Provides greater enjoyment in learning
• Stimulates more rapid learning
• Increases retention: larger percentages and longer retention
• Makes teaching situation adaptable to wider range
• Compels attention
• Enlarges or reduces actual size of objects
• Brings distant past and the present into the classroom
• Provides an easily reproduced record of an event
• Influences and changes attitudes

Motion picture projector will project a series of pictures from a strip of film in such rapid succession as to give the appearance of movement to objects. In Mathematics education, the motion picture projector is used to introduce the mathematical concept or explain the biography of mathematicians. The entire strips with series of mathematical concepts, through the projector each and every strip will be sequentially projected. The image of the motion picture projector is shown in Figure 1.

Figure 1. Motion Picture Projector

The Mathematics teachers use the filmstrip projector to project the film-strip with mathematical concept. The advance the projector uses a film of size 35 mm and displays one frame at a time and the image is shown in Figure 2.

Figure 2. Filmstrip Projector

Opaque projector is a device which displays opaque materials by shining a bright lamp onto the object from above. Opaque projector will project the image of any opaque material, either flat or three-dimensional, placed beneath its lens. Also it can project images of book pages, drawings, mineral specimens, leaves, etc. The image of the opaque projector is shown in Figure 3.

Figure 3. Opaque Projector

The overhead projector is preferred by the teachers for many reasons. It is easy to operate, projects a large, clear image, and, as was previously mentioned, there is no need to darken a room to use it. The projector also is designed so that the person using it faces the audience, making it possible to maintain easy eye contact at all times. If the teacher wishes to point out something on the screen, the speaker merely takes a pencil and touches it to the transparency, which lies face up and easily readable on the projection surface. The image of the pencil appears like a pointer on the screen behind them. Equipment projects the image contained on transparent slides up to 10" X 10". Each transparency must be positioned on the projector by hand. The word "overhead" is taken from the design of the equipment, which actually projects the image to a mirror held above the transparency, which in turn reflects it over the head of the speaker to the viewing surface (Yousra & Barkat, 2013). The Mathematics concepts are written in the transparencies sheet and placed above the glass in the over head projector. The image of Overhead Projector is shown in Figure 4.

Figure 4. Overhead Projector

Equipment projects the image contained on a small transparent slide, usually 35 mm. Many of these projectors are equipped with magazines to hold a large number of slides, and operation can be either manual or automatic. The Mathematics concepts was written in every slide and placed in required place in an orderly manner. The image of the slide projector is shown in Figure 5. There are two types of slides, they are Photographic slides (2” X 2”, 3” X 4”, Black and white, Colored) and Handmade slides (Acetate sheet, Cellophane, Etched glass). Slides can be made from photographs and pictures by teachers and pupils. The arrangement of slides in proper sequence, according to the topic discussed, is an important aspect of teaching with them.

Figure 5. Slide Projector

Non projected visuals are those aids which are used without any projection. So they translate abstract ideas into a more realistic format (Word Press, 2009). The non projected teaching aids allow instruction to move from verbal representation to a more concrete level (Audio aids / Graphic aids / Display boards / Activity aids). The non projected aids are listed below: Black board, Magnetic board, Photography board, Flannel board, Flip board, Bulletin board, Pocket board, Diagrams board, Graph board, Match board, Charts, Flash cards, Rotating disk, Match cards, Maps, Pictures, Posters, Cartoon, Graphs, Radio, Phonograph, Tape Recorder, etc.

The Non projected aids having the following Advantages,

• Abundant and are easily obtainable.
• Requires no electricity
• Appropriate for low budget
• Not much artistic ability is required in the use of these visual aids.
• Can be used in many ways at all levels of instruction and discipline
• Used to stimulate creative expression such as story telling or writing stories
• Many of them can be converted into projected aids.
• Some of them can be projected through an opaque projector.

4.7 Boards

Boards are useful to present or display a set of information in words, diagram, graph, combination of word graphs, and diagrams, etc. The boards are fixed or portable. The mathematics teacher uses the boards to draw or explain the mathematical concepts or problems, and also prepare a card to display in flannel board, flip board, bulletin board, etc. The explanation of various boards are given below in detail.

Wherever your learning takes place, blackboard provides the tools that elevate education for all in the classroom. In teaching Mathematics blackboard takes an important role to solve the problem and to draw the diagrams. The image of the blackboard is shown in Figure 6.

Figure 6. Black Board

Magnetic boards have revolutionized, the way in which information is relayed in offices, schools and even at home. Magnetic boards are less hazardous especially for the asthmatic people who easily get irritated by chalk dust. Magnetic boards were first used in classrooms where they replaced chalk boards. They are used by tutors for teaching purposes. A tutor writes on the white magnetic boards by using non-permanent ink pens. The information can be erased by using a magnetic eraser and more information can be written. They can also be used at home or in kindergartens to teach children how to construct letters or pictures. Using magnetic letters and patterns, a child can create different words, pictures or patterns on a magnetic board. Figure 7 shows the image of Magnetic Board.

Figure 7. Magnetic Board

Children explore mathematics concepts like shapes, pattern with colorful crayons and count up bugs. Each magnetic mathematics board comes with a set of starter magnets and corresponding picture magnets. Children simply stick the starter magnets in the left column of the board and then add picture magnets as they count from 1 to 20, sort objects by shape or extend simple patterns (Probst & Richards, 2013).

The Photography board which consists of pictorial materials, photos and information is still used for the educational purpose or any other needs. In mathematics it consists of photographs of mathematicians, image of mathematical models, mathematical pictures, etc. Figure 8 shows the image of Photography Board.

Figure 8. Photography Board

Flannel board is a thick board which is covered by flannel cloth. The children will easily find counting of flannel pieces as they are added to the board. Atleast two of each shape, size, and color are cut so that children can match items. These pieces can be geometric shapes, hearts, shamrocks and anything easy to cut from felt. The children are invited to sort/classify by colour, size, or shape. As their skills grow they will begin to classify by two attributes (colour and size), putting the large red shapes together and the small blue shapes in another place on the flannel board. The image of Flannel Board is shown in Figure 9.

Figure 9. Flannel Board

The flip board is used to teach the continuous concept like story, poem, etc. In mathematics, it is of help to teach the formulas, tables, etc. The image of the flip board is shown in Figure 10.

Figure 10. Flip Board

A bulletin board is a surface intended for the posting of public messages, for example, announce events or provide information. Bulletin boards are often made of a material such as cork to facilitate addition and removal of messages, or they can be placed on computer networks, so that people can leave and erase messages for other people to read and see. In mathematics classroom it is of help to exhibit the information for the students. Shapes, quotes of mathematicians, riddles, puzzles, magic squares, etc. are displayed in the bulletin board. Figure 11 shows the image of Bulletin Board.

Figure 11. Bulletin Board

Pocket board is the main teaching/learning tools. It consists of a large number of pockets in which “pocket cards” are inserted. Cards are made by thin cardboard. It consists of alphabets, words, images, numbers, and so on. These boards and cards are also used to construct words and sentences. The size of a pocket board is normally about 6 feet in length and 4 feet in width. The mathematics teacher uses the pocket board to introduce numbers, formulas and to check solution of the problem. Also it helps the learners to identify the mathematical concepts by themselves. The image for Pocket Board is shown in Figure 12.

Figure 12. Pocket Board

The background of the graph board was in the form of laminated graph sheet. The teacher can easily draw the graph in this laminated graph board while teaching. The graph in the graph board is easily understood by the learners. Figure 13 shows the image of Graph Board.

Figure 13. Graphs Board

Match board is the board prepared by the teacher to recall the content after the teaching. It consist of sets of information which is not in any order, and the learner makes them in order. The image for the match board is given in Figure 14.

Figure 14. Match Board

4.8 Charts

It is defined as combination of graphical and pictorial materials designed for the orderly and logical visualizing of relationships between mathematical key facts and ideas. There are several types of charts, they are narrative chart, tabulation chart, chain chart, bar chart, pie chart, flow chart, evolution chart, pull chart, line chart, tree chart and so on Figure 15 shows the image of Charts.

Figure 15. Charts

Flash cards are the series of stiff cards, which is usually small enough to be held in the hands, each of which is imprinted with one or more key words. Flash cards are small cards of generally 25×30 cm in size which are shown for a few moments before the class to send across a message or impart an idea. The image for Flash Cards is shown in Figure 16.

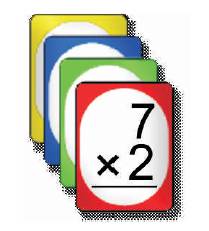
Figure 16. Flash Cards

Match cards are pieces of cards, which helps the learners to assemble them according to their nature. The learners classify the formulas, symbols, etc. in the match cards as learning equipment. The sample of the match card is given in Figure 17.

Figure 17. Match Cards

Pictorial materials are so easily available yet some teachers complain that they cannot get 'good' pictures for teaching purposes. These teachers seem to be confused with what constitutes a 'good' picture (Thapliyal, 2012). Actually, any picture in the hands of the skilful teacher can be effectively used for teaching purposes. In pictorial material the author included the following areas maps, pictures, posters, cartoon, graphs, etc. The sample of the Pictorial Materials is shown in Figure 18.

Figure 18. Pictorial Materials

The numbered rotating disc is a teaching aid for children which comprises a base, and is structurally characterized by a supporting rod arranged on the base, and a rotating disc in the front with operational signs and a rotating disc in the rear with numbered circular sheets at the edge are respectively fixed on the shaft. The image for the rotating disk is shown in Figure 19.

Figure 19. Rotating Disk

The phonograph, in its later forms also called a gramophone or record player, was a device introduced in 1877 for the mechanical recording and reproduction of sound. The sound vibration waveforms are recorded as corresponding physical deviations of a groove engraved or impressed into the surface of a rotating cylinder or disc. To recreate the sound, the surface is similarly rotated while a playback stylus traces the groove and is therefore vibrated by it, very faintly reproducing the recorded sound. In early acoustic phonographs, the stylus vibrated a diaphragm which produced sound waves which were coupled to the open air through a flaring horn, or directly to the listener's ears through stethoscope-type earphones. In later electric phonographs, the motions of the stylus are converted into an analogous electrical signal by a transducer called a pickup or cartridge, then electronically amplified, and later converted back into sound by a loudspeaker (Newville, 1959). It is the traditional technological aid to play back the excellent talk of mathematicians or about mathematicians. The image of phonograph is given in the Figure 20.

Figure 20. Phonograph

An audio tape recorder or tape deck or tape machine is an audio storage device that records and plays back sounds, including articulated voices, usually using magnetic tape, either wound on a reel or in a cassette, for storage. In its present day form, it records a fluctuating signal by moving the tape across a tape head that polarizes the magnetic domains in the tape in proportion to the audio signal. Tape-recording devices include reel-to-reel tape deck and the cassette deck. Radio and tape recorder are used to record or play the sound effects, and music. It is useful to record an excellent mathematician's talk and play back in the classrooms. The image of tape recorder is shown in Figure 21.

Figure 21. Tape Recorder

A mathematical model is an abstract model that uses mathematical language to describe the behaviour of a system. Mathematical models can take many forms, including but not limited to dynamical systems, statistical models, differential equations, or game theoretic models. These and other types of models can overlap, with a given model involving a variety of abstract structures. In general, mathematical models may include logical models, as far as logic is taken to be a part of mathematics (Bender, 2000). The two types of models are working models and non working models. Working model is a small object, usually built to represents the aspects of another large object to explain in the classroom with motion (working). Non working model is also the representation of large object with all aspects as model (building, tower, etc.).

Teachers use computers or the Internet for instructional purposes related to their training, preparation and work environments. Teachers are more likely to use these technologies when the technologies are available to them in their classrooms as opposed to computer labs, and available in greater numbers. It helps the mathematics teacher to provide a concrete effect for some abstract concept. Also it helps to teach effectively, actively, efficiently, successfully, enthusiastically, dynamically, resourcefully, productively and creatively.

Good teaching aids should be meaningful and purposeful, accurate in every aspect, simple, cheap, improvised as for as possible, large enough to be properly seen by the students for whom they are meant, up-to-date, easily portable, in accordance with the mental level of the students, and should motivate the learners.

In teaching Mathematics, it is important to implement appropriate techniques and teaching aids. The teacher is responsible for choosing the best techniques and methods that will give opportunity to the learners to gain knowledge as much as possible. Selecting the way of teaching Mathematics is based on the class situation and on the learners' condition. The teaching aids for Mathematics which are discussed in this paper is very essential in the classroom for the progress in learning to understand the concept. Today people are living in a rich and sophisticated audio visual environment. The teachers, must rise up to the reality that this radically changes their pupils' expectations.