Several researchers including Krishna B. Misra [1], Dekker et.al. [2], Wang, H Z[3] and Rizwan &Gulshan[4] have contributed to this challenging area of reliability of systems and have given pathways to meet the real challenges in industries as far as its real application is concerned.The effectiveness of any system depends on its reliability which keeps the system performance close to the original expectations. Systems in practice are subject to deterioration with usage and age. In order to keep those deteriorated systems useful in terms of its extensive quality lifetime and reducing the cost of operations and preventing the occurrence of system failures, regular monitoring, repairs and replacements are necessary. Maintenance models provide the basis of any maintenance quantitative analysis in terms of reliability indices which in turn are helpful in evaluating the overall system performances.

Referring[1] & [4], if the authors consider that the system has only two possible states: working state and failure state which applies to the components of the system as well, then the reliability indices for the system is evaluated as follows:

Availability is the probability of finding the component / device / system in the operating state at some time into the future. There are several kinds of availability indices. For example:

• Point availability: A (t) =P {the system is in a working state at time t}.
• Steady State availability:

if the limit exists, average availability over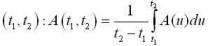

and Limit average availability: 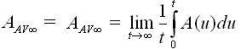if the limit exists.

Reliability is the capacity of parts or components or units, and systems to perform their required functions for desired periods of time without failure in a specified environment and with a desired confidence. Several indices have been used to describe the system reliability related performance. For example,

Repairable system reliability: R (t) =P {the system never fails before time t}.
Mean time to system failure (MTSF)

How many repairmen or devices can be used to repair a repairable system? In general, the following indices are used:

{the repairmen or devices are busy, at time t}, if the limit exists.

• Point wise probability of repair facility for being busy: B(t) =P{the repair facility is busy at time t}
• Steady-state busy probability of repairman:
• Mean Time To Repair (MTTR):The total amount of time spent performing all corrective maintenance repairs divided by the total number of those repairs.

This reflects the frequency of failures or replacements occurring in the repairable system, which can be depicted by the following indices:

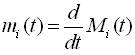• Point wise failure frequency: and
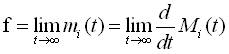• Steady-state failure frequency: if the limit exists;

where N(t) is the number of failures of the system occurring in the time interval and {X(t),t ≥ 0} is a stochastic process describing the repairable system.

This reflects the number of visits of the repairman who comes to repair/replace the failed unit(s) and repair all the units which fail during his stay at the system. In steady state, the expected number of visits per unit time is 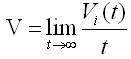, if the limit exists; where V_i(t) is the cumulative number of visits up to time t.

The models being discussed could be fine-tuned for analyzing a multi- unit system/plant of domestic waste water treatment plant. The waste water treatment plants to treat domestic waste water uses biological process for treatment out of which activated sludge processes are in common. This treatment plant consists of several units like: collection well, screening chambers, initial settling tank, aeration tanks, secondary clarifier, filtration and chlorination, to treat the waste water. There are several pumps of different capacity and mechanical equipment that are used to facilitate treatment. It is not unusual that, many of the treatment plants work at more than the peak load due to seasonal variations and unpredicted population increase. The challenge with the operator is to manage and meet the effluent quality after the treatment when it is disposed or used for irrigation purpose. Hence it recommended for studying the nature of failure and recasting such situations for better operation, reliability and performance of such units. Referring[5] ; is a case analysis of a waste water treatment plant. The plant operates at a minimum capacity during the non-touristic months and at full capacity during touristic months which is roughly for about 6 months in a year. The main components of the plant are pumps used for pumping at various stages. The pumps for pumping from the primary settling tank for pretreatment are of 6 in nos. with a capacity of 168cu. m. /hr. where one is always kept as standby pump. There are 4 pumps for supply of ferric chloride, which work at intervals and 5 pumps used for back washing and to pump out the treated effluent. The reliability of these pumps/components is useful from maintenance perspective in order to carry on the whole process without the component failures of tolerable limits and there is no alternative way as well to store the waste water other than treating the effluents and rejecting to the sea. It is observed that the plant is failing due to two reasons as categorized viz., minor or major. However, the variation into the modeling could be analyzed by introducing the concept of inspection for detecting the type of failure. Three years of maintenance data for this treatment plant have been considered and important reliability indices are obtained. The semi-Markov process and regenerative point techniques are used in the entire analysis.

Using the data as in [5] along with some assumed values to match with realistic failure situations of the plant and introducing the inspection rate (α), the following values of rates and various costs are estimated along with some assumptions:

• Estimated rate of failure of any component of the unit (λ) = 0.00134 per hour
• Estimated rate of the unit moving from peak to off peak season (β) =0.000114 per hour
• Estimated rate of Maintenance (Y) = 0.000232 per hour
• Probability of occurrence of Minor failure (p₁) = 0.8462
• Probability of occurrence of Major failure (p₂) = 0.1231
• Estimated value of repair rate of Minor repairs (α₁) = 0.08351 per hour
• Estimated value of repair rate of major repairs (α₂) = 0.029701per hour
• i(t)= αe^-αt where α is the inspection rate = 0.04 per hour

λ: Failure rate of units
i(t): probability density function of inspection
p₁ : Probability of occurrence of minor failure
p₂ : Probability of occurrence of major failure
β: Rate of shutting down of 3 pumps during off peak season
©: Convolution between the distributions
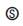: Steiltje's convolutionbetween the distributions
r: Rate of recovery after shut down during peak season
g₁(t), G₁(t): probability density function(pdf) and cumulative distribution function(cdf) of minor repair
g₂(t), G₂(t) : pdf and cdf of major repair rate
Φ_i(t): cdf of first passage time from a regenerative state i to a failed state j

• There are six pumps in the plant, of which 5 operate at any given time and one pump is always kept as standby.
• An inspection is carried out to identify the type of failure (minor / major)
• Maintenance of no pump is done if the repair of some other pump is going on.
• The plant goes for annual maintenance during off peak season for six months and works on reduced capacity with 3 pumps working.
• If a unit is failed in one season, it gets repaired in that season only.
• Not more than two pumps get failed at a time.
• During the maintenance of one pump, more than one of the other pumps cannot get failed.
• All failure times are assumed to have exponential distribution with failure rate λ, whereas the repair times have general distributions.

The indices, in this case, are mean time to plant failure and plant availability. There are many other indices as mentioned in the above sections, which are equally important in order to get a better estimation of Profit.

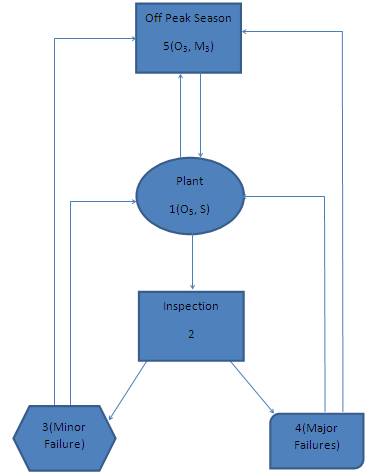
Figure 1. State transition diagram

This could be a very effective mathematical tool to solve the real time problems from maintenance perspective once they understand the system/plant behavior through estimated reliability indices.

A state transition diagram shows the possible states of transition of the plant as shown in Figure 1. The epochs of entry into states 1, 2, 3, 4 and 5 are regeneration points and hence these states are regenerative states. The transition probabilities are given by:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

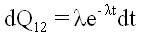
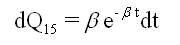
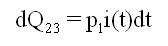
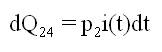
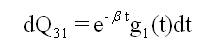
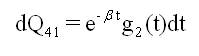
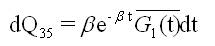
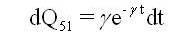
By these transition probabilities it can be verified that

(10)

(11)

(12)

(13)

(14)

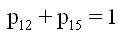
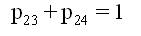
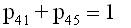
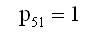
The mean sojourn time (µ_i) in the regenerative state 'i' is defined as the time of stay in that state before transition to any other state. If T denotes the sojourn time in the regenerative state 'I', then:

(15)

(16)

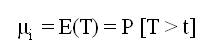
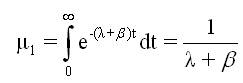
Similarly, it could be for states 2, 3 and 4 also.

The unconditional mean time taken by the system to transit for any regenerative state 'j' when it (time) is counted from the epoch of entrance into state 'i' is mathematically stated as:

(17)

The unconditional mean time taken by the system from different states could be evaluated using the above formula.

3.1 Mean Time to System Failure

Regarding the failed states as absorbing states and employing the arguments used for regenerative processes, the following recursive relation for Φ_i(t) is obtained:

(18)

(19)

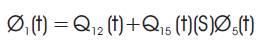
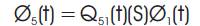
Now the mean time to plant failure when the unit started at the beginning of state 1, is given by

(20)

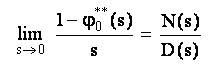
Solving for Φ₀**(s) by taking Laplace Stieltje's transforms, the Mean Time to System Failure (MTSF) when the unit started at the beginning of state 0, is

(21)

3.2 Availability Analysis of the Plant

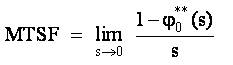
Using the probabilistic arguments and defining A(t) as the probability of plant entering into upstate at instant t, given that the unit entered in regenerative state i at t=0, the following recursive relations are obtained:

(22)

(23)

(24)

(25)

(26)

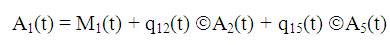
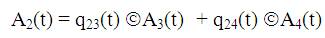
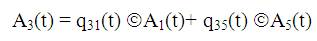
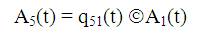
Where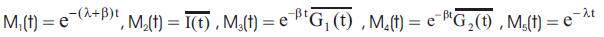

Taking Laplace Transforms of the above equations and solving them for A₀*(s), we get

(27)

The steady state availability is given by:

(28)

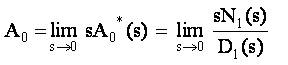
Similarly, the recursive relations for other indices could be obtained and by solving them using determinant methods, we can estimate their numerical values.

For this particaular case, all failure rates are exponentially distributed whereas other rates are general. Using the data summary and the expressions of reliability indices, various measures of system effectiveness are estimated as follows

Mean time for the system failure = 746hours
Availability of the system = 0.996790084
Expected busy period for repair = 0.0020380

Similarly, many other reliability measures of the plant such as expected number of minor repairs, expected number of major repairs, expected number of replacements, expected number of minor replacements and the expected number of major replacements could be obtained.

Reliability modeling and analysis proves to be an effective mathematical tool for analyzing effective maintenance practices in any complex system. Given a risk factor, the model predicts the breakdown and repair possibilities and offers a scientific basis on which the optimum reliability results are achieved. In the present analysis, it is worth noting that by introducing inspection, an improved value of MTSF (746 hours) could be obtained as compared to what has been achieved by Rizwan et.al. [5] (429 hours). Slight improvements are noted in other indices as well.