Proximal positive Parallel Notation: A Novel Method Of Expressing Mathematical Complements, Collaborations, And Combinations
Abstract
This monograph provides anepistemological rational for the mathematical “Proximal Positive Parallel Notation” as a novel mathematical operation. This innovative mathematical notation is used to define the relationship between values that construct the Standard Tri–Squared Test 3 × 3 Table used in the transformative process of qualitative data into quantitative outcomes. The Tri–Squared Test was introduced in an earlier Journal on Mathematics article by the author. The mathematical notion of “Unlimitation” is also introduced as an explicative part of the definition of the Proximal Positive Parallel formulae. Integrated into this new parallel notation is the neoteric “Coextensive” sign as a symbol of the relationship between terms. The Proximal Positive Parallel as a unique and inventive mathematical notation that may be applied to other areas and arenas of mathematics, statistics, and other sciences. Its broader application in diverse academic fields (such as the social sciences) will aid in building and strengthening the connections between mathematics and other academic disciplines.
Keywords :
- Bijection,
- Categorical,
- Coextensive,
- Collaboration,
- Combinations,
- Complements,
- Coordinate,
- Equinumerosity,
- Equation,
- Exponent,
- Formula
- Instrument,
- Integer,
- Investigation,
- Mathematical Model,
- Mathematics,
- Notation
- Parallel,
- Positive,
- Proximal,
- Reflexivity
- Research,
- Statistics,
- Symmetry,
- Table,
- Triangulation,
- Trichotomy,
- Tri–Squared,
- United,
- Unlimited,
- and Universal
Introduction
The field of mathematics has a great number of ideas, conventions, and rules all aimed at the expression of complex and detailed concepts in a concise, simple, and succinct form. This process is referred to as mathematical “parsimony”. Parsimony is the ability to express much in a few words. The use of the principle of parsimony leads to the expression of mathematical concepts in equations and formulate that is referred to mathematicians as “mathematical beauty”. Great mathematicians such as Euler and Gauss are both credited with parsimonious use of Greek capital letters to indicate summation in a series (via Sigma: Σ) and multiplication in a series (via Pi: Π) respectively. It is in the same vein as the aforementioned mathematical pioneers, that the author offers the “Proximal Positive Parallel Notation” and its subsequent nomenclature as a novel mathematical operation.
1. The Structure, Notation, and Nomenclature of Sequential Mathematical Operations
Mathematical operations in a sequential series have a unique pattern that is commonly used across each specific operation. Mathematical Summation in a Series is called “Summation Notation”and has a unique structure and mathematical nomenclature that is of the following form:
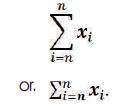
Mathematical Multiplication in a Series is called “Product Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
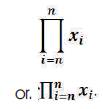
Mathematical Categorical Summation in a Series is called “Coproduct (Co–product) Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
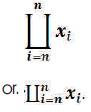
Mathematical Union of Sets in a Series is called “Union Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
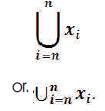
Mathematical Intersection of Sets in a Series is called “Intersection Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
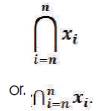
Mathematical Vector Summation in a Series is called “Vector Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
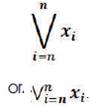
Mathematical Wedge Product of Vectors in a Series is called “Exterior Product Notation” and has a unique structure and mathematical nomenclature that follows pattern of Summation Notation and has the following form:
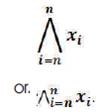
Historically the “Proximal Positive Parallel Notation” is property and an abstraction drawn out of the “Total Transitive Tandem of Visualus” first introduced in the book Visualus written by the author in 2010. The “Proximal Positive Parallel Notation” nomenclature follows the aforementioned mathematical conventions and is of the following form: 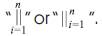 This particular method of mathematical writing and transforming the traditional mathematical parallel sign or symbol of “||” into the form
This particular method of mathematical writing and transforming the traditional mathematical parallel sign or symbol of “||” into the form 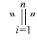 is called “Proximal Pairing”. The “Proximal Pairing” in terms of coordinates relates to the positive values in the first quadrant of the Cartesian Coordinate graph (values that are integers and are [positive, positive] in regards to the Cartesian Coordinate abscissa [x] and ordinate [y]). The Proximal Pairing in this case becomes the symbol for the “Proximal Positive Parallel”. It is now mathematically defined as the positive parallel of a set of Cartesian Coordinates that is multiplicatively balanced in a one–to–one ratio that is equally and directly proportionate (meaning the values of the Proximal Positive Parallel are equally matched and what is done to one value must be correspondingly done to its partner).
is called “Proximal Pairing”. The “Proximal Pairing” in terms of coordinates relates to the positive values in the first quadrant of the Cartesian Coordinate graph (values that are integers and are [positive, positive] in regards to the Cartesian Coordinate abscissa [x] and ordinate [y]). The Proximal Pairing in this case becomes the symbol for the “Proximal Positive Parallel”. It is now mathematically defined as the positive parallel of a set of Cartesian Coordinates that is multiplicatively balanced in a one–to–one ratio that is equally and directly proportionate (meaning the values of the Proximal Positive Parallel are equally matched and what is done to one value must be correspondingly done to its partner).
Proximal Positive Parallel Notation has a set of values that immediately follows the 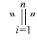 and uses the
and uses the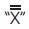 sign.The
sign.The 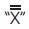 sign is called the “Coextensive” and it indicates the one–to–one correspondence between the Proximal Positive Parallel Notation values. The coextensive sign is mathematically defined as the “Complementally Collaborative Combination” of the values that follow the Proximal Positive Parallel nomenclature.
sign is called the “Coextensive” and it indicates the one–to–one correspondence between the Proximal Positive Parallel Notation values. The coextensive sign is mathematically defined as the “Complementally Collaborative Combination” of the values that follow the Proximal Positive Parallel nomenclature.
2. Application of the Proximal Positive Parallel Notation in Proximal Positive Parallel Mathematical Models
The Proximal Positive Parallel Notation Square Exponent Equation:
In this case,  is defined as the “complementary, collaborative, combination of [x1...n ] and [y1...n ]”, indicating that the square of the given set of Cartesian Coordinates are thereby equal as specified in the following mathematical form: [x21....n ] = [y 21...n].
is defined as the “complementary, collaborative, combination of [x1...n ] and [y1...n ]”, indicating that the square of the given set of Cartesian Coordinates are thereby equal as specified in the following mathematical form: [x21....n ] = [y 21...n].
Where,

and

for
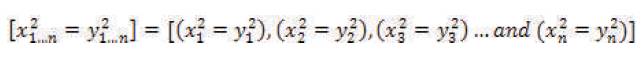
Thus,
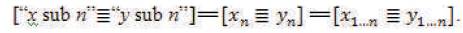
Note: is defined as,“Cartesian Coordinate x sub n is [“strictly equivalent to”]Cartesian Coordinate y sub n”.
is defined as,“Cartesian Coordinate x sub n is [“strictly equivalent to”]Cartesian Coordinate y sub n”.
Therefore, the complete mathematical definition equation for the “Extended Proximal Positive Parallel Notation Square Exponent Equation”(that explains the coextensive complementary collaborative combination of Cartesian Coordinates) is of the following form:
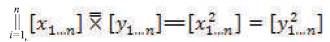
The Proximal Positive Parallel is mathematically defined as follows:
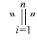 =Proximal Positive Parallel Notation, where, “||”═ the “Proximal Parallel Pairing”, i ═ the “index” and n ═ the highestnumber value for the indicated Cartesian Coordinates in subscripts.
=Proximal Positive Parallel Notation, where, “||”═ the “Proximal Parallel Pairing”, i ═ the “index” and n ═ the highestnumber value for the indicated Cartesian Coordinates in subscripts.
3. The Mathematical Definition of the Proximal Positive Parallel Notation
The mathematical definition of the Proximal Positive Parallel Notation: The Parallel symbol [“||”] is associated with the geometric principle of “Parallel Lines”. The Parallel symbol is a signal that the idea of two or more ideas, terms, concepts, and/or integers are strictly equivalent to 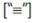 and parallel to each other. The “Index of Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Parallel values. The “Lower Limit of Parallel” indicates the smallest value the index will take on. In this example, the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Proximal Positive Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates:
and parallel to each other. The “Index of Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Parallel values. The “Lower Limit of Parallel” indicates the smallest value the index will take on. In this example, the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Proximal Positive Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates:
[x1...n ] = The Cartesian Coordinate “x” from point 1 to “n”;
[y1...n ] = The Cartesian Coordinate “y” from point 1 to “n”;
[x21..n ] = The Cartesian Coordinate “x” Squared ═ [x2 ]═ “x⋅x” from point 1 to “n”;
[y21...n ] = The Cartesian Coordinate “y” Squared ═ [y2] ═ “y⋅y” from point 1 to “n”;
[x1...n|| y1...n ]═[xn y n] ═ The Parallel Cartesian Coordinates x and y, where, xn ||y n(“x subscript n is parallel to y subscript n for all subscript n, meaning n must be strictly equivalent to n”). As a result, n ═ n, thus, xy (“x⋅y”) has the property of “n parallel equality”, this leads to parallel [x⋅y] or ||xn yn with n ═ n;
x⋅y═[xy] ═ The multiplication of Cartesian Coordinates “x” and “y”;
x 1...ny1...n ═ [xn yn] ═ The multiplication of Parallel Cartesian Coordinates “x” and “y” indicated by subscripts [1…n] and [n];
[x21...n ] ═ [x2n ] ═ The square of Cartesian Coordinate x;
[y21...n ] ═ [y2n ] ═ The square of Cartesian Coordinate y; and
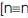 =[n ═ n]═ The parallelism [“||”] and strict equality
=[n ═ n]═ The parallelism [“||”] and strict equality 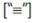 and equality [“═”] for all subscript values of n.
and equality [“═”] for all subscript values of n.
The mathematical formula for the extended definition of the Proximal Positive Parallel Notation Square Exponent Equation is mathematically written as:
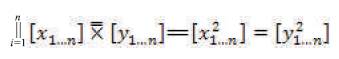
“The Proximal Parallel Positive of i to n for the concentration of all x sub 1 to n times y sub 1 to n is equal to the parallel of the concentrated square of x sub 1 to n equal to y sub 1 to n”. It is important to note that: “What happens to coordinate x must equally happen to coordinate y.”
The Parallel Square Exponent Equation has the following mathematical properties:
1) Parallelism: is indicated by the Parallel symbol “||”. This mathematical property has the following geometrical mathematical definition — Two lines that never connect but are essentially the same.In Euclidean geometry a line is not considered to be parallel to itself (Coxeter, 1961), but in affine geometry it is convenient to hold a line as parallel to itself, thus yielding parallelism as an equivalence relation (Szmielew, 1983).
2) Positive Integers: The term “Integer” derives from the Latin word “Integer” which literally means “untouched” or “whole” and from the French word “entire” (the word entire comes from the same origin, but via French) (Evans, 1995). A Positive Integer is a number that can be written without a fractional or decimal component. The numbers 1, 2, and 3 are examples of Positive Integers; 3.50, 3½, and 3 are not integers. The set of Positive Integers is a subset of the real numbers, and consists of positive whole natural numbers (0, 1, 2, 3...).
3) Bijection: In mathematics, a bijection or bijective function is a one–to–one correspondence (Wolf, 1998). It is a mathematical function that gives an exact pairing of the elements of two sets. Every element of one bijective set is paired with exactly one element of the other bijective set, and every element of the other set is paired with exactly one element of the first set. Thus, there are no unpaired elements. In formal mathematical terms, a bijective function is written f: X → Y and is defined as a one–to–one pairing and mapping onto each element of a set X to each element of a set Y. It is important to note that the bijection from the set X to the set Y has an inverse function that is written is written f: Y → X. If X and Y are finite sets as in the Proximal Positive Parallel Notation Square Exponent Equation, then the existence of a bijection means they have the same number of elements. A bijective function from a set to itself is also called a “permutation”. In mathematics, in the Proximal Positive Parallel Notation Square Exponent Equation the permutation refers to the listing of the Cartesian Coordinates x and y positive integers as a sequential discrete set of objects arranged into a particular order (0, 1, 2, 3...).
4) Equinumerosity: Equinumerous finite sets have the same number of elements. Equinumerosity has the characteristic properties of an equivalence relation (Suppes, 1972). An equivalence relation partitions (or divides into parts) a set so that every element of the set is a member of one and only one cell of the partition (as each member of the set of Tri–Squared outcome values is a member of only one cell of the 3 by 3 Tri–Squared Table). Equinumerosity in the mathematical Proximal Positive Parallel Square Exponent Equation, applies to the two sets A (associated with the Cartesian Coordinate x) and B (associated with the Cartesian Coordinate y) are said to be “Equinumerous”. This is true because there is a one–to–one correspondence (a Bijection) between each Coordinate of x with each Coordinate of y. The Equinumerous function for the Proximal Positive Parallel Notation Square Exponent Equation from A to B such that for every element y of B there is exactly one element x of A is f(x) =y. In the Proximal Positive Parallel Notation Square Exponent Equation all Cartesian Coordinate x and y values are Positive Integers that have Equinumerosity (“equalness–of–number”), Equipollence (“equalness–of–strength”), and Equipotence (“equalness–of–power”). The statement that the two Proximal Positive Parallel Notation Square Exponent Equation sets A and B are Equinumerous is denoted as follows:
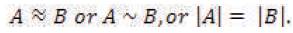
Equinumerosity also has three distinct characteristic properties of an equivalence relation: Reflexivity, Symmetry, and Transitivity. They are defined as follows:
Reflexivity: In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself. In other words, a relation ~ on a set S is reflexive when x ~ x holds true for every x in S (Levy, 1979).Given the Cartesian Coordinate x as set A, the identity function on set A is a Bijection from set A to itself, showing that every set A is Equinumerous to itself. This is mathematically written as: A ~ A.
Symmetry: Symmetry here refers directly to “Symmetry Group” as a part of the Bijection property and is Equinumerous. The symmetric group on a set of n elements has order n! (Jacobson, 2009).For every Bijection between the two Cartesian Coordinates x and y represented as sets A and B respectively, there exists a mathematical inverse function which is a Bijection between B and A. This implies that if a set A is Equinumerous to a set B then B is also Equinumerous to set A. This is mathematically written as: A ~ B and implies that B ~ A.
Transitivity: According to the Encyclopedic Dictionary of Mathematics from the Massachusetts Institute of Technology (MIT Press) 2000 [The Encyclopedic Dictionary of Mathematics is a translation of the Japanese Iwanami SugakuJiten (岩波数学辞 典) authored by ShokichiIyanaga in several revisions and updated editions dating from 1954, 1960, 1968, 1977, 1980, and 1985], the formal definition of Transitivity in terms of a binary relation R is usually defined as an ordered triple (X, Y, G) where X and Y are arbitrary sets (or classes), and G is a subset of the Cartesian product X × Y. The sets X and Y are called the domain (or the set of departure) and codomain (or the set of destination), respectively, of the relation, and G is called its graph. The statement (x,y) ∈ R is read “x is R–related to y”, and is denoted by xRy or R(x,y). The latter notation corresponds to viewing R as the characteristic function on X × Y for the set of pairs of G. The order of the elements in each pair of G is important: if a ≠ b, then aRb and bRa can be true or false, independently of each other. Resuming the above example, the prime 3 divides the integer 9, but 9 doesn't divide 3. A relation as defined by the triple (X, Y, G) is sometimes referred to as a correspondence instead. In this case, the relation from X to Y is the subset G of X × Y, and "from X to Y" must always be either specified or implied by the context when referring to the relation. In practice correspondence and relation tend to be used interchangeably (Iyanaga, 1977 and MIT Press, 2000).In terms of the, given three Cartesian Coordinates x, y, and z represented as sets A, B and C respectively, there are two Bijections f: A → B and g: B → C that are reflective of the three sets. Therefore the composition of these Bijections is gof (a mathematically written statement that means the set g is composed with the set f). The statement “gof” is a Bijection from set A to set C, so that if sets A and B are Equinumerous and sets B and C are Equinumerous then it follows transitively that sets A and C are Equinumerous as well. This is mathematically written as: A ~ B and B ~ C and together they both imply that A ~ C.
5) 1st Quadrant (+, +) Cartesian Coordinates: 1st Quadrant (positive, positive) Cartesian Coordinates are a planar coordinate system of graphing that specifically identifies each point on a uniquely gridded plane by a pair of numerical coordinates, which are the assigned distances from the point which is the direct intersection of two fixed perpendicular lines (that are generally measured by the same unit of length). Each line is called a Cartesian coordinate "axis" of the system, and are assigned a specific name (the positive horizontal line to the right being identified as “x” = the “abscissa” and the positive vertical line up being identified as “y” the ordinate). The point where x and y meet is referred to as the “origin”, usually at the ordered pair (0, 0). The Cartesian Coordinates are positions of space that are the perpendicular projections of a point on two axes, that is expressed as assigned distances from the point of origin identified as (0, 0).
6) Graphic Square Exponentiation: “The Graphic Square Exponent” or “Graphing Squared Exponentiation” in terms of Cartesian Coordinates for the Eduscience statistical analytical model Tri–Squared is best explained by two mathematical concepts one is traditional the other is novel. The first traditional mathematical concept is that of logarithms and the novel mathematical concept is that of “Unlimitation” or the “Unlimit” of a set of values. A Logarithm is another mathematical method of expressing exponents. The Logarithm of a given number is the exponent to which fixed value, called "the base", must be raised to produce that number. Thus, for x2, x is considered the base and “2” is the exponent that raises the base (to “x⋅x”). The term “Logarithm” literally means “ratio–number” and was created by mathematician John Napier who derived it from the combination of the Greek word “Logos” meaning “Proportion, Ratio or Word” and the term “Arithmos” meaning “number”. The “Graphic Square Exponent Logarithm” is of the form: loga(y) = 2 which is equal to [a2=y]. The novel mathematical concept is that of “United Universal Unlimitation”. The mathematical principle of “Unlimit” written as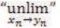 is represented as the “United Universal Unlimitation” identifies a value that is analogous to another value and adjoins that value by being near or in close proximity to it. The concept of the United Universal Unlimit was created by the author based on the mathematical idea of the “limit” but differs in its oppositional meaning, direct application, and in its written form. The notion of Unlimit implies “no limit” or “infinite possibility”. The “Unlimited” or principle of “Unlimitation” is used here to explain the strict equality and close proximity of perpendicular Cartesian Coordinates (via subscripts) that are multiplied to square a value and are parallel, directly proportionate, and directly equal but are on diverse lines (the abscissa and the ordinate respectively). The notation of “Unlimit” as the “United Universal Unlimited…” in terms of Tri–Coordinates (abscissa [x–coordinate], ordinate [y–coordinate], and applicate [z–coordinate]) Proximal Positive Parallel Notation is expressed as follows:
is represented as the “United Universal Unlimitation” identifies a value that is analogous to another value and adjoins that value by being near or in close proximity to it. The concept of the United Universal Unlimit was created by the author based on the mathematical idea of the “limit” but differs in its oppositional meaning, direct application, and in its written form. The notion of Unlimit implies “no limit” or “infinite possibility”. The “Unlimited” or principle of “Unlimitation” is used here to explain the strict equality and close proximity of perpendicular Cartesian Coordinates (via subscripts) that are multiplied to square a value and are parallel, directly proportionate, and directly equal but are on diverse lines (the abscissa and the ordinate respectively). The notation of “Unlimit” as the “United Universal Unlimited…” in terms of Tri–Coordinates (abscissa [x–coordinate], ordinate [y–coordinate], and applicate [z–coordinate]) Proximal Positive Parallel Notation is expressed as follows:

[Note: The notation above and below the coordinate indicates the possible magnitude and direction of vector for that particular coordinate in space from point of origin (0, 0).] =

Where, “The Unlimit of Positive Cartesian Coordinate x to y to z” has multiple Tri–Coordinate values equal to and expressed as, “The Unlimited [Positive] Coordinates x to y to z that are the Parallel of n to n for the combination of the norms of vectors x with y with z.” This equation can be modified into the “Graphic Square Unlimit”. The Graphic Square Unlimit is of the form:  and is defined as 'The Unlimit of a sub n as 1 sub n corresponds to 1 sub n…n (or an increase beyond sub n)”. This equation literally means, “x sub one (or x1) is unlimitedly parallel to y sub one (or y1) and can be multiplied by it (x1⋅y1) to determine the precise number of the square on the 1st Quadrant of the Cartesian Coordinate plane (in this case is increased by a factor of one and is equal to one)”. Thus, the second level of Cartesian Coordinate Graphic Square Exponentiation would be(x2.y2 ), according to the Graphic Square Unlimit) and from here on up all Cartesian Coordinate values are Squared x2 is parallel and equal to y2 and both x2 and y2are mathematically parallel and are graphically perpendicular and are equal to a value 4, which is the precise number of squares on the Cartesian Coordinate 1st Quadrant graph before the lines for x2and y2 intersect). Thus x2 and y2 are increased by a factor of 2.
and is defined as 'The Unlimit of a sub n as 1 sub n corresponds to 1 sub n…n (or an increase beyond sub n)”. This equation literally means, “x sub one (or x1) is unlimitedly parallel to y sub one (or y1) and can be multiplied by it (x1⋅y1) to determine the precise number of the square on the 1st Quadrant of the Cartesian Coordinate plane (in this case is increased by a factor of one and is equal to one)”. Thus, the second level of Cartesian Coordinate Graphic Square Exponentiation would be(x2.y2 ), according to the Graphic Square Unlimit) and from here on up all Cartesian Coordinate values are Squared x2 is parallel and equal to y2 and both x2 and y2are mathematically parallel and are graphically perpendicular and are equal to a value 4, which is the precise number of squares on the Cartesian Coordinate 1st Quadrant graph before the lines for x2and y2 intersect). Thus x2 and y2 are increased by a factor of 2.
7) Absolute Value (or Modulus): In mathematics, the Absolute Value (or Modulus) is written as |x|. The |x| of a real number (any number along a continuous line) denoted as “x”. The real number “x” as the absolute value has the following mathematical properties:(a.) The absolute value of a number is the non–negative value of “x” without regard to its sign; (b.) The absolute value of the number is written |x| = x, this is true for a positive x, thus, |−x| = x is true for a negative x, and the absolute value of zero is written |0| = 0; (c.) The absolute value of the number 3 is 3, thus |3| = 3, and the absolute value of the number −3 is 3 and is written |−3| = 3; and(d.) The absolute value of a number may be thought of as its distance from zero (on the positive Cartesian Coordinate Line). Some authors use the terms “Valuation”, “Norm”, or “Magnitude” instead of “Absolute Value”. However, the word “norm” usually refers to a specific kind of absolute value on a field (which is also applied to other vector spaces) (Koblitz, 1984). In the Proximal Positive Parallel Notation Square Exponent Equation all positive Cartesian Coordinates are integers that have the Absolute Values |x| = x and |y | = y.
4. Clarifying the Unique Characteristics of the Proximal Positive Parallel Notation
The mathematical equation for the Proximal Positive Parallel Square Exponent Equation is written in the following manner:

The equation above literally means, “The Proximal Parallel Positive of i to 1 for the concentration of all x sub 1 to n that is the complementary, collaborative, combination of y sub 1 to n is equal to the parallel of the concentrated square of x sub 1 to n equal to y sub 1 to n”. As stated earlier it is important to note that: “What happens to coordinate x must equally happen to coordinate y in this equation.”
Each of the individual elements of the aforementioned equation has unique properties and can be parsimoniously defined in more detail. Thus, the elements of the presented equation are individually mathematically defined as follows:
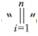 = Parallel Notation, where, “||”= the “Parallel”, i= the “index” and n= the highest number for the indicated Cartesian Coordinates. Mathematical Definition: The Parallel symbol [“||”] is associated with the geometric principle of “Parallel Lines”. The Parallel symbol is a signal that the idea of two or more ideas, terms, concepts, and/or integers are strictly equivalent to
= Parallel Notation, where, “||”= the “Parallel”, i= the “index” and n= the highest number for the indicated Cartesian Coordinates. Mathematical Definition: The Parallel symbol [“||”] is associated with the geometric principle of “Parallel Lines”. The Parallel symbol is a signal that the idea of two or more ideas, terms, concepts, and/or integers are strictly equivalent to 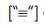 and parallel to each other. The “Index of Proximal Positive Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Proximal Positive Parallel values. The “Lower Limit of Proximal Positive Parallel” indicates the smallest value the index will take on. In this example the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn ] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates;
and parallel to each other. The “Index of Proximal Positive Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Proximal Positive Parallel values. The “Lower Limit of Proximal Positive Parallel” indicates the smallest value the index will take on. In this example the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn ] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates;
[x1...n ] = The Cartesian Coordinate “x” from point 1 to “n”;
[y1...n ] = The Cartesian Coordinate “y” from point 1 to “n”;
[x 21...n] = The Cartesian Coordinate “x” Squared ═ [x2 ]═ “x⋅x” from point 1 to “n”;
[y21...n ] = The Cartesian Coordinate “y” Squared ═ [y 2] ═ “y⋅y” from point 1 to “n”;
[x1...n || y1...n] ═ [xn || yn] ═ The Parallel Cartesian Coordinates x and y, where, xn ||yn (“x subscript n is parallel to y subscript n for all subscript n, meaning n must be strictly equivalent to n”). As a result, n=n, thus, xy (“x⋅y”) has the property of “n parallel equality”, this leads to parallel [x⋅y] or ||xn yn with n=n;
[x1...ny] ═ [xy] ═ The multiplication of Cartesian Coordinates “x” and “y”;
[x 1...ny1...n ] ═ [x y ] ═ The multiplication of Parallel Cartesian Coordinates “x” and “y” indicated by subscripts [1…n] and [n];
[x21...n ] ═ [x2n] ═ The square of Cartesian Coordinate x;
[y21...n ] ═ [y21...n ] ═ The square of Cartesian Coordinate y; and
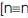 ═ [n ═ n]═ The parallelism [“||”] and strict equality
═ [n ═ n]═ The parallelism [“||”] and strict equality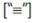 and equality [“=”] for all subscript values of n.
and equality [“=”] for all subscript values of n.
The aforementioned mathematical formula leads to the mathematical Parallel Square Exponent Equation for the Tri–Squared Statistic in the following manner:
5. Clarifying the Tri–Squared StatisticProximal Positive ParallelNotation Mathematical Model
The aforementioned Proximal Positive Parallel Notation Equation for Cartesian Coordinates x and y is a comprehensive mathematical formula that ultimately leads to the mathematical Proximal Positive Parallel Notation Square Exponent Equation for the Tri–Squared Statistic. This direct application of the Proximal Positive Parallel Notation Equation to the Tri – Squared Statistic is referred to as “Tri–Squared Proximal Positive Parallel Notation”. It is written in the following manner:
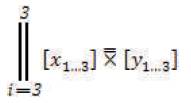
The definition for this mathematical model is, “The Proximal Parallel Positive of i to 3 with a total value of 3 Cartesian Coordinates for the concentration of all x sub 1 to 3 that is the complementary, collaborative, combination of y sub 1 to 3”. Definitively the Tri–Squared Proximal Positive Parallel Notation for the Tri–Square Bi–Coordinate Tri–Value Exponent Equation can be mathematically distinctively-defined in the following manner:
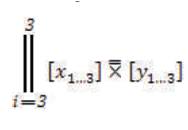
Where,
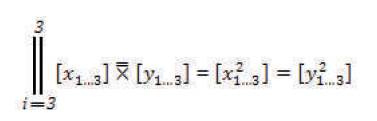
This in turn yields the following:

Consequently, the following is also true:
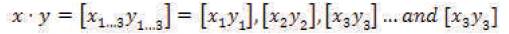
This can be further mathematically defined in the following sequential series of equations:
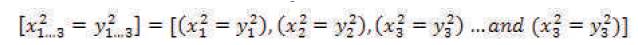
Therefore, the following lemma is true:
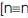 = [x = 3] ≡ [y = 3], because maximum value of n is three, thusly, n = 3.
= [x = 3] ≡ [y = 3], because maximum value of n is three, thusly, n = 3.
6. Applying Proximal Positive Parallel Notation the Visual Tri–Square Exponential Mathematical Models
The Proximal Positive Parallel Notation Model of the Tri–Squared Rectangular Parallel Bi–Coordinates [x] and [y] (that has the same exponents as the Proximal Positive Parallel Notation Square Exponent Bi–Coordinates) are ideally expressed in a sequential series of Cartesian Coordinate models. The Proximal Positive Parallel Square Exponent for the Bi–Coordinates [x] and [y] in a One–to–One Correspondence Model:
Note: In the lexicon of Tri–Squared mathematics the Model above has one–to–one Bi–Coordinates (meaning that each x coordinate is parallel to each y coordinate) with a parallel paired factorization that increases with a one–to–one ratio, thus, as x(the abscissa) increases y(the ordinate) has a corresponding equal value that increases exponentially(via squaring) at the same rate.
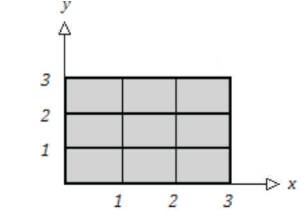
The Foundational Principles of Triangulation Exponentiation: The Parallel Square Exponent Bi–Coordinates [x] and [y] Isometric Rectangular Model:
Note: The Model above has the same one to one Bi–Coordinates with a rectangular factorization that increases with a one to one coordinate ratio.Thus, as x increases y also increases at the same rate as illustrated in the aforementioned Proximal Positive Parallel Notation Model.The Parallel Square Exponent Bi–Coordinates [x] and [y] Model illustrates this one–to–one Cartesian Coordinate proportion.[Note: The Model is rectangular in shape due to the dual triangulation of the Algorithmic Triangulation Model that makes up each Tri–Squared Table Cell].
Conclusion
The final mathematical form of the Tri–Squared Rectangular Proximal Positive Parallel Notation of Bi–Coordinates [x] and [y] is the United Universal Unlimited Positive Proximal Positive Parallel of the Tri–Squared Equation that creates the Standard 3 × 3 Tri–Squared Table which has the following mathematical form and definition:
The complete mathematical formula for the Tri–Squared Proximal Positive Parallel Square Exponent Equation is mathematically defined as:
Note: The shaded area indicates and illustrates the Standard 3 by 3 Table Tri–Squared Triangulation Table cell structure. In addition, the values that are outcomes of the Tri–Squared research investigation are “not limited” or are “Unlimited” in their range of possible values.
This series of sequential equations is defined as follows:
“In the book Visualus, the Proximal Positive Parallel is a property of “The Total Transitive Tandem”(Osler, 2010) and has a United Universal Unlimited endpoint of 3 that approaches 3 for the Tri–Squared Cartesian Coordinates x and y[that increases by a factor of 3 and are mathematically squared (32= 9)], thereby, creating the 3 by 3 Tri–Squared Table”.
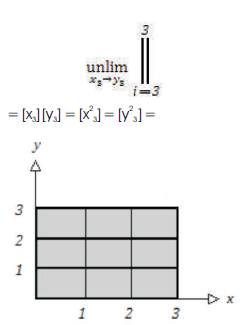
The Literal meaning of the Tri–Squared Proximal Positive Parallel Square Exponent Equation is defined, expressed, and modeled as follows:
“The United Universal Unlimit of [x sub 3] to [y sub 3] is exemplified by the Proximal Positive Parallel of 3 to 3 for the Cartesian Coordinate of [x sub 3] times the Cartesian Coordinate of [y sub 3] which is also equal to [x sub 3 squared] equal to [y sub 3 squared] that is the Tri–Squared 3 by 3 Table.”
This is ideally expressed sequentially in the following equation and associated Tri–Squared Visual Cartesian Coordinate Model:
Where, the above mentioned model has the following properties:
[x3][y3] = 9, [x 23] = 9, and [y23] = 9, as a result, [x3 ][y3] =[x23 ] =[y23] = 9, because, [x3][y3] = [x3⋅y3] = [x3y3] = 9 = the number of cells in the 3 by 3 Standard Tri–Squared Table = the number of rectangles derived from the Tri–Squared Equation, Trixy =[Trix • Triy ] =[3x • 3y ] =[3x • 3y]= 9xy. Thus, Trixy= 9xy.
This is due to the unique mathematical properties of United Universal Unlimited Positive Proximal Positive Parallel of the Tri–Squared Equation which has the following three mathematical conditions to be true:
- The Parallel Cartesian Coordinate x (which is x=x3= 3 from the abscissa) =3(3) =32= 9;
- The Parallel Cartesian Coordinate y (which is y=y3 = 3 from the ordinate) =3(3) =32= 9; and
- The Standard 3 by 3 Tri–Squared [Tri2 ] Table has9 “Microcotrines” (Osler, 2013a)that are the cells of the Tri–Squared Table and are of the tabular modular form:
This model is a 3 by 3 Tabular Rectangular Sequence of Microcotrines (Osler, 2013a). This means that a single “Rectangular Microcotrine 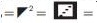 x y , and x is raised by y sequentially up to and no higher than 3, thus x2 = x3 = 9 and in parallel a single “Microcotrine”
x y , and x is raised by y sequentially up to and no higher than 3, thus x2 = x3 = 9 and in parallel a single “Microcotrine”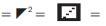 y x , and y is raised by x sequentially up to and no higher than 3, thus y3 = 32= 9 (Osler, 2013b). This is indicated by the shaded area on the aforementioned model of the Tri–Squared Proximal Positive Parallel of Square Exponent Equation graphs.
y x , and y is raised by x sequentially up to and no higher than 3, thus y3 = 32= 9 (Osler, 2013b). This is indicated by the shaded area on the aforementioned model of the Tri–Squared Proximal Positive Parallel of Square Exponent Equation graphs.
Summary
This unique mathematical notation may be applied to other areas and arenas of mathematics, statistics, and other sciences. The Positive Proximal Positive Parallel Notation defines the infrastructure of the Tri–Squared Standard 3 by 3 Table that is used to calculate the statistical Tri–Squared Test Equation.
References
[1]. Coxeter, H. S. M. (1961). Introduction to Geometry.John Wiley & Sons.p. 192. Encyclopedic Dictionary of Mathematics Volumes I–VI.(2000). MIT Press.pp. 1330–1331.
[2]. Evans, N. (1995). “A–Quantifiers and Scope”. In Bach, Emmon W. Quantification in Natural Languages. Dordrecht, The Netherlands; Boston, MA: Kluwer Academic Publishers. p. 262.
[3]. Iyanaga, S. (1977). Encyclopedic dictionary of mathematics, Volumes I, II, hardback, translated from the 2nd Japanese edition (1st ed.), MIT Press, pp. 1–1750.
[4]. Jacobson, N. (2009). Basic Algebra 1 (2nd ed.), Dover.
[5]. Koblitz, Neal (1984). P–adic numbers, p–adic analysis, and zeta–functions (2nd ed.). New York: Springer–Verlag.p. 1.
[6]. Levy, A. (1979). Basic Set Theory, Perspectives in Mathematical Logic, Springer–Verlag. Reprinted in 2002, by Dover.
[7]. Osler, J. E. (2010). Visualus ™ © Visioneering Volumetrically: The Mathematics of the Innovative Problem–Solving Model of Inventive Instructional Design (First Edition).Lulu Publishing, Morrisville NC.
[8]. Osler, J. E. (2013a). Algorithmic Triangulation Metrics for Innovative Data Transformation: Defining the Application Process of the Tri–Squared Test. April–June Journal on Mathematics,2 (2), pp. 10–16.
[9]. Osler, J. E. (2013b). The Triangulation Algorithmic: A Transformative Function for Designing and Deploying Effective Educational Technology Assessment Instruments. April–June Journal of Educational Technology,10 (1), pp. 46–54.
[10]. Suppes, P. (1972). Axiomatic Set Theory. Dover. Originally published by D. van Nostrand Company in 1960.
[11]. Szmielew, W.(1983). From Affine to Euclidean Geometry.Springer, p. 17.
[12]. Wolf, R. S. (1998). Proof, Logic and Conjecture: A Mathematician's Toolbox. W. H. Freeman.
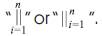 This particular method of mathematical writing and transforming the traditional mathematical parallel sign or symbol of “||” into the form
This particular method of mathematical writing and transforming the traditional mathematical parallel sign or symbol of “||” into the form 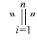 is called “Proximal Pairing”. The “Proximal Pairing” in terms of coordinates relates to the positive values in the first quadrant of the Cartesian Coordinate graph (values that are integers and are [positive, positive] in regards to the Cartesian Coordinate abscissa [x] and ordinate [y]). The Proximal Pairing in this case becomes the symbol for the “Proximal Positive Parallel”. It is now mathematically defined as the positive parallel of a set of Cartesian Coordinates that is multiplicatively balanced in a one–to–one ratio that is equally and directly proportionate (meaning the values of the Proximal Positive Parallel are equally matched and what is done to one value must be correspondingly done to its partner).
is called “Proximal Pairing”. The “Proximal Pairing” in terms of coordinates relates to the positive values in the first quadrant of the Cartesian Coordinate graph (values that are integers and are [positive, positive] in regards to the Cartesian Coordinate abscissa [x] and ordinate [y]). The Proximal Pairing in this case becomes the symbol for the “Proximal Positive Parallel”. It is now mathematically defined as the positive parallel of a set of Cartesian Coordinates that is multiplicatively balanced in a one–to–one ratio that is equally and directly proportionate (meaning the values of the Proximal Positive Parallel are equally matched and what is done to one value must be correspondingly done to its partner).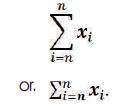
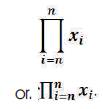
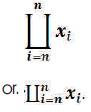
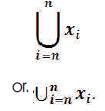
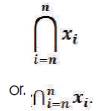
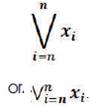
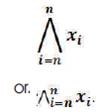
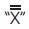 sign.The
sign.The 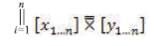
 is defined as the “complementary, collaborative, combination of [x1...n ] and [y1...n ]”, indicating that the square of the given set of Cartesian Coordinates are thereby equal as specified in the following mathematical form: [x21....n ] = [y 21...n].
is defined as the “complementary, collaborative, combination of [x1...n ] and [y1...n ]”, indicating that the square of the given set of Cartesian Coordinates are thereby equal as specified in the following mathematical form: [x21....n ] = [y 21...n].

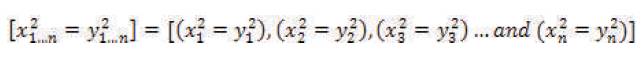
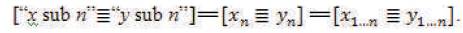
 is defined as,“Cartesian Coordinate x sub n is [“strictly equivalent to”]Cartesian Coordinate y sub n”.
is defined as,“Cartesian Coordinate x sub n is [“strictly equivalent to”]Cartesian Coordinate y sub n”.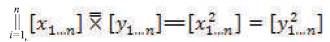
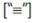 and parallel to each other. The “Index of Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Parallel values. The “Lower Limit of Parallel” indicates the smallest value the index will take on. In this example, the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Proximal Positive Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates:
and parallel to each other. The “Index of Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Parallel values. The “Lower Limit of Parallel” indicates the smallest value the index will take on. In this example, the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Proximal Positive Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates: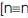 =[n ═ n]═ The parallelism [“||”] and strict equality
=[n ═ n]═ The parallelism [“||”] and strict equality 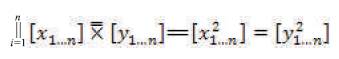
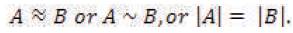
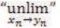 is represented as the “United Universal Unlimitation” identifies a value that is analogous to another value and adjoins that value by being near or in close proximity to it. The concept of the United Universal Unlimit was created by the author based on the mathematical idea of the “limit” but differs in its oppositional meaning, direct application, and in its written form. The notion of Unlimit implies “no limit” or “infinite possibility”. The “Unlimited” or principle of “Unlimitation” is used here to explain the strict equality and close proximity of perpendicular Cartesian Coordinates (via subscripts) that are multiplied to square a value and are parallel, directly proportionate, and directly equal but are on diverse lines (the abscissa and the ordinate respectively). The notation of “Unlimit” as the “United Universal Unlimited…” in terms of Tri–Coordinates (abscissa [x–coordinate], ordinate [y–coordinate], and applicate [z–coordinate]) Proximal Positive Parallel Notation is expressed as follows:
is represented as the “United Universal Unlimitation” identifies a value that is analogous to another value and adjoins that value by being near or in close proximity to it. The concept of the United Universal Unlimit was created by the author based on the mathematical idea of the “limit” but differs in its oppositional meaning, direct application, and in its written form. The notion of Unlimit implies “no limit” or “infinite possibility”. The “Unlimited” or principle of “Unlimitation” is used here to explain the strict equality and close proximity of perpendicular Cartesian Coordinates (via subscripts) that are multiplied to square a value and are parallel, directly proportionate, and directly equal but are on diverse lines (the abscissa and the ordinate respectively). The notation of “Unlimit” as the “United Universal Unlimited…” in terms of Tri–Coordinates (abscissa [x–coordinate], ordinate [y–coordinate], and applicate [z–coordinate]) Proximal Positive Parallel Notation is expressed as follows:

 and is defined as 'The Unlimit of a sub n as 1 sub n corresponds to 1 sub n…n (or an increase beyond sub n)”. This equation literally means, “x sub one (or x1) is unlimitedly parallel to y sub one (or y1) and can be multiplied by it (x1⋅y1) to determine the precise number of the square on the 1st Quadrant of the Cartesian Coordinate plane (in this case is increased by a factor of one and is equal to one)”. Thus, the second level of Cartesian Coordinate Graphic Square Exponentiation would be(x2.y2 ), according to the Graphic Square Unlimit) and from here on up all Cartesian Coordinate values are Squared x2 is parallel and equal to y2 and both x2 and y2are mathematically parallel and are graphically perpendicular and are equal to a value 4, which is the precise number of squares on the Cartesian Coordinate 1st Quadrant graph before the lines for x2and y2 intersect). Thus x2 and y2 are increased by a factor of 2.
and is defined as 'The Unlimit of a sub n as 1 sub n corresponds to 1 sub n…n (or an increase beyond sub n)”. This equation literally means, “x sub one (or x1) is unlimitedly parallel to y sub one (or y1) and can be multiplied by it (x1⋅y1) to determine the precise number of the square on the 1st Quadrant of the Cartesian Coordinate plane (in this case is increased by a factor of one and is equal to one)”. Thus, the second level of Cartesian Coordinate Graphic Square Exponentiation would be(x2.y2 ), according to the Graphic Square Unlimit) and from here on up all Cartesian Coordinate values are Squared x2 is parallel and equal to y2 and both x2 and y2are mathematically parallel and are graphically perpendicular and are equal to a value 4, which is the precise number of squares on the Cartesian Coordinate 1st Quadrant graph before the lines for x2and y2 intersect). Thus x2 and y2 are increased by a factor of 2.
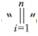 = Parallel Notation, where, “||”= the “Parallel”, i= the “index” and n= the highest number for the indicated Cartesian Coordinates. Mathematical Definition: The Parallel symbol [“||”] is associated with the geometric principle of “Parallel Lines”. The Parallel symbol is a signal that the idea of two or more ideas, terms, concepts, and/or integers are strictly equivalent to
= Parallel Notation, where, “||”= the “Parallel”, i= the “index” and n= the highest number for the indicated Cartesian Coordinates. Mathematical Definition: The Parallel symbol [“||”] is associated with the geometric principle of “Parallel Lines”. The Parallel symbol is a signal that the idea of two or more ideas, terms, concepts, and/or integers are strictly equivalent to 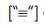 and parallel to each other. The “Index of Proximal Positive Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Proximal Positive Parallel values. The “Lower Limit of Proximal Positive Parallel” indicates the smallest value the index will take on. In this example the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn ] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates;
and parallel to each other. The “Index of Proximal Positive Parallel”, is the letter “i”, it is an ideal variable whose value indicates the starting point of the Proximal Positive Parallel values. The “Lower Limit of Proximal Positive Parallel” indicates the smallest value the index will take on. In this example the starting value of i is 1. Unless indicated otherwise, we increase this value by 1 until we reach the upper limit of Parallel. The “Upper Limit of Parallel” [n] indicates the largest value that ends the Parallel series. The expression to the immediate right of the Parallel describes or represents each individual parallel value and its relationship to other value that are parallel to it, starting with the index variable “i”. Parallel Notation is ideally used to describe Bi–Coordinate Cartesian Coordinate subscripts [xn and yn ] that are used to identify the mathematics of squaring in terms of Cartesian Coordinates;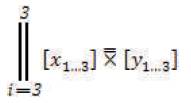
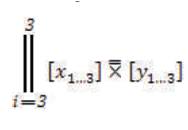
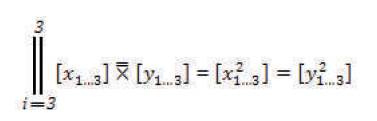

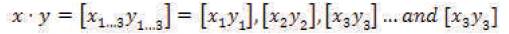
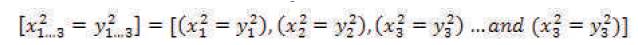
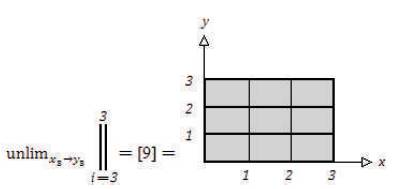

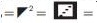 x y , and x is raised by y sequentially up to and no higher than 3, thus x2 = x3 = 9 and in parallel a single “Microcotrine”
x y , and x is raised by y sequentially up to and no higher than 3, thus x2 = x3 = 9 and in parallel a single “Microcotrine”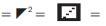 y x , and y is raised by x sequentially up to and no higher than 3, thus y3 = 32= 9 (Osler, 2013b). This is indicated by the shaded area on the aforementioned model of the Tri–Squared Proximal Positive Parallel of Square Exponent Equation graphs.
y x , and y is raised by x sequentially up to and no higher than 3, thus y3 = 32= 9 (Osler, 2013b). This is indicated by the shaded area on the aforementioned model of the Tri–Squared Proximal Positive Parallel of Square Exponent Equation graphs.