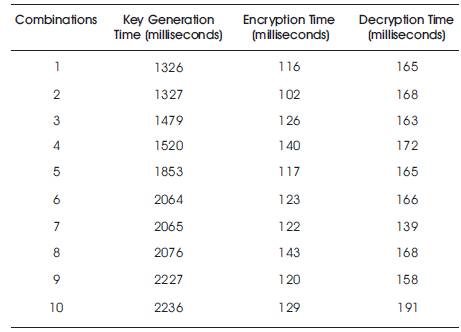
Table 1. Performance of NHSA
A New Novel Hybrid Security Algorithm (NHSA) for Rivest-Shamir-Adleman (RSA) cryptosystem was proposed in this paper, which is based on Encryption algorithm using Dual Modulus and Enhanced method for RSA (ERSA) cryptosystem. Here, the computation of public keys and private keys depends on modulus values, each computed using three different prime integers. Thus complexity involved in factorizing the modulus value increases. It improves the security of RSA scheme against Brute Force Attack using double mod operation based encryption and decryption. Therefore, it is not possible to retrieve the original message for the cipher text even after determining a single public key. Also it is difficult to factorize the modulus value into its three prime factors. Thus it enhances the security of encrypted data two times. In this paper, the proposed algorithm is compared with “Encryption algorithm using dual modulus” in terms of key generation time and security of data.
Security can be referred as a degree of protection to harm the data and resistance to harm the data. To ensure data security, confidentiality, integrity and availability of data are important (Aboud et al., 2008; Suja and Jose, 2016). Confidentiality ensures that given information can only be accessed by an authorized person. Integrity specifies the originality of data, and ensures that data is not being modified. Availability is defined as the assurance that user has access to information anytime and anywhere in the network (Ramaporkalai, 2017).
Goel (2017) has mentioned that the communication over the internet is increasing day by day, and security of data on wireless network has become vital. Nowadays it is common to exchange personal data on internet. So, data security is crucial. In order to communicate over internet, the sender has to encrypt the message or plain text with receiver ’s public key, and then receiver has to decrypt the encrypted text or cipher text using decryption key.
Ramaporkalai (2017) has concluded that Cryptography for data security is a very powerful method for protecting data, from being stolen. Cryptography is a method to encode the information, to keep the information being hacked by the third party. Jeeva et al. (2012) concluded that the most popular method of encryption is symmetric key encryption. In this method, the same key is used for both encryption and decryption process. Symmetric key encryption takes place either in block cipher or in stream cipher. As the same key is being used for both the process of encryption and decryption, the computational power of this encryption technique is small. While in asymmetric key encryption technique, different keys are used for encryption and decryption process. It is also known as public key encryption. This encryption technique is slow and impractical in case of large amount of data.
Pancholi and Patel (2016) mentioned that the hash function involves a mathematical function to irreversibly “encrypt” the data. It consist of algorithms like Message digest and hash function algorithm. Madaan and Agrawal (2012) and Osseily et al. (2008) concluded that Cloud computing is widely accepted around the world. But security of data on cloud server is a challenging issue. The best way to secure the information on cloud server is by using a security algorithm.
Verma and Garg (2014), Dongjiang et al. (2012) and Bhandari et al. (2016) have described that in conventional RSA scheme, two large prime integers say “p” and “q” are used for the computation of variable n. The security of RSA algorithm relies on the practical difficulty of factorization of product of two large integers. Ambedkar et al. (2011) have described the RSA scheme as follows.
where,
n is a modulus.
e is the public exponent or encryption exponent or simply the exponent.
d is the secret exponent or decryption exponent.
Suppose User A wants to send a message “m” to User B
User B will retrieve the original message from cipher text sent by the user A.
Panda and Chattopadhyay (2017) have used the dual modulus operation. In this algorithm, encryption as well as decryption processes are employed using double modulus operation using two private keys “e1” and “e2” and public keys “d1” and “d2” respectively. More than two large prime numbers say “p1”, “p2”, “q1” and “q2” are used for generation of modulus values say “n1” and “n2”. Dual modulus encryption technique seems to be impractical, as it takes large amount of computational time for the generation of public key and private key (Devaota et al., 2015). But it also enhances the security two times. Dual modulus algorithm is as follows:
where,
n1 and n2 are known as modulus.
e1 and e2 are known as the public exponent or encryption exponent, or simply the exponent.
d1 and d2 are known as the secret exponent or decryption exponent.
Suppose, user A wants to send message to user B.
Now, user B will retrieve the original message.
Al-Hamami and Aldariseh (2012) changed the method for generation of public and private key. In this algorithm, three large prime numbers say “p”, “q” and “r” instead of two prime numbers are used to generate public and private key. Here in ERSA, it is more difficult to factorize the modulus “n” which is a product of three different prime integers. Thus it enhances the security of conventional RSA and the steps involved in this algorithm are as follows.
where,
n is known as modulus.
e is known as the public exponent or encryption exponent, or simply the exponent.
d is known as the secret exponent or decryption exponent.
User A wants to send message “m” to user B.
User B will retrieve the message from the cipher text.
The basic idea of the proposed approach is based on Encryption algorithm using dual modulus and Enhanced method for RSA cryptosystem algorithm.
Using dual modulus in proposed algorithm, a double mod operation based encryption and decryption was introduced using two public keys say “e1” and “e2”, and two private keys say “d1” and “d2”, respectively. Using dual modulus operation in proposed algorithm improves the security of data as compared with RSA cryptosystem to very large extent. In proposed approach, even if an intruder gets succeeded in detecting a private key, still our data will be secured as it is encrypted with two different public keys. Thus the proposed algorithm is more secured than conventional RSA cryptosystem.
Enhanced method for RSA cryptosystem algorithm used in the proposed algorithm provides an idea of using three prime numbers for the calculation of each modulus value such as “p1”, “p2” and “p3” are used for the generation of “n1” and “q1”, “q2” and “q3” are used for the generation of “n2” as described by Panda and Chattopadhyay (2017). It is more difficult to factorize the modulus value into its three composite prime factors. It might increase the complexity in computation but it also enhances the security of data in the proposed approach. Here, in the proposed scheme, totally six prime numbers have been used to generate the public key and private key.
Features of proposed algorithm for RSA cryptosystem are as follows:
where,
n1 and n2 are modulus.
e1 and e2 are public exponent or encryption exponent.
d1 and d2 are private exponent or decryption exponent.
User A wants to send message “m” to user B.
User B will retrieve the original message as,
Cipher text generated by sender using message “m” is initially encrypted using “e1” to generate intermediate cipher text “c1”, and then “c1” is encrypted again using “e2” to generate final cipher text c2. Encryption process is done twice as c1 = me1 mod n and c2 = c1e2 mod n.
Same process is followed for decryption, “c2” is decrypted into “c1” using “d2”, and “c1” is decrypted using “d1” to retrieve the original message “m”. Decryption process is done twice as c1 = c2d2 mod n and m = c1d1 mod n.
Say, A want to encrypt the message m = 20
Encryption
c = ((m)e1 mod n1)e2 mod n2)
= ((21)18461 mod 20677)60457 mod 65231) = ?ô
Say, B wants to decrypt the cipher text c, then
Decryption
m = ((c)d2 mod n2)d1 mod n1)
=((?ô)42073 mod 65231)7781 mod 20677) = 20
The proposed algorithm is being compared with RSA using dual modulus on the basis of the following parameters such as
Performance of NHSA by taking various combinations of prime numbers for desired key length is given in Table 1. Ten different combinations of prime numbers of bit length 512 bits are used to generate the key of 2048 bits.

Table 1. Performance of NHSA
The proposed algorithm takes less time than RSA using dual modulus in key generation. Using both dual modulus operation and eight prime numbers might increase complexity, but it also enhances the security. Comparison of key generation time in proposed algorithm and RSA with dual modulus for various combinations of prime numbers is shown in Figure 1.
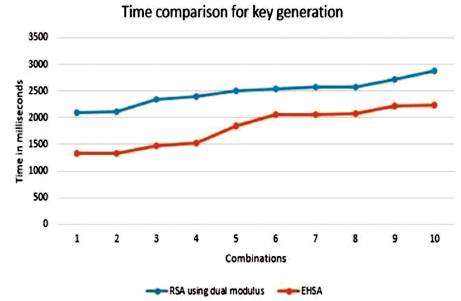
Figure 1. Analysis of Key Generation Time
The speed up (%) of NHSA and Dual Modulus RSA for Key generation is given in Table 2.
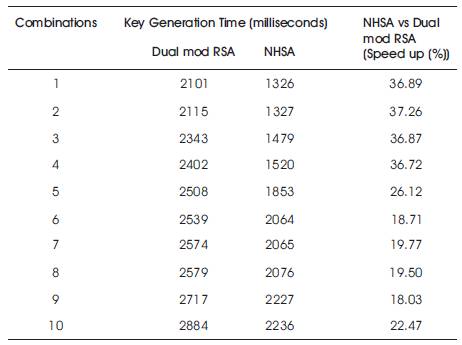
Table 2. Comparison of NHSA with Dual mod RSA in Terms of Key Generation Time
Proposed scheme is more secured as compared to conventional RSA cryptosystem, ERSA and RSA with dual modulus. Proposed scheme is using double encryption and decryption with two different public keys and two different private keys along with eight prime integers, which has been used instead of four or six prime integers, for the computation of modulus value n1 and n2. Hence it enhances the security of information or data to a very large extent.
In the proposed scheme, six prime numbers are used, and encryption and decryption has been done twice which might increase the computational complexity and the encryption and decryption time. It also enhances the security two times as compared to conventional RSA cryptosystem, and also it reduces the key generation time than RSA using dual modulus. Also, it is more secured against the Brutal Force Attack than conventional RSA. Even if an intruder detects the private key, it is not possible to retrieve the information from the cipher text as the sender has encrypted the information twice.
Therefore, this proposed algorithm improves the performance and security of RSA using dual modulus.