In this paper a principal neighborhood dictionary nonlocal means method is proposed. As the computational power increases, data-driven descriptions of structure are becoming increasingly important in image processing. Traditionally, many models are used in applications such as denoising and segmentation based on the assumption of piecewise smoothness. Unfortunately, these models yield limited performance thus motivated for data driven strategies. One data-driven strategy is to use image neighborhoods for representing local structure and these are rich enough to capture the local structures of real images, but do not impose an explicit model. This representation has been used as a basis for image denoising and segmentation. But the drawback is it gives high computational cost. The motivation of our work is to reduce the computational complexity and higher the accuracy by using nonlocal means image denoising algorithm. This paper will present in-depth analysis of nonlocal means image denoising algorithm that uses principal component analysis to achieve a higher accuracy while reducing computational load. Image neighborhood vectors are projected onto a lower dimensional subspace using PCA. The dimensionality of this subspace is chosen automatically using parallel analysis. Consequently, neighborhood similarity weights for denoising are computed using distances in this subspace rather than the full space. The resulting algorithm is referred to as principal neighborhood dictionary nonlocal means. By implementing the algorithm we will investigate principal neighborhood dictionary nonlocal means method's and nonlocal means method's accuracy with respect to the image neighborhood and window sizes. Finally, we will present a quantitative and qualitative comparison of both methods.

In image processing, data-driven descriptions of structure are becoming increasingly important. Traditionally, many models are used in applications such as denoising and segmentation have been based on the assumption of piecewise smoothness [1], Unfortunately, this type of model is too simple to capture the textures present in a large percentage of real images. This drawback has limited the performance of such models, and motivated data driven representations. One data-driven strategy is to use image neighborhoods or patches as a feature vector for representing local structure. Image neighborhoods are rich enough to capture the local structures of real images, but do not impose an explicit model. This representation has been used as a basis for image denoising [2]-[4], for texture synthesis [5], and for texture segmentation [6]. For both denoising and segmentation, it has been demonstrated that the accuracy of this strategy is comparable to state-of-the-art methods in general and exceeds them in particular types of images such as those that have significant texture patterns. The drawback is the relatively high computational cost. The image neighborhood feature vector is typically high dimensional. For instance, it is 49 dimensional if 7 X 7 neighborhoods are used. Hence, the computation of similarities between feature vectors incurs a large computational cost. One motivation of our work is to reduce the computational complexity of methods that rely on image neighborhood information. The Nonlocal Means (NLM) image denoising algorithm averages pixel intensities using a weighting scheme based on the similarity of image neighborhoods [1]. The use of a lower dimensional subspace of the space of image neighborhood vectors in conjunction with NLM was first proposed in [2]. A very similar approach that uses covariance matrices instead of correlation matrices for subspace computation is given in [3]. In these methods, which we refer to as Principal Neighborhood Dictionary (PND) NLM, the image neighborhood vectors are projected to a lower dimensional subspace using Principal Component Analysis (PCA). Then, the neighborhood similarity weights for denoising are computed from distances in this subspace resulting in significant computational savings. More importantly, it is also shown that this approach results in increased accuracy over using the full-dimensional ambient space [2],[3]. While it is clear that a global sample of image neighborhoods cannot be represented in a reduced dimensionality linear subspace, the increased accuracy can be attributed to the robustness of the similarity criterion to noise. In other words, pair wise distances computed in the subspace defined by the significant eigenvectors of principal component decomposition are more robust to additive noise than distances computed in the full-dimensional space. Another closely related paper uses singular value decomposition of the image neighborhood vectors for selecting the patches to be used in averaging [4]. One disadvantage of the approach in [10] is the introduction of a new free parameter to the algorithm—the dimensionality of the PCA subspace. In [8] Eigenvalues of the data correlation matrix to the noise variance to determine the subspace dimensionality are compared. In this paper, we propose an automatic dimensionality selection criteria using parallel analysis that eliminates this free parameter[9]. Compared to [2], our criteria does not require the estimation of noise variance and is shown to produce a more conservative estimate of dimensionality. We present a detailed analysis of the performance of the method with respect to subspace dimensionality and demonstrate that the dimensionality selection by parallel analysis provides good results. More recently, parallel analysis has been proposed as a way to determine the number of models in shape analysis [7]. In [1] the NLM image denoising algorithm which averages pixel intensities weighted by the similarity of image neighborhoods is introduced. Image neighborhoods are typically defined as 5x5, 7x7, or 9x9 square patches of pixels which can be seen as 25, 49 or 81 dimensional feature vectors, respectively. Then, the similarity of any two image neighborhoods is computed using an isotropic Gaussian kernel in this high-dimensional space. Finally, intensities of pixels in a search-window centered around each pixel in the image are averaged using these neighborhood similarities as the weighting function. More recently, in [6] an adaptive search-window approach which attempts to minimize the L2-risk with respect to the size of the search-window by analyzing the bias and variance of the estimator have been introduced. In [8] a method to improve the computational efficiency of the NLM algorithm. is proposed. The patch selection method removes unrelated neighborhoods from the search-window using responses to a small set of predetermined filters such as local averages of gray value and gradients. Unlike [8] the lower dimensional vectors computed in [2]–[4] are data-driven. Additionally, in [2] and [3], the lower dimensional vectors are used for distance computation rather than patch selection.

Starting from a discrete image u, a noisy observation of u at pixel i is defined as v(i)=u(i) +n(I) Let N_i, denote a _{r x r}, square neighborhood centered around pixel i. Also, let y(I), denote the vector whose elements are the gray level values of at pixels inN_i, Finally, S_i is a square search-window centered around pixel i . Then, the NLM algorithm defines an estimator for u_i, as

 

Where 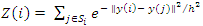 is a normalizing term, the smoothing kernel width parameter h controls the extent of averaging. For true nonlocal means, the search window S_i, needs to be the entire image for all I, which would give rise to global weighted averaging. However, for computational feasibility S_i, has traditionally been limited to a square window of modest size centered around pixel i . This is the limited-range implementation of the NLM algorithm as proposed in the pioneering work by [1]. For instance, a 21 x 21 , window is used in [5] whereas a 7 x 7 , window is used in [2]. We investigate the search window size's effect.

The success of the NLM algorithm is attributed to the redundancy that is available in natural images. Constant intensity regions present no problem as there are a very large number of copies of similar neighborhoods in such areas of the image. Edges and other 1-D structures also have a relatively large number of copies of similar neighborhoods located along the structure of interest. The hardest case is that of intensity configurations that occur in textured regions. Buades et al. show that even in such cases, one can find similar neighborhoods if the search-window S is sufficiently large [1].

The distances ll y(i) - y(j) ll² in are replaced by distances computed from projections of y onto a lower dimensional subspace determined by PCA. In the rest of this paper we will refer to this method as the PND NLM algorithm. Let Ω denote the entire set of pixels in the image. Also, let Ψ be a randomly chosen subset of Ω. Treating y(i) as observations drawn from a multivariate random process, we can estimate their covariance matrix as

 

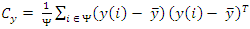
Where 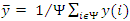 is the sample mean and Ψ is the number of elements in the set Ψ. A small subset ΨΩ is typically sufficient to accurately estimate the covariance matrix and results in computational savings. The dimensionality of a _{r x r} , neighborhood vector is r² . For simplicity of notation, let M=r² . Then c_y is a M x M matrix. Let {b_p: = 1: d} be the eigenvectors of c_y , i.e., the principal neighborhoods, sorted in order of descending Eigen values. Let the d-dimensional PCA subspace be the space spanned by {b_p: = 1: d}.

Then the projections of the image neighborhood vectors onto this subspace is given by 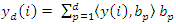 Where {y(i), (b₁)} denotes the inner product of the two vectors.

Let 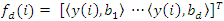 be the d-dimensional vector of projection coefficients. Then, due to the ortho- normality of the basis functions

 

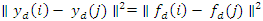
Finally, are define a new family of estimators for d€[1,m]

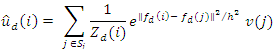
Significant principal neighborhoods are extremely robust to additive, independent and identically distributed noise. It is known that principal directions of a multivariate probability distribution function are not altered by addition of spherically symmetric noise. Therefore, for infinite sample sizes, the eigenvectors of the covariance matrix of image neighborhoods will not be altered by addition of independent and identically distributed noise to the image. Eigenvalues will be increased by the noise variance amount. The effects of noise on the Eigenvalues of finite sample covariance matrices have also been previously investigated. Experimental evidence suggests that principal neighborhoods that correspond to the larger Eigenvalues of the covariance matrix do not change in any noticeable way in the presence of noise.

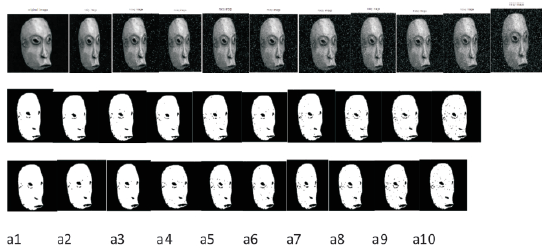
Figure 1. Skull

Figure 2. Dice

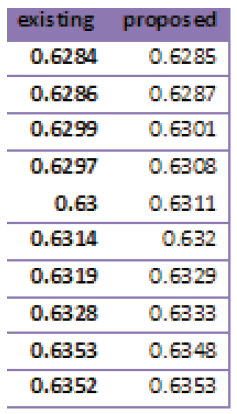
Table 1. Skull

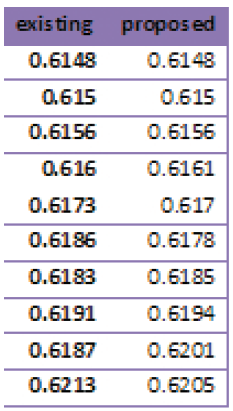
Table 2. Dice

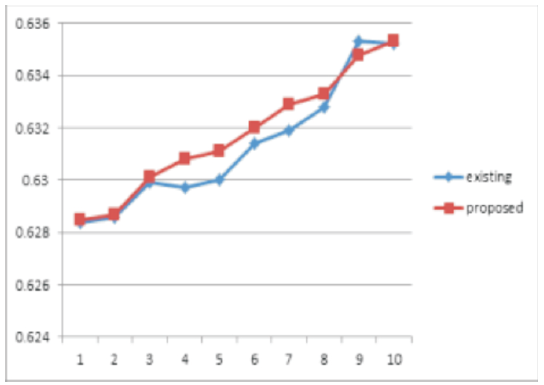
Figure 1. Skull

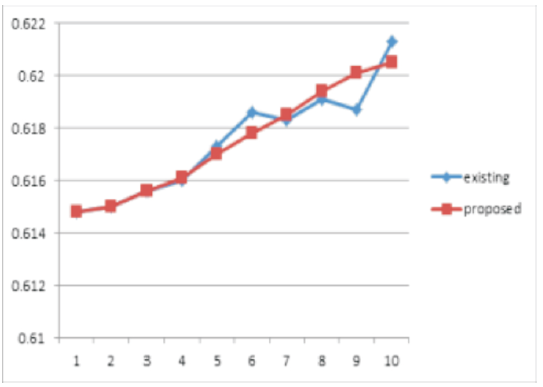
Figure 2. Dice

In this paper, we evaluate the proposed method by several experiments on different database images, and compared the output images of Gaussian, salt and pepper noises with ground truth images by jacquard method and placed in the tables, drawn the graphs and shown the ground truth, noisy and output images. Jacquard similarity coefficient method is very popular and used mostly as similarity indices for binary data. The area of overlap A_j is calculated between the thresholded binary image B_j and its corresponding gold standard image G_j as shown below

 

If the thresholded object and corresponding gold standard image G_j (associated ground truth image) are exactly identical then the measure is 0 and the measure 1 represents they are totally disjoint, but the higher measure indicates more similarity. This demonstrates the superiority of the proposed method. The proposed method confirms the qualitative improvement over the traditional methods.

In this paper, the lower dimensional projections are not only used as a search criteria but also for computing similarity weights resulting in better accuracy in addition to reduced computational cost. In the experimental results first row images are noisy images, second row images are output of existing method (NLM) and third row images are output images of proposed method (PND). It is clear that image neighborhoods can't be modeled in a global, linear subspace. The NLM algorithm has been applied to images by measuring distance in the image neighborhood space. The Principal Neighborhoods approach can also be easily applied to other denoising and segmentation algorithms that use similarity measures based on image neighborhood vectors.