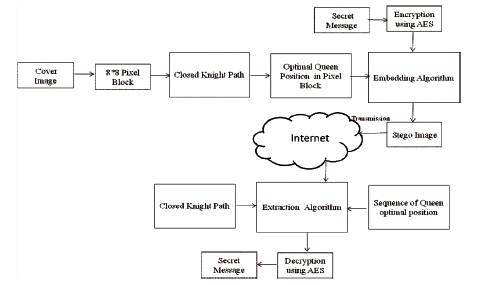
Figure 1. Data Hiding Approach using Optimal Selection of Queen Position Along Knight Tour
A knight tour starts from any square of the chessboard. A tour in which a knight visits every square on the board exactly once is called closed knight tour. A queen can move along column, row and diagonal in both forward and backward direction. In proposed method, the authors divide the cover image into non-overlapping 8x8 pixel blocks. For each block, they place a queen on a square and find the number of prime attacking positions by the queen along knight tour. Then the authors remove these attacking positions from the sequence of knight tour in 8x8 bytes block. They compute number of mismatches between bits in LSB position in 8×8 bytes blocks and corresponding number of bits from encrypted message to be hidden. The queen position that results in minimum distortion is chosen. The process is applied on each block in the cover image. The queen positions determined during embedding phase is recorded as the key and the same is used to extract the hidden message from stego cover. Experimental results performed on different images reveal that this method maintains high degree of imperceptibility. Randomization achieved through knight tour and queen moves provide another level of security against detection.
Due to advancement in computer technology, Internet plays an important role in communication or exchange of information using public data network. It becomes important to protect information, once it is on the public data network, from various security risks and consequent threats. One of the methods to protect information is to hide it with another innocuous looking cover media. Conceptually, hiding information can be thought of similar to protecting a soldier in battlefield. Generally, there are some methods used to protect soldiers form enemy(U.S. Army Infantry School, 1984). It is cover, concealment and camouflage. “Cover” as bunker is used to protect from bullets and bombs. “Concealment” protects the soldier from enemy's observation. On the other side “Camouflage” means concealing of personnel or equipment from an enemy by making them appear to be a part of the natural surroundings. Similarly, Steganography deals with information hiding. Basically, it is a technique to embed secret message into a digital cover with least or no distortion. It is blended into the digital cover. Another way of protecting information is cryptography. It is a technique of transforming (encrypt) a plain text into an unreadable format, called cipher text (W.Stallings, 1999). Only those who possess a secret key can decipher (decrypt) the message into plain text.
In the reverse side, steganalysis plays important role to expose the presence of hidden secret information in a media and cryptanalysis is used to decipher the message into original form. The digital media that is used to hide message is called cover and the digital media containing data is called the stego. As bytes in the cover are modified, the cover is distorted. Overall goal of any steganography is to optimize robustness, imperceptibility and capacity. A fine balance is achieved when distortion produced by steganographic method is kept to the minimum possible.
Steganographic method can be classified into two main categories: spatial domain (Mielikainen, 2006; Chan & Cheng, 2004; Muttoo, Kumar & Bansal, 2012, Thanikaiselvan & Arulmozhivarman, 2012, Kumar, Bansal & Muttoo, 2014) and frequency domain (Muttoo & Sushil, 2009a, 2008, 2013). In spatial domain, the most popular steganography approach are based on LSB (Mielikainen 2006; Kumar, Bansal & Muttoo, 2015) in which the least significant bits of bytes in a digital cover are modified with the message bit stream. There are some effective steganographic methods (Mielikainen, 2006; Bajaj, Bedi & Pal, 2010; Iranpour, Mehran & Safabakhsh, 2014) that mainly focus on optimal pixel modification to achieve the minimal distortion. Mielikainen (2006) proposed LSB matching revisited method. In this method, two data bits are embedded to a pixel pair by modifying at the most one pixel of which the pixel value is either added or subtracted by one. Bajaj et al (2010) proposed a new data hiding scheme for message of variable length based on Particle Swarm Optimization. This method gives the optimal position in the cover image, which is used to hide message. Zhang and Wang (2006) proposed the exploiting modification direction (EMD) embedding, in which secret digit in a (2n+1)-ary notational system is carried by n cover pixels and at most, only one pixel is increased or decreased by one. The relative payload is log(2n+1)/n bpp in this method. Amirtharajan and Rayappan (2012) proposed an Adaptive Random (AR) kbit embedding approach which attempts to enhance the quality of the stego image. Similarly, Iranpour et al proposed an image steganographic method which employs the Hamiltonian paths in order to decrease the distortion produced by the LSB substitution scheme (Iranpour & Safabakhsh, 2014). Hamiltonian paths are checked for data embedding twice; one time for the original binar y data and another time for the complement of data. The best paths, which provide the minimal distortion for the blocks, are recorded and kept as the secret key. In this method, secret key is not embedded into cover image. It is shared between sender and recipient separately.
In this paper, the authors have presented a multiple randomization data hiding method based on closed knight tour and optimal selection of queen in 8×8 blocks. In this method they select optimal position of queen in 8×8 block so that less image distortion and high embedding capacity can be achieved. Closed knight tour (Borrell, 2009; Bansal, Muttoo & Kumar, 2015) and optimal queen position in 8×8 block together provide multiple randomizations in selection of pixels (bytes) for message hiding. The proposed framework for embedding message in a cover image is shown in Figure 1.

Figure 1. Data Hiding Approach using Optimal Selection of Queen Position Along Knight Tour
The paper is organized in six sections. Section 1 presents the basics of Knight-Queen Chessboard puzzle in 8×8 block. Embedding and Extracting algorithm is discussed in Section 2. Experimental results are presented in the Section 3. Security analysis of the embedding algorithm is discussed in Section 4 and the paper is finally concluded in Section 5.
Knight tour is a chess puzzle (Borrell, 2009; Lobbing & Wegener 1996; McKay & Brendan, 1997, Douglas, 2014). The objective of this puzzle is to find a path on a chessboard such that a knight moves to each square on the board exactly once as shown in Figure 2. Knight tour has two variations: closed knight tour and open knight tour. Closed Knight Path ends on the same square it started from while open knight path does not have this restriction. For many years, Mathematicians and Computer Scientists have devoted their time and effort to solving this problem and it was observed that there was no one unique solution to find. Lobbing et al first calculated a number of knight tour equals to 33,439,123,484,294 on the standard 8×8 chessboard (Lobbing & Wegener, 1996). Further, McKay created a computer program to calculate the total number of undirected knight's tours and result was proposed 13,267,364,410,532 on the standard 8×8 chessboard (McKay & Brendan 1997). McKay also claimed that the Lobbing implementation of algorithm was performed incorrectly, leading to a wrong answer.
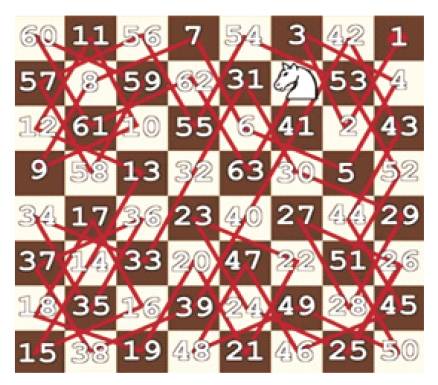
Figure 2. Closed Knight Tour in 8×8 Block
G. L. Honaker presented an interesting problem on chessboard (Honaker, 2004). It is based on knight and queen pieces on chessboard. In this problem, First any knight's tour is created on an 8x 8 chessboard, in which the knight starts on any square of the board and by successive knight moves visits every square on the board exactly once. Number the squares visited by the knight is in order starting with 1 from the starting square as shown in Figure 2. Then, we place a Queen on any square and count the number of prime numbers attacked by the Queen (Here the Queen is not considered to be attacking the square it sits on) as shown in Figure 3.

Figure 3. Placement of Queen in Closed Knight Tour
Figure 3 illustrates a closed knight path on 8×8 chessboards. Let a queen be placed at the position of 63. We find the prime position of attack by queen along closed knight path. The result is 11, 59, 53, 41, 13, 5, 23, 47 and 51. In our method, the pixels which are on prime location and attacking by queen will not participate in hiding. Therefore, the hiding path is 1 ,2 ,3 ,4 ,6 ,7 ,8 ,9 ,10 ,12 ,14 ,15 ,16 ,17 ,18 ,19 ,20 ,21 ,22 ,24 ,25 ,26 ,27 ,28 ,29 ,30 ,31 ,32 ,33,34 ,35 ,36 ,37 ,38 ,39 ,40 ,42 ,43 ,44 ,45 ,46 ,48 ,49 ,50 ,52 ,54 ,55 ,56, 57 ,58 ,60 ,61 ,62 ,63 and 64. The selected path is multiple randomized paths based on closed knight tour and optimal queen position as shown in Figure 4.
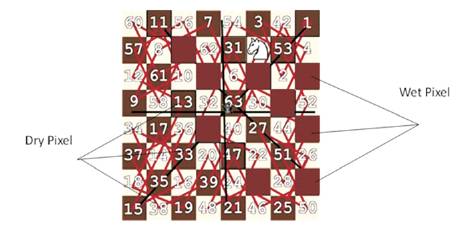
Figure 4. Randomized path using Closed Knight Tour and placement of Queen
Fridrich et al. proposed a steganography method called writing on wet paper. The method is based on the concept of wet and dry spots in a cover. Imagine that a cover is exposed to rain in such a way that some of its spots become wet and the rest remain dry. A sender can only modify the dry spots of the cover image to hide a message. In the proposed method, we partition an image cover in 8x8 bytes blocks. We place a queen on a square and find the number of prime attacking position by the queen along knight tour. Then we remove these attacking positions from the sequence of knight tour in 8x8 bytes block. A path that provides the maximum similarity between the LSB of the bytes and the secret data bits is selected. Each such path has two types of pixels: a wet pixel (byte) is the byte position along closed knight path that are in prime attacking position of queen and the rest are dry pixels (bytes) as shown in Figure 4. The sender can only modify the dry pixels of the cover image.
The LSB bits of wet pixels are not considered in matching with secret data. This process is repeated and the queen position that results in minimum distortion along closed knight tour is chosen. Finally, optimal positions of queen as well as mismatched pixels are recorded. This process is repeated for all blocks. Dry pixels that are modified during embedding and the position of queen along closed knight path is determined. The optimal positions of queen in all blocks are recorded and it is used as stego key. It is communicated using Diffie - Hellmen key exchange method (Stallings, 1999). The pseudo-code of embedding method is given below.
Embedding Algorithm
Inputs – C: the cover image M: the encrypted message
Outputs – S: the stego-image Q: sequence of optimal queen position in 8×8 blocks K: the knight path
Step 1: Take cover image C and divide it into 8×8 pixel blocks Bi
Step 2: The pixel positions in Bi are represented by P(j,k) where 1 ≤ j ≤ 8 and 1 ≤ k ≤ 8
Step 3: Select one knight path K from 13,267,364,410,352 existing solution in 8×8 block.
Step 4: Let Bi be the first block and Mi be the first bit of message
Step 5: Select the path for embedding Mi into the LSB of the pixels of Bi where distortion is minimum
Step 5.1: Let Min = 64
Step 5.2: For j = 1 to 8
Step 5.3: For k = 1 to 8
Step 5.4: Let Pi,k in Bi is optimal position of Queen.
Step 5.5: Find the prime positions in Bi along knight path which is attacked by queen and consider it as wet pixels.
The rest of pixels in Bi are considered as dry pixels.
Step 5.6: Calculate the number of mismatches in block Bi by embedding Mi into LSB of dry pixels in Bi along the knight path and result is stored in MISS.
Step 5.7: Compare Min > MISS
Step 5.8: Min = MISS
Step 5.9: Qpos = Pj,k
Step 5.10: Next j
Step 5.12: Next k
Step 6: Queen's position Qpos in Bi along knight path is stored in Q as a key.
Step 7: Modify the LSB of the dry pixels in Bi with binary sequence of Mi along the best optimal path.
Step 8: Go to the step 5 and look for hiding in the next 8×8 pixel block Bi+1
For data extraction, knight path and sequence of optimal position of queen should be shared between sender and recipient. Using this information, the optimal path is determined. Similar to the embedding procedure, the stego image is divided into 8×8 blocks. Further, the dry pixel (byte) is identified by placement of queen in 8×8 blocks and then extracts the LSB of the dry pixels (bytes) along knight path.
Inputs: K: the knight path S: the stego image Q: sequence of optimal queen position in 8×8 blocks
Output – M: the encrypted binary data
Step 1: K is the knight path in a 8×8 block
Step 2: Divide cover into 8×8 blocks.
Step 3: Take the optimal queen position from Qi for first 8×8 block
Step 4: Find the sequence of dry pixel along knight path for extracting the message bit.
Step 5: Extract bits from the LSB of the dry pixels along knight path and store in Mi
Step 6: Take the next block and repeat step 3 to 5 until data is completely extracted
In this section, some experimental results are presented to show the efficiency of the presented method. The authors have tested the algorithm using about 1000 images of size 256×256 pixels. These images are taken from different sources including self snapped images using own digital camera. The codes are implemented using C and MATLAB 7.10(R2009b).
To assess the visual quality of a stego, the authors have used the Peak-Signal-to-Noise Ratio (PSNR) as the measure of distortion due to data hiding. The PSNR is defined as follows:
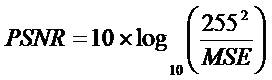
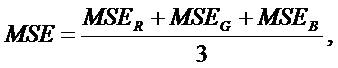
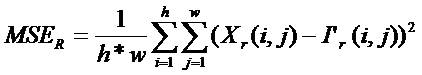
where Xr(i, j) and I'r (i, j) represent the pixel values located at (i, j) in the original image and the stego image, respectively. The symbols h and w represent the height and width, respectively of the images. The PSNR value of greater than 30dB is considered as safe value for retaining the similarity between cover and stego images (Petitcolas et al., 1999). In such cases, it becomes difficult for human eyes to distinguish stego image from its corresponding cover image.
Several experiments to determine the influence of quality of the stego image in the presented method. Results obtained on some standard images are tabulated in the Table 1.
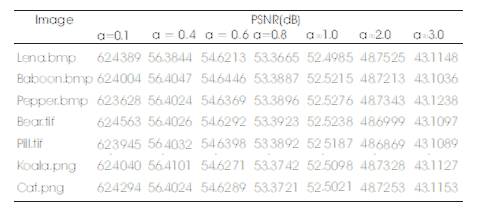
Table 1. The Average of the PSNR (dB) Value for some Relative payloads (bits per pixel) in the presented method for different images
A comparative study between the proposed algorithm and some other steganographic methods is carried out to assess the payload capacity. The result so observed is tabulated in the Table 2.
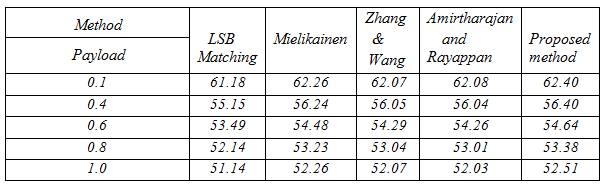
Table 2: Comparison of the average PSNR (dB) value for some relative payload α (bpp) in the presented method and some other methods
The embedding method modifies the pixel values based on match/mismatch between LSB of the selected pixel and the secret message bit. Percentages of mismatch bits on different payload are shown in Figure 5. This helps in analyzing the effect of embedding payloads in the cover by studying intensity histogram of the stego.
The result of experiments is shown in Figure 5. It shows the probability of mismatch bits (1 bit per pixel) on different image of various payloads.
The overall reduction in the expected number of modification per pixel is estimated by following equation Expected number of modification per pixel =
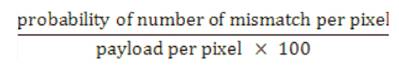
In the Figure 5, It is shown that if number of modified bits is 0.1 bit per pixel (10% of LSB bits in the cover) then number of mismatch bit in 1bpp is 3.8%. Therefore, the expected number of modification per pixel is 3.75/ 0.1*100 =0.375. Similarly, if embedding payload is 0.4 bit per pixel (40% of LSB bits in the cover) then the number of mismatch bit in 1 bpp is approx 15. Therefore, the expected number of modification per pixel is 15/ 0.4*100 = 0.375. If embedding payload is 0.6 bit per pixel (60% of LSB bits in the cover) then the number of mismatch bit in 1 bpp is approx 22. Therefore, the expected number of modification per pixel is 22/ 0.6*100 = 0.366. If embedding payload is 0.8 bit per pixel (80% of LSB bits in the cover) then the number of mismatch bit in 1 bpp is approx 30. Therefore, the expected number of modification per pixel is 30/ 0.8*100 = 0.375. If embedding payload is near to 1 bit per pixel then the number of mismatch bit in 1 bpp is approx 32.5. Therefore, the expected number of modification per pixel is 32.5/ 1*100 = 0.325.
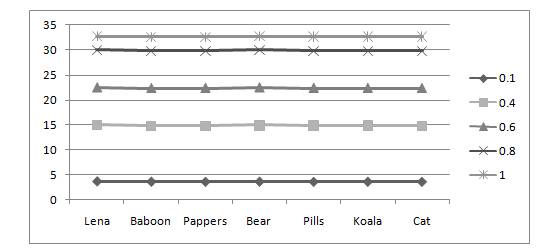
Figure 5: Graph for Mismatch bits (1 bpp in %) and payload per pixel on different image
From all the above results, It is shown that the probability of mismatch bits would be near 0.325 to 0.375 per bit pixel to embed the secret message as a random sequence of 0 and 1. This is better than the LSB replacement and LSB matching, which is 0.5 pixels per message bit. Hence, the proposed method improves the embedding efficiency from 1.25 to 2 bits per embedding change. This low probability effectively reduces the probability of detection with LSB based steganalysis methods like the Sample Pair (SP) analysis (Dumitrescu, Wu & Wang, 2003) and Weighted Stego (WS) (Ker & Bohme, 2008) .
The proposed method provides multilayer protection due to randomness in selection of closed knight tour based on optimal placement of queen. The optimal position of queen is recorded as key and it is used in the extraction process of hidden message. Encryption of message, before hiding, provides another layer of security.
The authors have presented a digital steganographic technique in which LSB selection in digital cover is randomized using optimal placement of queen along closed knight tour. Optimality is determined when maximum similarity between the LSB of bytes in a 8×8 block along selected knight tour path and the corresponding secret data bits is achieved. We check different knight tour paths by considering the prime attacking positions when a queen is placed in a square in 8×8 block. The knight path provides the first layer of security. The proposed method also generates a sequence of queen position along knight path for each block. This sequence is shared between communication partners: the sender and the recipient. This sequence acts as steganographic key. The sequence of queen position provides an additional layer of security of our steganographic method. A steganographic technique is evaluated for its robustness, imperceptibility and capacity. The proposed method achieves the goal as supported by the experimental results presented in the Section 4 of the paper. As a future work, this randomization technique may be tested with other steganographic schemes that work in other domains for improving embedding capacity and security.
We are very thankful to all those who have been constantly encouraging and providing required resources for such scientific research work besides the regular works which we are doing in our respective departments. We are also thankful to our colleagues and seniors for their continuous support and encouragement. We are grateful to all those who provided suggestions for improvement of this work.