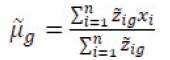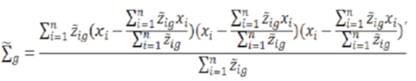Abstract

Clustering is collection of data objects that are similar to one another and thus can be treated collectively as one group. The model based clustering approach uses model for clustering and optimizes the fit between the data and model. The evolutionary algorithm has the ability to thoroughly search the parameter space, providing an approach inherently more robust with respect to local maxima. In EvolvExpectation-Maximization(EvolvEM)algorithm,Expectation Maximization and Genetic algorithm is used for clustering data which shows more efficiency then EM clustering. The drawback in this method is that its execution time is higher and it requires more parameters. In the proposed approach, instead of Genetic algorithm, Bee colony optimization can be combined with Expectation Maximization algorithm in order to improve execution time and clustering efficiency. Hence, it can be efficiently used for clustering.

Data Mining, also popularly known as Knowledge Discovery in Databases (KDD), refers to the nontrivial extraction of implicit, previously unknown and potentially useful information from data in databases. Data mining mechanisms has been applied in business and manufacturing companies across many industrial sectors. Data mining encompasses a number of different technical approaches such as clustering. The overall goal of the data mining process is to extract information from a dataset and transform it into an understandable structure for further use. Data mining can be performed in a variety of information repositories.

Clustering is a process of partitioning a set of data (or objects) into a set of meaningful sub-classes, called clusters. It is the main task of explorative data mining. Clustering is the task of assigning a set of objects into groups called clusters, so that the objects in the same cluster are more similar to each other but the objects in different clusters are dissimilar. Clustering techniques try to group objects based on similarity (distance) measure. Clustering is especially useful in the condition when there is little knowledge about the given dataset.

1.1 Model-Based Clustering

It attempts to optimize the fit between the data and mathematical model. Statistical and AI approach in model based clustering are Conceptual clustering and COBWEB.

Expectation-Maximization algorithm is a general approach to MLE or MAP problems in which the data can be viewed as consisting of N multivariate observations (X ,Z ) where X is observed and Z is unobserved. If (X ,Z ) are independent and identically distributed according to a probability distribution P with parameter q then the complete-data likelihood Lc is

[1]

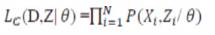
The observed data likelihood Lo can be obtained by integrating out Z from the complete-data likelihood,

[2]

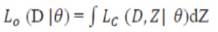
The MLE for q based on the observed data maximizes L o (D/q) with respect to q Without knowing the data, the EM algorithm alternates between two steps. In the E-step, the conditional expectation of the complete-data loglikelihood given the observed data and the current parameter estimates is computed. In the M-step, the parameters that maximize the expected log-likelihood from E-step are determined.

[3]

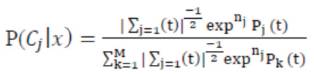
To compute the covariance matrix for the next iteration the Bayes Theorem is applied, which implies that P(A|B) based on the conditional probabilities of the class occurrence. The probability of occurrence of each class is computed through the mean of probabilities (C ) in j function of the relevance degree of each point from the class.

[5]

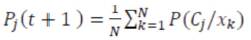
Finite mixture models use a convex combination of probability densities to model data that arise from two or more subpopulations. Using finite mixture models to cluster data is a natural approach and is known as modelbased clustering.

Matrinez and Vitia (2000)[1]proposed two algorithms for clustering. The first algorithm(Expectation-Maximization + Genetic Algorithm) is useful when information of the observed data is not available. This algorithm uses a population of mixture models that evolves in time in an attempt to overcome the local maxima problem. The second algorithm ( EM+ GA+ Knowledge) is useful for those cases where some knowledge of the structure of the data set is known. This gives additional knowledge of the underlying structure to be learned. Both algorithms have proven to be superior to the typical EM implementation for the spiral shape data, under same computational condition.

Deb(2001)[5]proposed a new approach that mainly focuses on two main areas: i) multi-objective evolutionary algorithms (MOEAs) with different variation operators and ii) decrease of the cardinality of the resulting population of MOEAs. The outcome of the former is a comparative analysis of MOEA versions using different variation operators on a suite of test problems. The future area has given rise to both a new branch of Multi Objective Optimization (MOO) called MODCO (Multi-Objective Distinct Candidates Optimization) and a new MOEA which makes it possible for the user to directly set the cardinality of the resulting set of solutions.

Pernkopf and Bouchaffra (2005)[4]proposed a Geneticbased Expectation-Maximization (GA-EM) algorithm for learning Gaussian mixture models from multivariate data. Algorithm is capable of selecting the number of components of the model using the Minimum Description Length (MDL) criterion. The population-based stochastic search of the GA explores the search space more thoroughly than the EM method. The approach is less sensitive to the initialization compared to the standard EM algorithm. Since the GA-EM is elitist it maintains the monotonic convergence property of the EM algorithm. One drawback of the GA-EM algorithm is that it requires additional parameters.

Bouveyron et al (2007) [2] proposed clustering approaches which estimate the specific subspace and the intrinsic dimension of each class. The approach adapts the Gaussian mixture model framework to highdimensional data and estimates the parameters which best fit the data. It is a robust clustering method called High- Dimensional Data Clustering (HDDC). Apply HDDC to locate objects in natural images in a probabilistic framework. High-dimensional data usually live in different low dimensional subspaces hidden in the original space.

Karlis and Santourian (2009)proposed a mixture of the Multivariate Normal Inverse Gaussian (MNIG) distribution. The MNIG distribution is obtained as a mean-variance mixture of multivariate normal distributions with an inverse Gaussian mixing distribution. As the inverse Gaussian density allows for closed form ML estimates, it is easier to handle in the finite mixture setting than the gamma density. This is also true when skewed versions of the multivariate t -distribution are involved and makes the finite mixture of MNIG distribution much more useful in practice than the corresponding mixtures of multivariate skew-t distributions.

The existing GA based clustering algorithm does not produce optimal clustering results and requires many parameters to adjust.

The proposed method aims at performing model based clustering with less number of parameters using EM and GA algorithms.

Andrews (2013) [6]proposed an approach that casts the model- fitting problem as a single objective evolutionary algorithm focusing on searching the cluster membership space. The EAs are used to solve optimization problems using survival of fittest principle.

5.1 EM Clustering

The EM algorithm is often utilized for mixture model parameter estimation. The EM algorithm is an iterative procedure for parameter estimation in the presence of missing data that alternates between Expectation (E-) and Maximization (M-) steps. In the E-step, the expected value of the complete-data log-likelihood is computed. The Mstep maximizes the expected value of the completedata log-likelihood with respect to the unknown model parameters.

For model based clustering, initialization requires either specifying starting values for the cluster membership indicators and using maximum likelihood estimation to solve for the model parameters or specifying initial model parameters and calculating the expected values of the cluster membership indicators. Following initialization, the algorithm cycles between E- and M-steps until some convergence criterion is met. Here, the expected value of the component membership indicators is

[6]

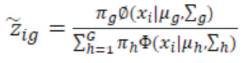
During the E-step, replace zig by in

to get the expected value of the complete-data loglikelihood. During the M-step, the expected value is maximized resulting in the updates:

[7]

[8]

[9]

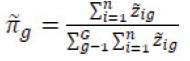
EM algorithms and variants used in mixture modelling applications are usually single-path-monotonic and deterministic. This means that, given any initialization, the algorithm will follow the same single, monotoneincreasing path to convergence. Monotonicity increases because parameter estimates can only improve (according to the log-likelihood) as the algorithm progresses. However, combining monotonicity with a singular search path is complicated.

5.2 EM with genetic algorithms

Evolutionary Algorithm is broadly defined and is applicable to many optimization problems. EAs are single-objective or monotonicity built to optimize one or more fitness functions.

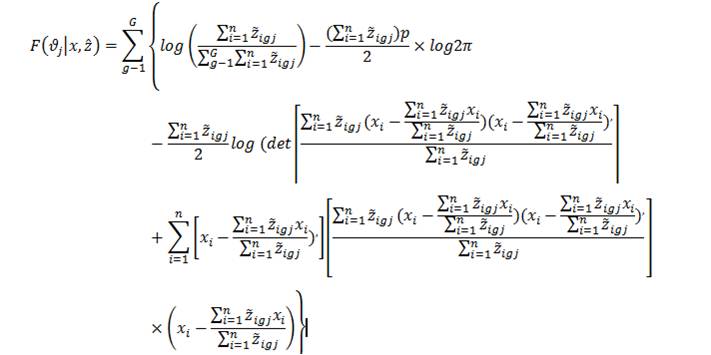
5.3 Survival

K solutions with the best associated log-likelihoods from each generation will survive. In addition, K solutions will be cloned to the next generation, ensuring that the top K solutions for each generation are monotonically increasing.

5.4 Reproduction

Random mutations will be generated within 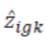the at each reproduction stage according to a approach. Each of these offspring will have a 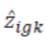mutated for one value of i such that its cluster membership changes. The mutating multiple observations to produce an offspring was considered, but the resulting algorithms consistently under-performed when compared to the single-mutation algorithm in terms of both efficiency and accuracy. Given the maximum likelihood estimates resulting from the initial 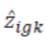the expected values 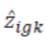is given by

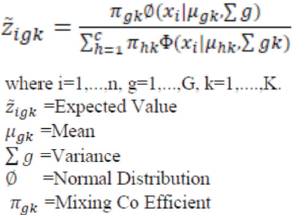
Mutate the 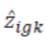by randomly sampling each observation's cluster membership according to the probability. Store K parents to each iteration and in reproduction phase, sample j/k new 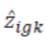matrices according to the each k parents 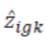surface and a singularity-riddled surface, and that results in high susceptibility to attaining local maxima instead of global maxima.

Because each step of the algorithm will require calculation among either parents or offspring, this is both intuitively appealing and facilitates easy comparison with the EM algorithm. The difference between the EM algorithm and fitness function is that it uses 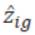instead of .

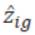6. Result Analysis

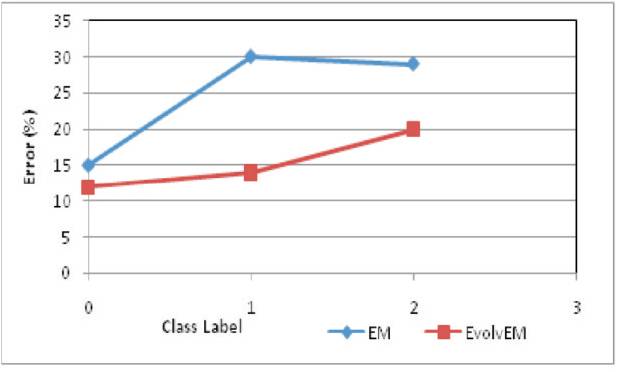
Comparison of EVOLVEM and EM Clustering When performing EM clustering, the clustering error rate is higher when compared to EvolvEM clustering as shown in Figure 1.

Figure 1.Comparison of EvolvEM and EM Clustering

Conclusion

The existing clustering methods do not provide optimal results. Also another problem that arises due to these clustering methods is that too many parameters are required to produce efficient outcome. In the proposed system, EM and the Genetic Algorithm(GA) are combined. The major advantage of this method is that it provides optimal result. Also only few parameters are needed for clustering. In EvolvEM clustering, the estimated expected values are maximized. But it will not produce optimal clustering. When EM is combined with GA, the mutation operation is used to produce efficient clustering. By using the fitness function, optimal clustering results and error rate is also reduced. As a future work, Bee Colony optimization algorithm can be combined with EM algorithm to perform better clustering.

References

[1]. Aleix M. Martinez, Jordi Vitria, (2000). "Learning mixture models using a genetic version of the EM algorithm," Pattern Recognition Letters, 21 (8), 759–769,

[2]. Charles Bouveyron, Stephane Girard and Cordelia Schmid, (2007). "High-dimensional data clustering," Computer Statistics Data Analysis, 52 (1), 502–519,

[3]. Dimitris Karlis, Anais Santourian, (2009). "Model- based clustering with non-elliptically contoured distributions," Statistical Computer, 19, 73–83.

[4]. Franz Pernkopf, Djamel Bouchaffra, (2005). "Geneticbased EM algorithm for learning Gaussian mixture models, "IEEE Transaction Pattern Analysis Machine Intelligence, 27, 1344–1348.

[5]. Kalyanmoy Deb, (2001). "Multi- Objective Optimization Using Evolutionary Algorithms," Wiley- Interscience series in systems and optimization, John Wiley & Sons.

[6]. Jeffrey L. Andrews, Paul D. McNicholas (2013), 'Using evolutionary algorithms for model-based clustering', Pattern Recognition Letters ,34 , 987–992 .

• E-Step: This step is responsible to estimate the probability of each element which belongs to each cluster P(C ,x ) Each element is composed by an attribute j k vector (X ) The relevance degree of the points of each k cluster is given by the likelihood of each element attribute in comparison with the attributes of the other elements of cluster Cj.
  [4]

  
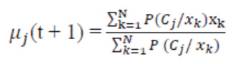
  • M-Step: This step is responsible to estimate the parameters of the probability distribution of each class for the next step. First, compute the mean (m) of class j j obtained through the mean of all points in function of the relevance degree of each point.