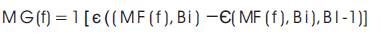
The Watershed transformation has recently become a popular tool for image segmentation. The purpose of image segmentation is to divide an original image into homogeneous regions. There exist several approaches to implement image segmentation. In this paper, Modified Multi-Scale Morphological Watershed Segmentation Algorithm of 2D Images Using Hill Climbing Techniques is introduced as a method of image segmentation. It is a fast and flexible algorithm for computing watersheds in digital grayscale images. A review of watersheds and related notion is first presented and the major methods to determine watersheds are discussed. The present algorithm is based on Hill Climbing process analogy, in which the flooding of the water in the picture is efficiently simulated using a queue of pixels. It is proved that the accuracy of this algorithm is superior to that of the existing implementations. In addition, its strongest point is that it is faster than any other watershed algorithm. Mainly it reduces the over – segmentation.
Image segmentation involves the partition of an image into a set of non-overlapping regions whose union is the entire image. Its main task is to decompose the image into parts that are meaningful with respect to a particular application. Among the existing algorithms [1–7], watershed transformation has proved to be a very useful and powerful tool in many different application fields. Watershed transform is commonly used in industrial, biomedical, and computer vision applications.
The idea of the watershed construction is quite simple. A gray scale image is considered as a topographic relief, the gray scale value of a pixel being the altitude at that particular point. Now, let a drop of water fall on such a topographical surface. By gravity, it will flow down along the steepest slope path until it reaches a point or region of minimum. The whole set of points of the surface, whose steepest slope path reaches a given minimum, constitutes the catchment basin associated with this minimum. Each pair of adjacent catchment basins are separated by watershed lines. Thus, raindrops falling on both sides of a watershed line flow into different catchment basins. The watershed transform has been approached from two different perspectives. One class of algorithms aims to detect the catchment basins by simulating the flooding process while the second tracks directly the watershed lines by using the arrowing techniques. Among these, there are algorithms which construct the watershed lines and the algorithms which do not delimit the basins by watersheds (0-width watershed lines).
The fast implementation of immersion-based watershed algorithm has been introduced by Vincent and Soille (1991). The authors simulated a flooding process, in which the water comes up out of the ground and floods the catchment basins without predetermining the regional minima. Alternatively, an ordered queue based watershed algorithm has been proposed by Meyer (1991). This algorithm determines the regional minima and starting from these minima, the recursive label propagation is performed using an ordered queue. It yields a complete tessellation of the image into its homogeneous regions without producing any watershed lines. Finally, several shortest-path algorithms for the watershed transformation with respect to topographical distance can be found.
Different algorithms have been proposed on standard sequential processors. Generally, dedicated hardware would respond faster than the software running on hardware of a general purpose processor. However, the complexity of hardware required to implement an algorithm depends to a large extent on the computational overhead of the algorithm to compute the watershed transform. Moga's algorithm [3], however, requires a lower complete transformation of an image, involving time-consuming multiplication by a constant of the gradient image based on geodesic distance. The present work improves upon Moga's algorithm by doing away with the lower complete transformation. Moreover, it develops and simulates a hardware architecture for implementing the proposed improved algorithm.
Modified Multi-Scale Morphological Watershed Segmentation Algorithm of 2D Images Using Hill Climbing Techniques is proposed here. In this algorithm there are five steps:
A segmentation algorithm can give better output without over-segmentation on a preprocessed noise free image. Images can get corrupted by additive impulse noise in the acquisition or transmission stages. These salt and pepper impulse corrupted pixel will tend to be a maximum or a minimum of any local window. In our older work we have proposed an Iterative Adaptive Switching Median Filter for the restoration of salt & pepper impulse corrupted images and is used here for the preprocessing of images to be segmented by our proposed segmentation algorithm.
A segmentation algorithm often needs a preprocessing step like noise smoothing to reduce the effects of undesired perturbation that might cause over and under segmentation. The very small- scale details are usually considered as noise. A Morphological opening is, that it is the union of all sets containing the structuring element in the original image. Both the opening and the closing operators have the effect of smoothing the image, with the opening operation removing pixels, and the closing operation adding pixels.
The local gray-level variation in the image can very well be given by the morphological gradient. A gradient helps detecting ramp edges and avoids thickening and merging of edges providing edge-enhancements. The gradient image, G(f) is morphologically obtained by subtracting the eroded image, from its dilated version. A multiscale gradient, MG(f) is the average of morphological gradients taken for different scales of the structure element, Bi.
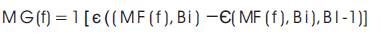
where Bi is a SE of size (2i+1) x (2i+1).
To avoid over-segmentation we find the multiscale gradient image. In this method the structuring element sizes are varied in each gradient image. N-number of gradient image are calculated and then added. Finally calculate the average of summation gradient image.
The Watershed segmentation algorithm applied directly to the gradient image can cause over-segmentation due to serious noise patches or other image irregularities. The concept of Markers can be used to solve this oversegmentation problem whose goal is to detect the presence of homogeneous regions from the image by a set of morphological simplifications. They spatially locate object and background, ensures to keep up the interior of the object as a whole. The Markers are connected components belonging to an image; internal markers are inside each of the objects of interest and external markers are contained within the back-ground.
Identify where the object is found we go for the Marker Techniques. In this method thresholding procedure is used. Fuzzy threshold is obtained manually then applied function of marker. If the current pixel gray value is less than the threshold then assigned the current pixel gray value is min value. Otherwise assigned the current pixel gray value is max value.
The original Hill Climbing Techniques are applied. In this techniques two different queues are used. First getting the current pixel gray value and 3 X 3 neighborhood pixel gray value. Check if the current pixel gray value is equal to neighborhood pixel gray value then assigns the currentlabel. Otherwise assign the current-distance. This process is repeated until all pixels gray values are verified. Once pixel verification is done then increment the current-label and current-distance value.
To reduce the over-segmentation applied the morphological opening and the closing functions. Then go for impose procedure. In this impose procedure watershed lines are merged to the original image.
Pseudo Code of Hill Climbing - based Watershed AlgorithmInput: Morphological multi-scale gradient image
Output: label image L and distance image
Initialize: INIT=-2; NARM=-1; DIST MIN=0; CURRENT LABEL=1;
Initialize the Label image L and the distance image d with INIT and MINDIST respectively;
For all p with L(p) = INIT
Do
CURR DISTANCE=1;
Initialize the queues Qpd and Qpa;
While queue Qpd not empty
Do
Dequeue the pixel q from the queue Qpd;
For all r ε N(q) {For all neighbors of q}
Do
If the gray value of r = gray value of q Then
Assign the CURRENT LABEL to L(r) and insert the pixel r into Qpd;
Else if the gray value of r < gray value of q Then
Assign the CURR DISTANCE to L(r) and enqueue the pixel q into the queue Qpa;
End if
End for
End while
Increment the CURR DISTANCE;
If queue Qpa is empty Then
Increment the CURRENT LABEL;
End If
End For
Figure 1 shows the system diagram of the proposed method. The contents of most of the boxes are covered in previous Chapters. Through the series of the process, the segmented image finally can be acquired. First of all, an image is read in and preprocessed by gradient operation applied separately to the input image for avoiding oversegmentation problem. The final result is segmented images are produced.
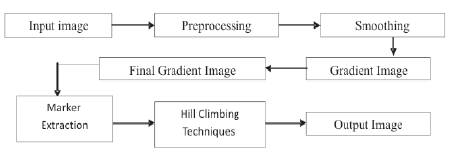
Figure 1. System diagram of the proposed method
The proposed algorithm has been implemented in IDL and applied on various test images to verify its effectiveness. To avoid over-segmentation, a gradient operation applied on an input for computing the watershed transformation. The gradient image is computed by using the multiscale morphological gradient operation. Sobel or other operations can be used as well, but the segmentation may be a little different.
A large variety of images both natural and synthetic images are employed in our experiment. Some segmentation results are shown in the following Figures. It is very obvious that the proposed approach is able to accurately locate the boundaries of the regions.
From the following figures, three columns of output is shown. First one is original image. Second one is output of Hill Climbing based Watershed image. Third column is output of the proposed algorithm.
Figures 2 to 10, nine images are shown for experiment results. First, Fruits. tif image of size 124 x 190. Second, Rice. tif image of size 256 x 256. Third image is Lena. tif of size 256 x 256.

Figure 2. Fruits - Original image

Figure 3. Fruits - Watershed Segmentation
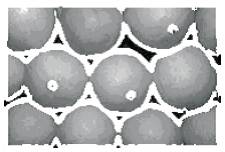
Figure 4. Fruits - Proposed Watershed Segmentation

Figure 5. Rice - Original image

Figure 6. Rice - Watershed Segmentation

Figure 7. Rice - Proposed Watershed Segmentation

Figure 8. Lena - Original image

Figure 9. Lena - Watershed Segmentation

Figure 10. Lena - Proposed Watershed Segmentation
The criteria of a good segmentation are,
The proposed algorithm has been tested for various test images to verify the effectiveness of the proposed algorithm. Some performance measures are evaluated and it is provided in the following Table 1.
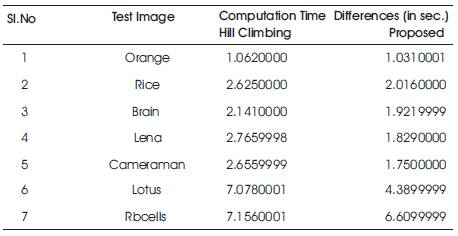
Table 1. Time Analysis (in sec.)
This paper presents Modified Multi-Scale Morphological Watershed Segmentation Algorithm of 2D Images Using Hill Climbing Techniques. This algorithm is extremely powerful compared to the existing ones. It is not a time consuming and also proves to be more accurate. The proposed method has a wide advantage over other methods in that it exactly provides the contour of the image, while other techniques require smoothing followed by region merging which is a tedious process. The effect of this segmentation algorithm can also be studied for recently generated wavelet transforms. Over Segmentations can be avoided by using most suitable preprocessing techniques like marker-control.