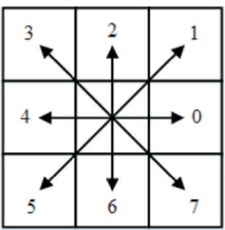
Figure 1. FCC with Eight Directions
Contour representation of binary object is widely used in pattern recognition. Chain codes are compression methods, where the original data are reconstructed from the compressed data for representing binary objects including contours. Though a notably huge image size reduction is obtained by fixed-length chain code, so far, more efficient and reliable methods for data encoding is possible by using technique that treats the binary bits differently considering its requirement of storage space, energy consumption, speed of execution, and so on. This paper proposes a new variant of Huffman Coding (HC) by taking into consideration the fact that the costs of bits are different, the new representation of the Freeman Chain Code (FCC) is based on an eight-direction scheme. An experimentation of the cost efficiency of the new representation over the classical FCC is described and compared to other techniques. The experiments yield that the proposed FCC representation reduces overall both the storage and the transmission cost of encoded data considerably compared to the classical FCC.
Most of object recognition techniques require the detection and the extraction of different object boundaries. Among those techniques, some applications also require to measure the geometric features of objects. Different encoding algorithms, e.g., Chain code, crack code, are available for contour tracing of binary objects and their encoding efficiency is very important in representing, recognising, transmitting, and storing the format of the objects.
In the recent years, application of battery-powered portable devices, e.g., laptop computers, Personal Digital Assistant (PDA), and mobile phones has increased significantly. The reliability and performance of such devices are primarily dependent on their power efficiency, i.e., effective battery life. Bigger battery size could help to improve power efficiency, however, in a portable device, the battery size is restricted by the size and weight of the device itself. Providing power to both portable and non-portable devices has led in significant interest in power reduction. As data (image) transmission is a common operation in both portable and nonportable devices, reduction of power dissipation in transmission systems is important.
In order to increase transmission speed and reduce power dissipation, parallel data transmission methods are widely used. However, parallel transmission is limited to short distance communications, e.g., locally connected devices, internal buses. Ruling out the possible availability of parallel transmission links over long distance, we are left with its serial alternative only. In image transmission, image compression techniques are widely used to reduce the size of image before transmitting the image over serial medium to reduce transmission time and cost.
Chain codes are widely used in pattern recognition and image processing for representing different rasterised shapes like lines, curves, or region boundaries. In 1961, Freeman proposed a novel method to represent the digital curves boundaries based on chain code (Freeman, 1961). In (Shih & Wong, 2001), the authors have presented an adaptive algorithm for converting the quadtree representation of binary image and a way of computing local symmetry of the contour of an object from its chain code representation was shown in (Shih & Wong, 1999).
Many authors have reported different interesting applications using chain codes in computer graphics (Globačnik & Žalik, 2010; Weng, Lin, Chang, & Sun, 2002; Nunes, Marqués, Pereira, & Gasull, 2000), image processing (Ren, Yang, & Sun, 2002; Ho, Chen, & Cheug, 2002; Arrebola & Sandoval, 2005), and pattern recognition (Kaygın & Bulut, 2001; Sun, Yang, & Ren, 2005; Putra & Sentosa, 2012). Each element in the code is built to show the relative angle difference between two adjacent pixels along the digital object’s boundary. In the eight-direction version of the FCC, the directions are represented as numbers from 0 to 7 (Figure 1) and the numbers are represented using 3 binary digits as 000, 001, 010, 011, 100, 101, 110, and 111, respectively.

Figure 1. FCC with Eight Directions
As a result, we require a number of bits equal to three times the number of total moves in all directions. Although, the chain codes reduce the size of the objects, they are not developed with the intention to produce efficient coding to minimise the number of bits required to encode the boundary of an object. Though the angle differences between two contiguous elements in a chain are not equally probable, i.e., frequency of movement in different directions are not same, the classical.
Freeman chain code does not take the frequency of movement in different directions into account while assigning codes. But encoding characters in predefined fixed-length code cannot achieve optimal performance, as every character consumes equal number of bits. A variable length encoding scheme can help to increase the compression performance of the chain code.
There are variable length encoding schemes like HC (Huffman, 1952) that considers the different discrete values probabilities are likely to occur and assign variable length code to symbols based on their occurrence frequencies, and thus represent a message with fewer number of bits. By utilising the compression performance of the HC, the chain code has been modified in (Liu & Žalik, 2005) in both classical and modified FCC. But in real life application, cost of letters are not always equal. For example, in Morse Code (MC), all the ASCII characters are encoded as sequence of dots (.) and dashes (-), where a dash is three times longer than a dot in duration (Redmond, 1964). However, the MC scheme suffers from the prefix problem (Nunes et al., 2000). Ignoring the prefix problem, MC results in a tremendous savings of bits over ASCII representation. Using MC, we can treat the binary bits differently; 0 as a dot and 1 as a dash.
Therefore, if the bit costs are unequal then length and cost of code words are different. Using compression techniques without taking into consideration, the fact that bits can be with different costs may help to reduce the number of bits to represent a message, but may not be able to reduce the cost of the message. A number of researchers like (Altenkamp & Mehlhorn, 1980; Perl, Garey, & Even, 1975; Gilbert, 1995; Golin, Kenyon, & Young, 2002) have proposed data compression techniques that consider unequal letter costs. This paper extends the work presented in (Kabir, Azad, & Alam, 2014) to introduce a novel representation of the classical FCC considering the costs of binary bits as unequal. These experiments suggest that the technique contributes towards improved performance and it reduces the overall requirements of resources considerably. This technique also reduces cost by 3.75% in the worst case scenario; in the best case it reduces cost by 22.69%, and on an average by 10.78%. A comparison among the cost of Classical FCC, FCC using HC technique and the proposed representation using HC with unequal letter costs is evaluated and the result is presented.
FCC is the most widely used chain code technique because of its simplicity. This coding technique encodes an object as a sequence of moves through the neighbouring boundary pixels based on eight-connectivity. The direction of moves in the chain is encoded by using the numbering scheme {i|i = 0, 1, 2, . . . , 7} that is denoting a counter-clockwise angle of 45°×i with respect to the positive x−axis, as shown in Figure 1. This scheme is also known as Freeman Eight-Directional Chain Code (FEDCC). In Figure 2(b) the eight-directional chain is shown for the shape as shown in Figure 2(a). The four-directional version of chain code (FFDCC) is also used where direction of move is encoded using a numbering scheme {i|i = 0, 1, 2, 3} denoting an angle of 90°× i counter-clockwise with regards to the positive x-axis. In classical FCC, the chances of move towards different directions are not equiprobable. The probability of angle differences between two contiguous elements in a chain code is shown in Table 1.
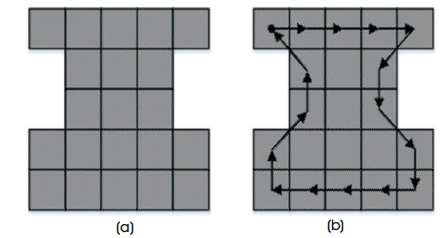
Figure 2. Example of FCC (a) Example Image, (b) Chain Representation of the Image

Table 1. Probabilities of Angle Differences between Contiguous Segments (Liu & Žalik, 2005)
Angle differences between neighbouring pixels vary from object to object. It is seen from Table 1 that the probability of the next move is the highest (0.488) at 45° and 315° and is the lowest (0.003) at 180° from the present position. The observation suggests that movement at 45° or 315° is the most frequent and at 180° is the least frequent. But FCC does not consider the changes in frequency of movement during assigning code to the elements of a chain. Classical FCC assigns three bits of predefined fixed length code to each of the elements in the chain. By considering the frequency of movement, a new representation of FCC in proposed in (Liu & Žalik, 2005). However, this is not the only modified representation of FCC. Bribiesca represented shapes using a derivative of FCC in 1991 (Bribiesca, 1992). He also proposed another representation of chain code known as Vertex Chain Code in 1999 (Bribiesca, 1999). Different modifications of FCCs are described in (Bribiesca, 1999; Liu, Wei, Wang, & Žalik, 2007; Priyadarshini & Sahoo, 2011; Liu, Žalik, Wang, & Podgorelec, 2012; Žalik & Lukač, 2014).
An important function of a digital communications system is to represent the digitised signal with as fewer bits as possible without losing information. However, in several applications involving image processing and sound representation, certain degree of information loss may be acceptable as it does not invalidate the purpose of those applications. Data must be encoded to meet the purposes like: unambiguous retrieval of information, efficient storage, efficient transmission, and so on. Efficiency can be measured in terms of incurred cost, required storage space, consumed power, time spent, and likewise. Let a message consist of sequences of characters taken from an alphabet Σ, where α1, α2, α3 ..., αr are the elements that represent the letters in the source Σ. The length of α represents its cost or transmission time, i.e., ci = length(αi). A codeword wi is a string of characters in Σ, i.e., wi ϵΣ+. If a codeword w = αi1, αi2,..., αin, then the length or cost of the codeword is the sum of the lengths of its constituent letters:
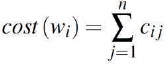
A scheme of prefix code assigns codes to letters in Σ to form code word w such that none of them is a prefix to i another. For example, the code words {1,01,001,0001} and {000,001,011,111} are prefix-free, whereas the code words {1,01,100} is not, because 1 is a prefix in 100. Prefix-free property is very desirable to be able to uniquely decipher a code. The problem of constructing an optimal prefix code when all the letters of the alphabet are of equal cost and the probabilities of the words are arbitrarily specified was solved by Huffman (Huffman, 1952). But the letters in the alphabet may require unequal cost. For example, in MC a dash (-) is three times longer than a dot (.) in duration (Redmond, 1964). MC is an example of a variable- length encoding scheme.
In MC, frequently used letters like E and T have shorter length codes than seldom-used letters like Q and Z , which have longer codes. Using MC, we can treat each dot and dash mark as the equivalent of one binary bit each. The more general case where the costs of the letters as well as the probabilities of the words are arbitrarily specified was treated by Karp (1961). A number of other researchers have focused on uniform sources and developed algorithm for the unequal letter costs encoding (Krause, 1962; Varn, 1971; Cot, 1978; Altenkamp & Mehlhorn, 1980; Perl et al., 1975; Gilbert, 1995). Let p1, p2,..., pn be the probabilities with which the source symbols occur in a message and the codewords representing the source symbols are w1, w2,..., wn then the cost of the code W is,
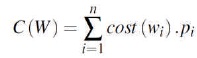
The aim of producing an optimal code problem with unequal letter cost is to find a codeword W that consists of n prefix code letters each with minimum cost ci that produces the overall minimum cost C(W), given that costs 0 < c1 ≤ c2 ≤ c2 ... ≤ cn, and probabilities p1≥ p2 ≥ . . . ≥ pn > 0.
Technique of producing HCs is an optimal encoding rule that minimises the number of bits needed to represent source data was proposed by Huffman (1952). It is an entropy encoding algorithm used for lossless data compression. It is an efficient data compression scheme that takes into account the probabilities at which different quantisation levels are likely to occur and results into fewer data bits on the average. For any given set of levels and associated probabilities, there is an optimal encoding rule that minimises the number of bits needed to represent the source. Encoding characters in predefined fixed length code does not attain an optimum performance because every character consumes equal number of bits. HC tackles this by generating variable length codes, given a probability usage frequency for a set of symbols. The classical HC requires to pass the input data two times to complete the encoding operation. In the first pass, it reads the whole stream to determine the occurrence frequencies of distinct symbols. After that symbols along with their frequencies are used to generate a binary tree known as Huffman tree. The process of Huffman tree generation is shown in algorithm 1 (Cormen, Stein, Rivest, & Leiserson, 2001).
In the algorithm 1, C is the set of n distinct symbols, and each symbol c ϵ C has a frequency denoted as f [c]. The algorithm starts its operation with a set of |C| leaf nodes, where each node corresponds to a distinct symbol. After that a sequence of |C|-1 merging operation is performed to obtain the final tree. The merging is done by extracting two least frequent symbols from the minimum priority queue, Q, and creating and inserting a new node (parent) to the queue for that two symbols. These two symbols are considered as the left and right child of their parent node, respectively. The frequency of the new node is calculated as the sum of the frequency of its child nodes. The resultant tree ensures the optimal encoding of symbols to obtain maximal compression performance.

To form a codeword for a symbol, the tree is traversed from the root to the leaf node representing the symbol. In the traversal process, any move made towards the left direction is replaced by '0' and any move towards the right direction is replaced by '1'. As a result, codeword for each symbol consist of a sequence of 0's and/or 1's. Once the codewords are obtained, in the second pass, the Huffman algorithm encodes the symbols of the input message with the codewords, thus reducing the size of the whole message.
Applications of HC are pervasive throughout computer science. Researchers proposed different variants of HC that compress source data to reduce data size and/or transmission cost. For example, Mannan and Kaykobad introduced block technique in HC, which overcomes the limitation of reading whole message prior to encoding (Mannanand & Kaykobad, 2003). In classical HC scheme, the letter costs are considered as equal. The unequal letter cost versions of HCs scheme are proposed in (Golin & Young, 1996; Golin et al., 2002; Bradford, Golin, Larmore, & Rytter, 2002; Golin, Mathieu, & Young, 2012). In the unequal letter cost version of the classical HC, letters of the alphabet are considered as unequal. Recently, in (Kabir, Azad, Alam, & Kaykobad, 2014), a method was proposed to show the effects of unequal bits cost on classical HC. The idea of this method is to assign the most frequent symbol the minimum cost and the least frequent symbol the maximum cost code, whereas classical HC assigns most frequent symbol the minimum length and the least frequent symbol the maximum length code. As a result, their approach produced an optimal prefix-codes for unequal letter cost, thus reducing the overall (transmission) cost of the encoded data. It is worth noting that while considering letter or bit cost as unequal, the length and cost of a codeword is not the same. For example, if we consider cost of the binary bit 1 as three times that of the cost of binary bit 0 (analogous to dash ( ) and dot (.) in MC), then codeword 011 has length 3, but cost 7 (considering cost of '0' as 1 and '1' as 3 unit).
For example, Table 2 shows six different symbols, their frequencies, and the codewords generated for those symbols using both classical HC and HC with unequal letter costs. The trees generated by classical HC and HC with unequal letter costs are shown in Figures 3 and 4, respectively.
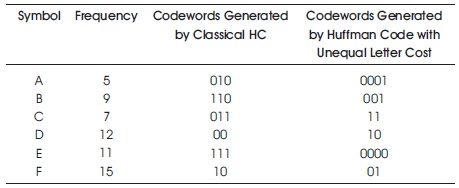
Table 2. Codeword Generated by Variants of HC
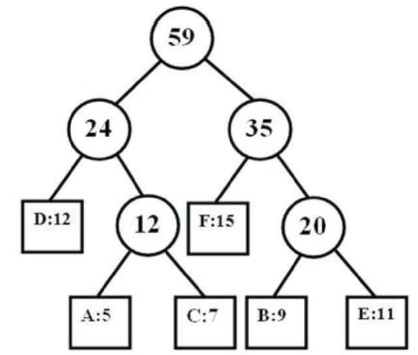
Figure 3. Tree Generated by Classical HC
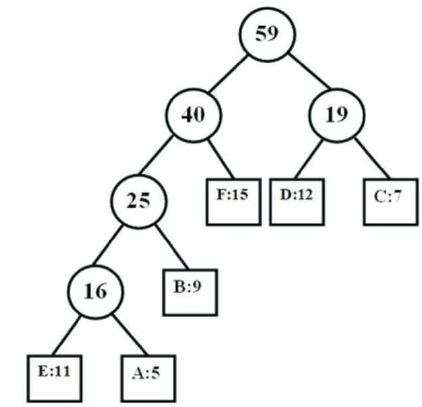
Figure 4. Tree Generated by HC with Unequal Bit Cost
HC technique is an optimal encoding scheme that achieves the minimum amount of redundancy possible in a fixed set of variable-length codes. Its application reduces the average code length used to represent the symbols of the source alphabet. As FCC is a fixed-length coding scheme and does not take the frequencies of movements in different directions into account, application of this scheme results in more number of bits to encode an object. HC scheme could be used to help considering frequencies of moves in different directions in FCC, and thus reducing the total number of bits. The uniquely decodable variable-length codes to denote different moves in the chain code is obtained by using the HC technique. The process of using HC to compress FCC is shown in Figure 5.

Figure 5. Process of Representing FCC using Classical HC
In the first step, the input image is provided to the chain code generator block. The chain code generator obtains the chain code representation of the contour of the image using existing chain code generation algorithm. In addition to the coordinate of the starting pixel of the chain code and the code itself, i.e., sequences of moves, this block also counts the number of moves in different distinct directions. The number of moves in different directions along with the moves themselves are then fed to the HC generator. It treats each move as a distinct symbol and number of occurrence of each move in the chain code as their frequency. Based on these data and using the HC algorithm (Algorithm 1), variable length codeword is generated for each move. In the next step, the codewords are assigned to their respective moves to have a new representation of the moves in the chain code. In the new representation, moves are denoted using variable length codewords, however, the sequences of moves in the chain code are not altered. In this way, a compressed representation of the chain code is obtained.
Table 3 shows the frequencies of angle changes in the chain representing the butterfly image of Figure 6 and also shows the fixed-length code assigned by classical FCC and the variable-length code assigned by the HC. To encode the chain of the butterfly image, the classical FCC takes 2751 bits, on the other hand, FCC with HC takes 2684 bits. At the same time, cost (length) of the FCC is 5705 unit and cost of the FCC using HC is 5634 unit for the butterfly image by considering the cost of binary bit '1' as 3 unit and cost of bit '0' as 1 unit (analogous to '−' and '·' of MC).
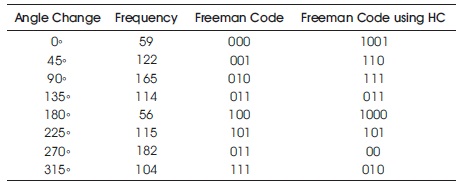
Table 3. Codewords Assigned by FCC and FCC using HC

Figure 6. Example Image
In the above section, it is seen that the HC could be used to compress the FCC. Classical FCC assigns fixed-length codewords and HC technique assigns variable-length codewords to represent moves in different directions, but none of the techniques take unequal bit costs into account while assigning codes. But in section 1.2, we have seen that a considerable amount of research has been performed to address the issue of unequal bit cost problem. Therefore, if the aim of data encoding is to reduce the overall cost instead of number of bits, then it requires to consider unequal letter/bit cost during the encoding process. As described earlier, different versions of the HC with unequal letter cost is available in the literature. But representation of the FCC with unequal letter/bit cost has not been considered. A new representation of FCC with unequal bit cost is possible that can be considered analogous to HC with unequal letter cost. The process of using unequal letter cost variant of HC in representing FCC is shown in Figure 7.
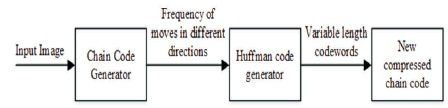
Figure 7: Process of Representing FCC using Unequal Bit Costs
In the first step, the input image is provided to the chain code generator block. In this block, chain code of the image is generated using the FCC scheme. In addition to the chain of the contour of the image, the total number of moves in different directions are counted. The number of moves in different directions along with the moves themselves are then given as input to Algorithm 2. After performing different operations, the algorithm returns a binary tree (a set of codewords). The process of creating the binary tree starts with a single node (root node) and it is initialised with cost 0. After that two child (leaf) nodes are created for the root node, i.e., level of the tree is increased by one. Cost of the left child is calculated as the summation of the cost of its parent node and the length of the left arc, and cost of the right child is calculated as the summation of the cost of its parent node and the length of the right arc. Length of left and right arcs are actually the cost (length) of 0 (a) and 1 (b), respectively. The next step is to take a child node with least cost and create two child nodes for it and make it a parent node. In this way, in every iteration, the child node with least cost becomes a parent node with two new child nodes. Creation of new child nodes is stopped when total number of child nodes become equal to the number of distinct moves (8 in this case) needed to be encoded.
Now the tree T is constructed and the cost of the tree actually depends on how the frequencies are assigned to the leaf nodes. The overall cost will be minimised if the leaves with highest cost always have smaller or equal weight (frequency). To fulfil this condition, the leaves of the T are enumerated in non-decreasing order of their cost, i.e., cost(l1) ≤ cost(l2) ≤ . . . ≤ cost(ln), and that f1 ≥ f2 ≥... ≥fn, where li and fi are leaf nodes and frequencies of distinct triplets, respectively for i = 1, 2,..., n. The frequency or weight of parent nodes are calculated as the sum of the frequencies of its child nodes, and it continues upwards until the root node is reached. After that the algorithm checks for any possible conflicts between all pair of nodes. Two nodes are considered as conflicted if the node with a higher cost has higher frequency violating the above condition, i.e., if cost(li) > cost(lj) and f(li) > f(lj), then there remains a conflict. If there remains a conflict between nodes, then it is resolved by swapping the nodes and recalculating the cost of the tree downward and frequency of the nodes upward. When all the conflicts if existed are resolved then the algorithm generates codewords for each of the distinct moves.

In the final step, the code-words are assigned respectively to their moves to have a new coding of the moves in the chain code. In the new representation, each move is given using variable length codewords which are obtained by treating the binary bits unequally. The process is illustrated by applying it to an example image as shown in Figure 6. The resultant codewords of the new representation for the butterfly image of Figure 6 is shown in Table 4. For this particular image, the most frequent move is in 270° and the least frequent is in 180° angle. Therefore, the new representation assigns the least costly code (0000) to represent a move in 270° and the most costly code (101) to represent a move in 180°. A comparison between cost and bits required by the classical FCC, FCC using HC, and FCC using HC with unequal bit costs to represent the chain of the butterfly image is shown in Figures 8(a) and 8(b) respectively. In terms of cost, it is seen from Figure 8(a) that the new representation of FCC using HC unequal bit cost incurs the least cost to encode the chain, whereas classical FCC incurs the most cost. The cost (length) incurred in the FCC is 5705 unit and the cost incurred in the new coding is 4851 unit. As a result, the cost improvement by the new coding is 14.97%. However, the new representation with different bit cost takes more bits than other two coding methods and the other method using classical HC takes the fewest number of bits.

Table 4. Codeword Assigned by FCC and FCC using HC with Unequal Bit Cost
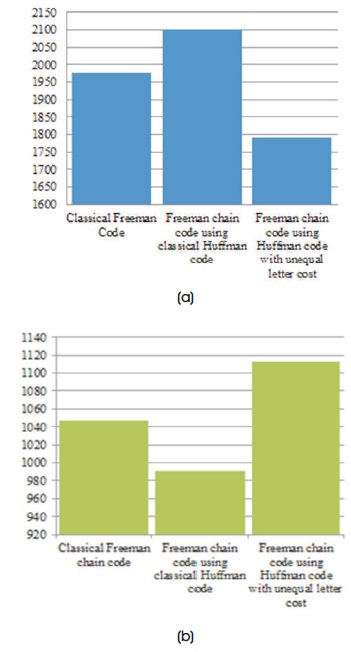
Figure 8. Comparison among Different Variants of FCC
FCC technique does not consider the frequency of angle differences between two contiguous elements in its algorithm and assigns three bits fixed-length codes to represent movements in different directions. On the other hand, HC technique considers frequency of the symbols that are contributing to the data. It aims to increase the compression rate based on the frequency of occurrence without considering the bit costs, i.e., most frequent symbols are given shortest length codes and vice versa. It is possible to compress FCC using HC as seen in the example of above section. The new representation of the FCC takes cost of bits contributing to the codewords of the symbols into account. As a result, total cost of the compressed data is reduced as most frequent move in a certain direction contributes relatively less to the cost of compressed data with compared to the both classical FCC and FCC using HC.
To evaluate the performance of the new representation of the chain code, experiments were performed on 110 images of arbitrary shapes. The author has analysed the experimental data such as cost of compressed data and bits required by three different representations of the FCC.
Figure 9 shows sixteen of the test images. For each of those images, chain codes were generated and variable-length codewords were generated by using the classical HC and the HC with unequal bit cost algorithm. Cost incurred in the classical chain code and the new representation of the chain code to encode the contour of the images of Figure 9 along with the total number of moves in the chain and the percentage of cost improvement by the new representation for each of those images are shown in Table 6. From Table 6, it is seen that the horse image (Figure 9n) has the maximum number of moves in its chain and the penguin image (Figure 9i) has the minimum number of moves in its chain.

Figure 9. Sixteen Test Images (a) Butterfly (b) Banana (c) Man (d) Ostrich (e) Cow (f) Deer (g) Bear (h) Eagle (i) Bird (j) Fish (k) Fox (l) Penguin (m) Panther (n) Horse (o) Giraffe (p) Elephant
The experimental results for all 110 images are shown in Table 5, Figures 10 and 11. Figure 10 shows the cost comparison among different representations of the FCC in representing different images. It is seen from this figure that for every image, the new representation of the FCC with unequal bit cost incurs least cost. These experiments suggest that the technique reduces cost by 3.75% in the worst case scenario; in the best case it reduces cost by 22.69%, and on an average by 10.78%. A mixed trends is seen between the cost of classical FCC and FCC using HC. For some images, the former performs better and for some other images, the later one performs better. But in terms of cost reduction, the new representation considering unequal bit cost outperforms other two representations of the chain code. With regards to bits requirement to represent the chains, the representation of FCC using HC technique performs better than the other two representations as seen in Figure 11.
Table 5. Trends of Moves in Different Directions and Cost Improvement by the New Representation for Images with Different Ranges of Moves
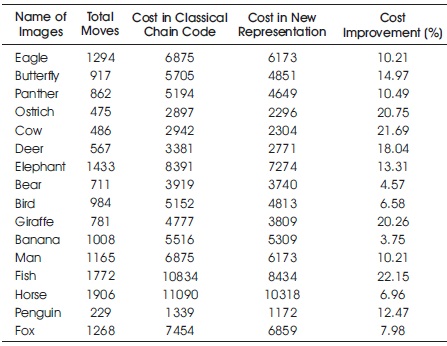
Table 6. Performance of the New Representation of the Chain Code for the Sixteen Test Images
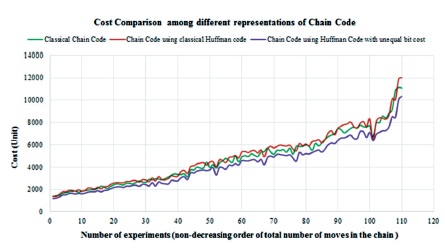
Figure 10. Cost Comparison among Different Representations of FCC
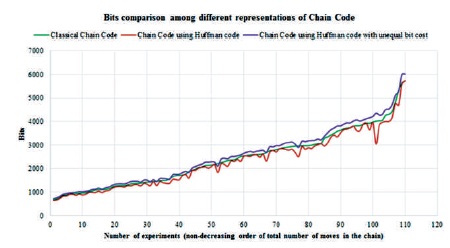
Figure 11. Bits Comparison among Different Representations of FCC
As the images are of different dimensions and shapes, a varied number of total moves in different directions are required to represent the boundary of the images. A varying trend is seen in the percentage of moves in each of the eight directions with the varying number of total moves (see Table 5). As seen from Table 5, the best average cost improvement is obtained for those images for which the total number of moves in the chain code is in between 1401 and above, whereas the least average cost improvement is obtained for the images having the total number of moves in the range between 1201 to 1400. It is also seen from Table 6 that the maximum cost improvement is obtained for the fish image (Figure 9j) although it does not have the maximum number of moves and the least cost improvement is obtained for the banana image (Figure 9b) although it does not have the minimum number of moves. It is also seen from Table 6 that a relatively good cost improvement is obtained for the ostrich and the cow image (20.75% and 21.69%, respectively) although these images have relatively less number of total moves in their chain, on the other hand, relatively less cost improvement is obtained for the horse image although it has the maximum number of moves in its chain. By observing the trends of cost improvement from Tables 5 and 6, it can be said that the cost reduction is not dependent on the total number of moves, rather it depends on the shapes of the images, i.e., relative angle difference between the border pixels of the images. If the chain code of the contour of an image is dominated by the moves in some certain directions, then due to the nature of the Algorithm 2, a better cost improvement is obtained. Because, in such situations, moves in some special directions are most frequent therefore they are given the least cost code, and thus they contribute relatively less in the total cost with compared to the least frequent moves.
The encoding efficiency to represent shapes of objects is very important in digital object recognition and analysis. FCC, a fixed-length encoding scheme, is an efficient lossless compression method for representing binary objects and contours. Encoding symbols using predefined fixed-length FCC does not attain an optimum performance in terms of compression because every symbols consumes equal number of bits.
Statistical analysis shows that the moves in different directions in the chain code are not equiprobable, therefore variable-length codes are selected as a potential solution to increase the compression performance of the chain code. Representing FCC using HC helps to attain an optimum compression performance because HC assigns variable-length code to symbols based on their occurrence frequency. All these methods consider the costs of binary bits constituting the codewords as equal, thus consider the length of codeword of the elements in an Σ only and do not consider the cost of bits creating the codewords. As a result, even though it might achieve a high compression ratio, it incurs a high cost as well.
In order to evaluate the effects of unequal bit costs on the FCC, in this paper, the author proposes a new representation of the FCC using HC with unequal bit cost. The proposed approach considers the binary bits costs as unequal and assigns variable-length codewords to denote moves in different directions. The new approach assigns least costly codeword to the most frequent moves and vice versa. Consequently, the overall cost is reduced as the most frequent symbols contribute more to the uncompressed data. The effectiveness of the proposed approach is evaluated by applying it to several images with different shapes and sizes. The performance of the approach has been compared with the performance of the classical FCC and the FCC using the classical HC. The comparison of cost requirements among the classical FCC, chain code with HC, and the proposed representation of the chain code confirms that the proposed method requires minimum cost to represent the object contour among all different representations. However, in terms of compression performance, the FCC with the classical HC per forms better than other two representations. Therefore, users can make a tradeoff between cost and compression ratio by choosing a suitable representations of the FCC. In one hand, representation of FCC using classical HC would attain good compression performance, on the other hand, FCC using unequal bit cost would produce cost efficient representation. At present, we do not consider the switching activities in the codewords, which has a linear relation with the power consumption. In future, we hope to extend this work by reducing the number of switching activities in and between the codewords to further reduce the cost of transmission.
I would like to take this opportunity to express my profound gratitude and deep regard to Dr. Sohag Kabir from the university of Hull, for his help throughout the duration of this work.