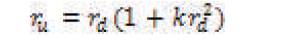
Most of the embedded products designed today are Vision-based systems with camera as a main component for its implementation. The cameras with wide angle lens enable them to capture images giving high-level descriptions of the scene useful for several applications, such as video surveillance, motion analysis, human/object detection, etc. However, images obtained using these wide angle lenses tend to be distorted causing straight lines from the scene to appear as curves in the image plane termed to be as Barrel or Radial Lens Distortion. Such distortion produces less realistic images and affects objects relative sizes, depending on their position in the image. It may be still acceptable in fisheye images, but in fisheye videos, the resulting distortion renders them hard to understand and uncomfortable to watch. It is therefore desirable to correct the barrel distorted images/video before presenting to the end viewer. A lot of research on algorithm that corrects for the distortion of the lens has been done to resolve this problem of radial distortion. Implementing this correction algorithm on a hardware platform can help in developing an ASIC that could be embedded into these Vision-based systems. In this paper, the authors review a framework to correct a wide angle lens distortion based on rectilinear and polynomial based model. The MATLAB implementation of these Distortion correction algorithms is done and comparison of their result is made. It is observed that rectilinear model gives efficient results as compared to polynomial based approach. The hardware platforms used to implement these algorithms are also been discussed. The analysis of these platforms suggest the advanced FPGAs (Field Programmable Gate Arrays) with embedded DSP blocks as a good choice for implementing these Barrel distortion correction algorithms for real time video capturing systems using wide angle lenses making it distortion free.
The necessity of camera in industrial automation is increasing. The image processing technology has enabled the development of smarter systems using camera as their main component. Actually, it's the rear view or wide angle lens cameras that are being used in video surveillance, Computer vision system, robotic vision, Motion tracking, automotive rear-view imaging systems, etc. However, performance of these systems depends on the quality of image captured through the camera. Wide angle lens of this rear view camera allows capturing a larger coverage area into a single image. This wide-angle image provides a vivid visual impression of a scene. The camera lens used to capture these wide angle images makes the real world scene look different from the way human would perceive, i.e. when we see the world with our eyes; we experience a wide field of view without any obvious distortion. The objects in the scene tend to retain their natural shape and structures making them appear to be straight. Although sometimes it's quite challenging to create flat image of such wider view that could match our subjective perception. The area covered by the wide angle lens from a certain view point can appear to be as sphere drawn from a view point as centre. The transformation of this sphere into an image plane however causes image to be unnaturally stretched and curved. This kind of distortion is therefore known as Barrel or geometric distortion which affects the quality of image captured lowering the performance of this camera based systems. It can be observed that this distortion is a result of inherent property of lens capturing wider field of view. Figure 1 shows an example of images captured with wide angle lens.

Figure 1. Examples of Images taken with Wide Angle Lens
The security and safety are one of the major concerns for the society. Application like Video Surveillance systems is found to be significant in contributing to its safety factor. It is used as a security system because of its ability to detect and track a particular object in motion. This tracking needs to be accurate and robust. For example in case of the military applications, a video surveillance is used to develop a sensor network, monitoring larger range of field on each sensor node for detecting intruders or tracking a moving object. However, the wide angle cameras used in capturing this larger view introduces a strong lens distortion making scenario both unusual and confusing to the viewer. Since detection of intruders or objects plays an important role under such application, the resulting distortion misleads the exact coordinates where motion of object is being sensed. It produces less realistic images and affects the object’s relative sizes, depending on their position in the image. Hence accuracy of the system is lowered. A solution to this problem is to incorporate the distortion correction algorithms to obtain most accurate position of motion.
Recent techniques for capturing and automatically stitching together multiple images of a scene have enabled photographers at all skill levels to produce high resolution wide field of view panoramas. At times it may be impossible to move the camera far enough away from the subject of interest to use a lens with a narrower field of view. Cartographers have long recognized that mapping a sphere to plane is difficult and lot of projection models has been developed over the years. Artists have also developed specialized techniques for handling large fields of view. Methods based on geometric correction have been proposed. The algorithms that corrects for the distortion of the lens has been developed to resolve this problem of radial distortion [[1] , 3, 5, 6, 8, 10,12]. The parallel grid structure is mostly considered as a base for correction. Couple of research works used complete information from the images for distortion correction [9, 11]. The distortion in image is calculated from the feature present in the image, but the results were just acceptable [2] and uses grid pattern to calculate the correction factor. The distinctive curvilinear perspective generated by fisheye (wide-angle) lenses may be desirable in fisheye images. However, in case of videos the resulting distortion makes it inconvenient and difficult to perceive, especially when it changes from frame to frame. The approaches studied above use some features in the image frame to correct the lens distortion. This helps to determine the correction factor for the particular system, but at the same time increases time complexity of algorithm. Along with time complexity, processing a video specifically in real time demands larger space and faster computation in order to have an uninterrupted view. Thus implementing distortion correction methods on an efficient hardware also becomes necessary.
The previous approaches studied in literature can be categorized into polynomial or non-polynomial based methods. The fisheye radial distortion model [3, 10], division distortion model [8] can be described as polynomial based method whereas rectilinear model as non-polynomial based approach. These algorithms have been verified by researchers using either software or hardware techniques. For real time system, hardware approach is more convenient and could be easily embedded for several applications. It is therefore also necessary to understand various hardware platforms suitable for implementation.
This paper thus aims in reviewing the existing Barrel distortion correction algorithms and their hardware implementation in order to identify most suitable approach to overcome this Lens distortion problem for smart camera systems.
Mathematically, the barrel distortion increases as the square of the distance from the centre and can be modeled in different ways. The Lens Correction algorithm therefore defines the relation between radial distance to distorted point (rd) in real time image and to undistorted point (ru) from the image centre. Figure 2 shows Barrel Distortion Model. Among the several approaches, two commonly used approaches that describes this relation is polynomial based approach or non-polynomial based approach using a rectilinear or perspective model. These approaches as implemented in [1] and [5] are described as below:
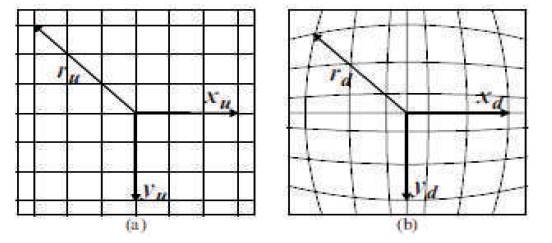
Figure 2. Barrel Distortion Model
The Barrel distortion causes a greater magnification at center of image than at edges and making all points in image to move radially towards the center. Thus distortion model is given as,
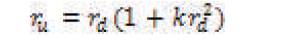
However, this correction model has been defined in terms of the distorted image, i.e. the position of the pixel in the distorted image is used to calculate where the pixel should be stored in a corrected image. Thus, in order to perform real time correction necessary to produce the undistorted output pixels in raster order; the model was redefined in [5] by letting the coordinates in undistorted image to determine which pixel in the distorted image should be displayed.
Hence the equation (1) is modified in form of,
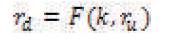
where ru is calculated as,
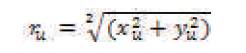
Equation (2) can be written in terms of radial dependent magnification as,
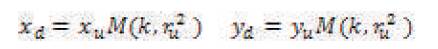
where M(k, ru2 ) = M is a magnification factor that depends on the distortion and position in the image given as,
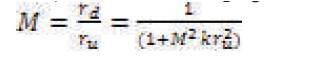
The above magnification factor provides mapping of distorted pixels in undistorted image location thus correcting the distorted image.
A perspective model is developed that represents a projection function of certain lenses as shown in Figure 3. According to this model, the radial distance from the Principal point (the centre of the image) to the Image point depends on the incoming angle 'θ' measured from the lens axis and on the projection theta (θ) is the deviation angle. Hence θ is used as reference factor to determine the shift of pixel location in distorted image. The calculated displacement using theta is then used to correct the image by restoring the pixels at its original location.
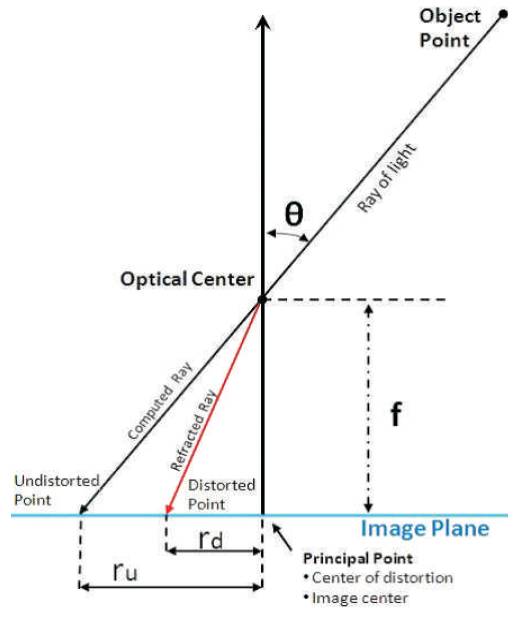
Figure 3. Image Projection
The algorithm first calculates value of θ as,
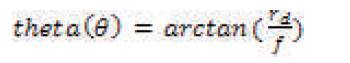
It is found that the lens distortion varies with the focal length of camera and the quality of the camera lens used in the system [1]. Hence corrected distance as defined in [1] is,
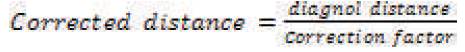
where, Correction factor is the input parameter to the algorithm and varies from lens to lens.
The authors have implemented both the algorithms described in Section 1.1 in MATLAB. The results obtained from both these approach is shown in Figure 4 and Figure 5. Input is a Barrel distorted raster image of size 293 x 408. It is observed that MATLAB results of Algorithm-1 (Section 1.1) for k=5.5 and k=5.8 appears to be similar to MATLAB results of Algorithm-2 (Section 1.2) for k = 2.4 and k = 2.5, respectively except that near upper edges. More loss is observed in Algorithm-1 as compared to Algorithm-2.
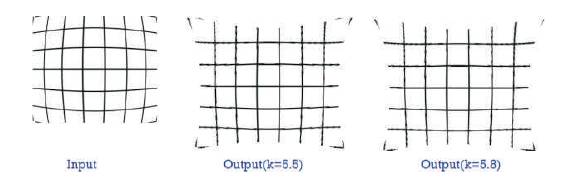
Figure 4. MATLAB results for Algorithm -1 (Polynomial Based Model)
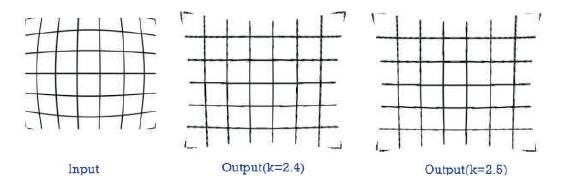
Figure 5. MATLAB Results for Algorithm -2 (Rectilinear Model)
Lens correction algorithm includes complex mathematical functions and hence would require larger time to execute. Also it is still acceptable for Barrel Distorted images, but in case of Distorted Videos, it requires large space as well complex processing for correction. Thus, in order to reduce the execution time of algorithm, the correction algorithm should be smartly implemented onto hardware with real time processing capabilities [1]. Lens distortion correction has been implemented along with Motion tracking system on Blackfin processor, BF-561, as its architecture is specifically designed for image processing application. The various resources like dual core processor, internal memory and direct memory access proved it to be useful in meeting the real time constrains in algorithm implementation [5]. The polynomial based radial distortion model was successfully implemented on RC100 development board with Spartan II FPGA as the main chip. The implementation shows the use of half the Logical resources of the device and suggested its implementation to be performed on higher end FPGAs such as Virtex versions with embedded multipliers and DSP blocks to reduce the resource utilization. The research work in [4] presented the implementation, optimization, and characterization of a fisheye lens distortion correction application on three platforms: a conventional, homogeneous Multicore processor by Intel, a heterogeneous Multicore (Cell BE), and an FPGA. However, among the three platforms used, the authors have concluded that FPGAs could be advantageous in meeting the expectations of performance, flexibility, and low overhead providing real time processing speed for Distortion correction on hardware.
The Barrel distortion correction algorithms reviewed in this paper successfully corrects the Distortion for image as well as video. The slight difference as observed in their MATLAB results is loss of information at edges for correction algorithm in [5]. Also due to availability of both low-cost and high-end DSP-optimized Field Programmable Gate Arrays (FPGA) devices, extensive IP cores, hardware accelerators, and softcore processors with design flexibility FPGA could be a good choice as a hardware architecture for implementing Distortion Correction algorithm for real time video capturing systems with minimum Barrel distortion for wide angle Lens systems. However for all the implementation found in literature, the correction is defined only based on visual abilities and no standard comparison parameter is defined. Hence it is important to compare the image before distortion and after correction using some parameters.
It has been observed through MATLAB, a rectilinear model could give a better correction out of two approaches implemented. Comparison of other models can be also be done in MATLAB and MATLAB functions such as PSNR or SSIM (Structural Similarity Index) can be used to compare their results and also to determine proper value of correction factor by comparing the corrected outputs with different value of correction factors with standard undistorted output. Also implementing these correction algorithms dynamically on advanced versions of FPGA, such as Virtex 5, 7 or on SoC like Zync platform can significantly improve the processing time and resource utilization to be able to develop an ASIC that could be used in such Vision based systems using a Wide angle Lens.