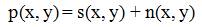
This paper introduces bivariate thresholding based Dual Tree Complex Wavelet Transform (DTCWT) technique to remove both Gaussian and speckle noise signals. Since both types of noises are different in nature hence it is difficult to remove them by using single filter. In this paper DTCWT approach is used to denoise ultrasound images. DTCWT based filter removes Additive White Gaussian Noise (AWGN) effectively. Since speckle noise is multiplicative in nature; it is converted into logarithmic transform before applying wavelet transform. Bivariate shrinkage (soft thresholding) function is used.
Many noise reduction techniques have been developed for removing noise and retaining details in different types of images. Medical imaging [1,2] is widely used to diagnose the diseases by the physicians or radiologists in human body. Medical images are used to observe any abnormality in different parts of human body which include Magnetic Resonance Imaging (MRI), Computed Tomography(CT) scan, x-ray images, Ultra Sound(US) images[1,3] etc. Noise is undesired information that contaminates the quality of image. In this paper two noises are considered which are different in nature from each other viz. AWGN and speckle noise [1,4,5 , 6]. AWGN is additive while speckle noise is a multiplicative type of noise signal.
An additive noise observes the rule:
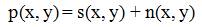
and multiplicative noise has:
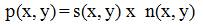
where s(x, y) is the original signal, n(x, y) denotes the noise introduced into the signal to produce the corrupted image p(x, y), and (x, y) represents the pixel location.
Gaussian noise is distributed over the signal that means each pixel in the noisy image is the sum of the true pixel value and a random Gaussian distributed noise value. It has a bell shaped probability distribution function. Speckle noise [1,4,5,6] is a multiplicative noise. This type of noise occurs in almost all coherent imaging systems such as laser, acoustics and synthetic aperture radar (SAR) imagery. Speckle noise is a multiplicative noise hence it is required to convert a noisy image to its distribution.
Wavelet transform based filtering denoises the images in terms of improvement in picture signal to noise ratio (PSNR) [2,3,8,9]. AWGN and speckle noises are different in nature but the performance of the DTCWT [1,10,11] based filter is better to remove both types of noises efficiently. Different types of thresholding [9,11,12,13,14] techniques are available but bivariate shrinkage function outperforms all of them.
Kongo et al. (2012) implemented Dual-Tree Complex Wavelet Transform (DTCWT) to remove speckle from ultrasound images by combining DTCWT with bivariate- Shrink and Visu-shrink. It improves quality of image without generating any noticeable artifact and eliminates noise without affecting either edges or texture[1] . Sveinsson etal. (2002) implemented Double Density Discrete Wavelet Transform (DD-DWT) method which removes speckle noise effectively and almost it exhibits shift invariance property [4]. Wen et al. (2008) proposed 2-D hybrid transform for despeckling ultrasound images. In this method conventional 2-D Discrete Cosine Transforms (DCT) and 2- D DWT was hybridized [5]. Santosh et al. (2011) developed a method by combining DTCWT and Adaptive Median Filter (AMF). AMF is efficient in removing impulse noise and DTCWT outperforms other methods to de-speckle [6]. Dengwen et al. (2008) proposed a new thresholding method called block shrink for image denoising. It is completely data-driven. It utilizes the pertinence of the neighbor wavelet coefficients by using the block thresholding. [9].El-Shehaby et al. (2009) introduced DTCWT to overcome the disadvantages of the traditional fully decimated Discrete Wavelet Transform (DWT). DWT lacks in shift invariance and directional selectivity properties [10]. Hill et al. (2012) introduced Un Decimated Dual Tree Complex Wavelet Transform (UDTCWT) which provides phase and orientation information compared to a simple undecimated wavelet transform and phase orientation information were added [11]. Chen et al. (2004) proposed wavelet thresholding by incorporating neighboring coefficients hence it is called as neigh-shrink; its performance is better over Wiener filter and other conventional wavelet denoising approaches [13]. Zhao et al. (2009) implemented a discrete multi-wavelet transform to remote sensing image denoising. Multiwavelets provide orthogonality and symmetry properties simultaneously which makes it more suitable for image denoising [20] .
From the above literature survey, it is concluded that wavelet approach outperforms many other filtering techniques. Much research has been done and various expensive wavelet transforms have been implemented to denoise the corrupted images. Selection of thresholding is very important for denoising the images. Many thresholding functions have been implemented; in which bivariate shrinkage function outperforms.
In this paper DTCWT technique is used for denoising the medical images by applying bivariate shrinkage function.
Discrete wavelet transform can be improved to obtain an expansive wavelet transform in place of a critically sampled one. There are various kinds of expansive DWT's; DTCWT [10] is one of them. The DTCWT of a signal X is obtained by using two critically sampled DWT's in parallel on the same data, as shown in Figure 1. It outperforms the separable DWT for image denoising. The DTCWT is 4-times expansive which is oriented in six distinct directions [15] .
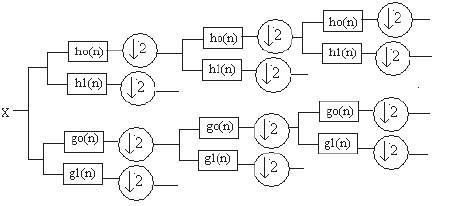
Figure 1. Dual Tree Complex Wavelet Transform
A non-Gaussian bivariate probability distribution function is discussed to model the statistics of wavelet coefficients of images. This model captures the dependence between a wavelet coefficient and its parent. It is a soft thresholding [3,9,11,14,15] approach; which is derived by using bayesian estimation theory.
This shrinkage function depends on both the coefficient and its parent; hence yields improved results for wavelet based image denoising.
Let w represent the parent of w (w is the wavelet coefficient at the same position as w , but at the next coarser scale.)
Then
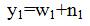
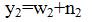
Where y1 and y2 are noisy observations of w1 and w2 and n1 and n2 are noise samples. It can be written as:
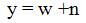
Where

The non-Gaussian bivariate probability distribution function (PDF) is given by:
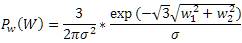
In this paper, w and w are uncorrelated, but not independent. The MAP estimator of w yields the following bivariate shrinkage function [15]
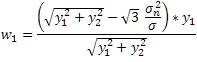
For this bivariate shrinkage function, the smaller the parent value; the greater is the shrinkage.
In this paper, image denoising technique is implemented using DTCWT by applying bivariate thresholding to remove AWGN and speckle noise signals using a single filter [16,17,18]. The following steps are applied to remove AWGN and Speckle noise [6,17,18]:
Logarithmic transform is used to convert multiplicative function into additive function. Flow diagram for denoising technique is shown in Figure 2.
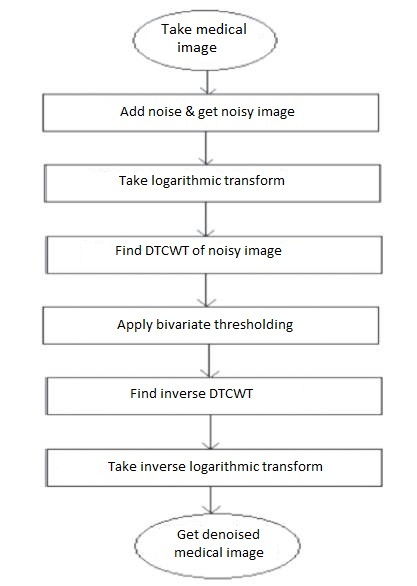
Figure 2. Flow diagram of proposed method
To measure the performance of the denoising techniques, several parameters are used. The most common parameters are PSNR [2,3,8and9] and Mean Square Error (MSE). PSNR is calculated between denoised image and original image; which is defined as [2,9 ]:

where n is the number of bits per symbol and MSE is the mean square error between the denoised and original image. MSE can be calculated by taking the difference between two images pixel by pixel, square the result and finally average the results [19].
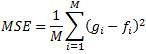
Higher value of PSNR improves the performance of the denoising method.
DTCWT based filtering is applied to the noisy medical images which are corrupted by either AWGN or speckle noise signals. In the first experiment, the medical images are corrupted by AWGN with different values of variance (σ2) and then, by using proposed method denoised images are obtained. Figure 3 shows original image and denoised imaged images after filtering which were corrupted by AWGN with variance (σ2) value ranges from 0.01 to 0.05 respectively.
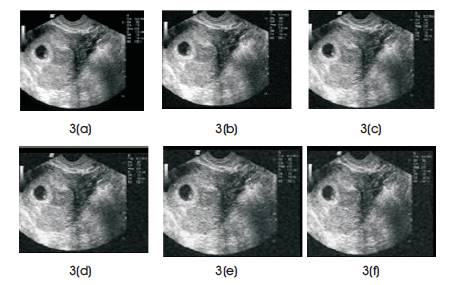
Figure 3(a) Original image (b) to (f) denoised images which are corrupted by AWGN with variance (σ2 ) from 0.01 to 0.05 respectively.
Table 1 shows the MSE and PSNR values calculated between original image and filtered image restored by DTCWT based filter applying bivariate shinkage corrupted by different values of AWGN ranges from 0.01 to 0.05 respectively.
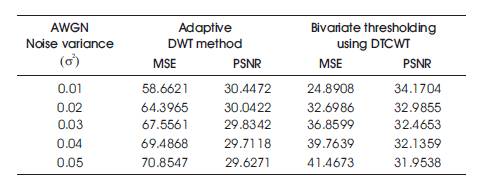
Table 1. MSE and PSNR values by different values of AWGN ranges
Figure (4) shows original image(a) and denoised imaged images after filtering which were corrupted by speckle noise with variance (σ2) ranges from 0.01 to 0.05 respectively
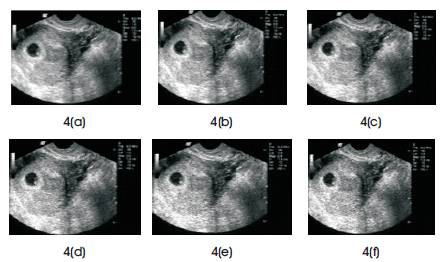
Figure 4(a) Original image (b) to (f) denoised images which are corrupted by speckle with variance (σ2 ) from 0.01 to 0.05 respectively
Table 2 shows the MSE and PSNR values calculated between original image and filtered image restored by DTCWT based filter applying bivariate shinkage corrupted by different values of speckle noise ranges from 0.01 to 0.05 respectively.

Table 2. MSE and PSNR values by different values of speckle noise ranges
From the above experiments it is clear that DTCWT with bivariate thresholding exhibits better performance than the conventional adaptive DWT methods. It removes AWGN as well as speckle noise from the medical images efficiently and provides high PSNR values; though both the noise are different in characteristics.