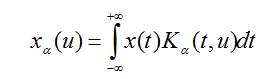
Rapid growth of high quality multimedia (HD) and exchange of data over internet with less storage space and fast processing attracted researchers in the area of compression. Compression is the technique of reducing the image size without degrading the quality of the image. In this work, a commuting matrix with random discrete Fourier transform (DFT) eigenvectors is first constructed. A Random Discrete Fractional Fourier Transform (RDFRFT) kernel matrix with random DFT eigenvectors and eigenvalues is then utilized in image compression. The RDFRFT has an important feature that the magnitude and phase of its transform output are both random. Later, a compression scheme based on random discrete fractional Fourier transform is compared with Discrete Cosine Transform (DCT) and discrete wavelet transform (DWT) based image compression schemes. The given image is subdivided and RDFRFT is applied for each subdivided image to transformed coefficients and reverse order of RDFRFT is applied for reconstruction of original images. The performance of compression scheme based on RDFRFT shows better performance over DFRFT, DCT and DWT based scheme for any multimedia contents. The performance of the proposed scheme is observed on JPEG standard image for prime evaluation parameters such as Peak Signal-to-Noise Ratio (PSNR), Mean Square Error (MSE) and Compression Ratio (CR) for RDFRFT, DCT and DWT based scheme on MATLAB software platform. In addition, the proposed scheme has following advantages: it shows the same computation complexity as DFRFT based system and the feature of additional security can also be incorporated with RDFRFT which is not very significant in case of FRFT and DFRFT based system.
Information is generated in various forms such as text, audio, image, video, etc., which are commonly referred to as multimedia content. Within a very short period, availability of inexpensive yet powerful digital cameras and video recorders in the consumer world has further accelerated the pace of research and development in the area of compression. In image processing, uncompressed images occupy a large amount of memory in RAM and in storage media, and they can take more time to transfer from one place i.e. source to destination. Ultimately compression intended to yield a compact representation of raw data, by reducing the storage/transmission requirements. Compression is achieved by the removal of three major types of redundancies: coding redundancy, inter-pixel redundancy, psycho-visual redundancy [1]. The compression techniques are broadly classified into two categories Lossless compression technique and Lossy compression technique [2]. In lossless compression techniques, the original image can be perfectly recovered from the compressed (encoded) image. Lossless compression is used only for a few applications with stringent requirements like medical, defense and research purpose etc, at smaller Compression Ratio (CR). While lossy compression schemes provide much higher CR than lossless schemes, but the quality of the reconstructed images is not adequate for all applications, where quality of data is more valuable than size reduction.
The contemporary digital image compression techniques in transform domain use various mathematical transforms like Karhunen-Loeve transform, Discrete Walsh-Hadamard transform, Hartley transform, Discrete cosine transform, Fractional cosine transform (FRCT), Wavelet transform, Singular value decomposition transform (SVD), DFT, FRFT, DFRFT and many more for compression [3]. In view of the proliferation of digital multimedia data, it is imperative that the data be mapped from the data domain (in which there are usually redundancies) to a different one (the transform domain) for efficient and economical storage and transmission. Transforms by themselves do not provide any compression. However, by reallocation of the energy in the data, transforms provide the possibilities for compression. Techniques such as adaptive quantization and entropy coding applied to the transform coefficients can result in significant reduction in bit rates. Depending on the quality levels required by the end user, other parameters such as human visual/acoustic sensitivity, adaptive scanning, statistical modeling, and variable length coding would further contribute to the bit rate reduction. Generally transforms, wavelet transforms in particular, are well suited for scalable coding (in spatial or temporal domains). This concept facilitates data transmission in embedded bit-stream format, providing for multi-resolution and multi-quality (SNR) end products, subject to bandwidth limitation, processing power, and cost constraints. Here the proposed scheme shows better results over DCT and DWT based compression scheme on quality basis parameter. The compression performance is closely related to the per formance by these mathematical transforms in terms of energy compaction and spatial frequency isolation by exploiting inter-pixel redundancies present in the image data. Transform coding constitutes an integral component of contemporary image/video processing applications. Transform coding relies on the premise that pixels in an image exhibit a certain level of correlation with their neighboring pixels. Similarly in a video transmission system, adjacent pixels in consecutive frames show very high correlation. Consequently, these correlations can be exploited to predict the value of a pixel from its respective neighbors. A transformation is, therefore, defined to map spatial (correlated) data into transformed (uncorrelated) coefficients.
The continuous fractional Fourier transform (FRFT) [4, 5] is the generalization of Fourier transform. The FRFT corresponds to a representation of the signal on an orthonormal basis formed by chirps, which are essentially shifted versions of one another in time-frequency plane by gradually changing its order from 0 to 1. It finds application in signal compression [6, 7] due to high correlation among the coefficients and compact signal representation in FRFT domain.
The DFRFT is approximate samples of the continuous fractional Fourier transform (FRT) or can be considered as a generalization of the DFT with additional degree free order parameters [6]–[8]. In [6], Pei and Yeh defined a DFRFT with one fractional order parameter by taking fractional eigenvalue powers of an eigen decomposition of the DFT matrix. The DFT eigenvectors used in [6] are Hermite-Gaussian-like and are computed from a DFTcommuting matrix given by Dickinson and Steiglitz in 1982 [9]. In [8], Pei and Hsue extend the work in [6] by taking different fractional powers for different eigenvalues of the DFT and define a new multiple-parameter DFRFT (MPDFRFT) with fractional order parameters. Later, the DFT was randomized to define the discrete random Fourier transform (DRFT) in [10] by taking random powers for eigenvalues of the DFT matrix. However, the eigenvectors of the DRFT are not random because they are Hermite- Gaussian-like and are computed using the same method proposed in [6]. Consequently, here the output phase of the DRFT is random, its output magnitude in not random as shown in [10].
In this paper, section 1 discusses on FRFT, DFRFT and RDFRFT is consolidated with their fundamental mathematical definition and on their implementation aspects. In section 2, the proposed model for image compression based on Random Discrete Fractional Fourier Transform (RDFRFT) is shown along with its block diagram and methodology of the implementation is discussed. In section 3, the major compression performance evaluation parameters are discussed i.e. PSNR, MSE and CR. In section 4, the simulation results of proposed model and their comparison with existing schemes are measured and discussed. In the last section, the article is concluded with its future research scope.
The one dimensional FRFT is defined as FRFT of order α of x(u) denoted by Xα(u) [5],
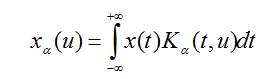
The kernel is given by,
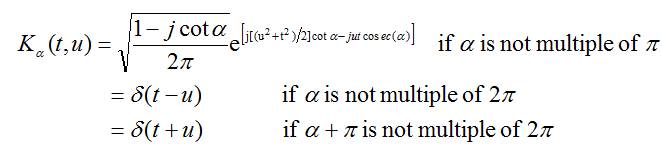
Where α=aπ/2 indicates the rotation angle of transformed signal.
Similarly, 2D FRFT can be given by,
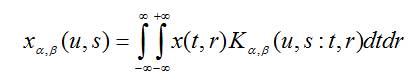
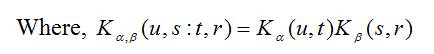
In case of two dimensional FRFT, the angle of rotations are α =aπ/2 and β =bπ/2. The signal is recovered back by 2D FRFT operation with inverted angles (-α, -β).
By using eigen vector decomposition, the N-point DFRFT is given by the following relationship [6], [11]
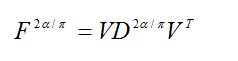
Where a=2α/π is the DFRFT order of the parameter and α indicates the rotation angle of DFRFT.
 for N is odd,
for N is odd, for N is even, and Vk is the k-th order DFT hermite eigen vector.
for N is even, and Vk is the k-th order DFT hermite eigen vector.
D2α/π is a diagonal matrix with eigen values of DFRFT in the diagonal entries. The methods for finding the DFT Hermite eigenvectors Vk are presented in [6] and [11].
The N x N DFT matrix F is given by,
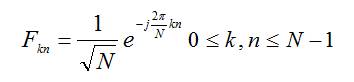
The computation for the DFRFT kernels for even and odd cases of N is done. For the odd case, equation (4) will be converted in the following form,
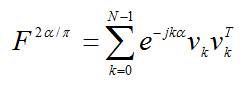
Similarly for the even value of N case, equation (4) will be converted in the form mentioned below,
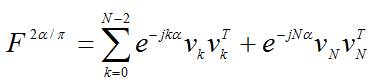
The final DFRFT output is computed as a,
For the odd values of N
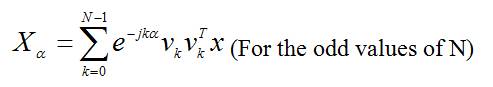
For the even values of N
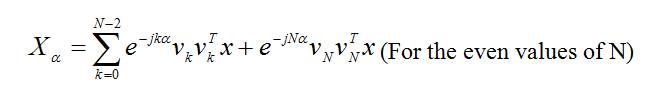
The DFRFT is further generalized on the basis of taking different fractional power for the eigen values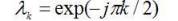 of the DFT matrix. Subsequently the N point N x N MPDFRFT matrix is given as,
of the DFT matrix. Subsequently the N point N x N MPDFRFT matrix is given as,
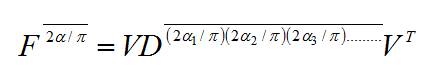
The DFT commutating matrix with orthonormal random DFT eigenvectors can be generated by taking an N x N matrix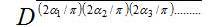 is symmetric if
is symmetric if 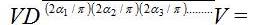 =
=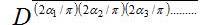 Where V is circular reversal Matrix is given by, [12]
Where V is circular reversal Matrix is given by, [12]
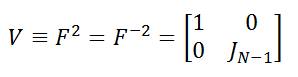
Here JN-1 is the (N-1) X (N-1) reversal matrix whose only nonzero entries are ones on the antidiagonal.
A symmetric N x N DFT commutating matrix with a random generating matrix can be derived as following:
1. Form an N x N real random matrix D whose entries are independent and uniformly distributed in the range of -1 to 1.
2. Take the V symmetric part of P of the random matrix D i.e.
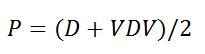
3. Take the symmetric part of P to form the random generating matrix G
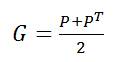
Here T denotes the transpose of the matrix.
4. The new constructed random DFT matrix is given by
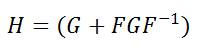
The DFT eigenvectors are either even or odd vectors. Here the two 64 x 1 random DFT eigenvectors are computed from eigenvectors of the proposed 64 x 64 random DFTcommuting matrix. The computed DFT eigenvectors are random except that they are even or odd.
With the random DFT-commutating matrix H in equation (14) and multiple parameters in equation (10), the random DFRFT with the1 x N parameter vector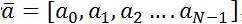 can be given by,
can be given by,
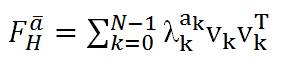
Where Vk is the orthonormal random DFT eigen vectors computed from H.
λk is the DFT eigen value corresponding to Vk and 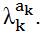 The RDFRFT
The RDFRFT 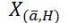 with the 1 x N random parameter vector
with the 1 x N random parameter vector 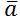 and based on H of the N x 1 input data vector x can be computed by,
and based on H of the N x 1 input data vector x can be computed by,
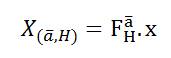
The 2D RDFRFT with parameter set 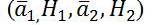 for N x M size of image Z can be given by,
for N x M size of image Z can be given by,
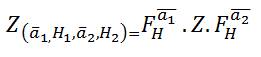
Where 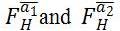 are the RDFRFT matrices
are the RDFRFT matrices
The proposed model for image compression based on RDFRFT and multiple parameter discrete fractional Fourier transform is shown in Figure 1. The model comprises four major processing blocks: sub image converter, transform, quantizer and encoder at the transmission side for providing compression where the tradeoff between the quality of reconstructed image and compression ratio for reducing the size of image is maintained.
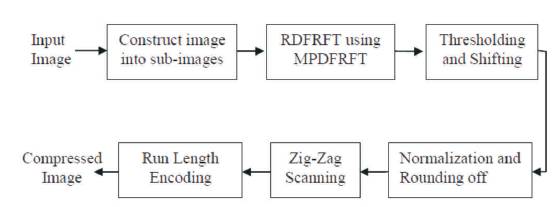
Figure 1. Image compression model based on RDFRFT
These major steps in the proposed transform coding compression model are shown in Figure 1. First, the input data (frame) are divided into blocks (sub-images). Each block is then linearly transformed. The transformed version is then truncated, quantized, and encoded. The quantization process is processed in three segments thresholding, shifting and then normalization with rounding off. Received coefficients are arranged by using zig-zag scanning and then run length encoding scheme is applied for minimizing the redundancies available in processed image. The output of the encoder is a bit stream. The following steps are followed during compression process:
Step 1: An image is converted into non-overlapped 8×8 sub images because of adopted by the international still image coding standard due to having maximum correlation for JPEG 2000 standard.
Step 2: A 2-D RDFRFT with multiple parameters is applied to each block at optimum value of fractional orders with selected suitable compression percentage as selected for different CR’s.
Step 3: The quantization of these coefficients is done to selectively eliminate or more coarsely quantize the coefficients that carry the least information. A trade off is made between image quality and compression percentage by adjusting the quantizer cutoff value.
Step 4: The optimized quantized coefficients are arranged from lower-frequency to higher-frequency components compressed by using Run length coding (RLC).
Figure 2 shows the block diagram representation of major blocks applied at the receiver side during decompression process. The bit stream is decoded and then inversely transformed to form reconstructed blocks. All the reconstructed blocks collectively produce a replica of the input image.
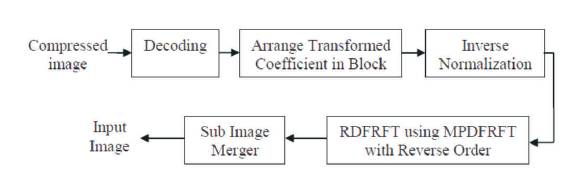
Figure 2. Image Decompression model based on RDFRFT MPDFRFT
Image compression using transform coding yields higher compression ratio, with controllable degradation of image quality. The compromise can be made between image quality and compression ratio by the suitable selection of CR or quality as well. The performance of the system is evaluated using important parameters like Peak Signal to Noise Ratio (PSNR), Mean Square Error (MSE) and compression ratio (CR).
The Peak Signal-to-Noise Ratio (PSNR) value used to measure the difference between a decoded image Z'(i, j) and its original image Z(I, j) is defined as follows. In general, the larger PSNR value, the better will be decoded image quality. And it is measured in terms of the MSE.
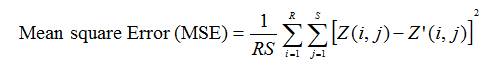
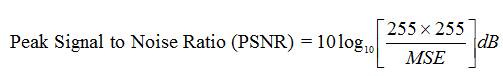
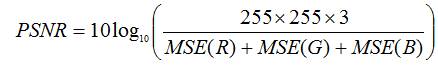
Where R and S indicate the size of the image.
It is defined as the ratio of size compressed image to the size of original image and is given below,
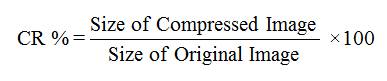
In this segment, the numerical simulations for the proposed compression scheme are shown. The simulation is done for both gray and color pepper images of sizes 512×512. Figure 3(a) shows the original pepper image and subsequently at the different compression ratios the images is generated and their respective MSE and PSNR is calculated. The order parameters varied from 0 to 1 and the optimum value for maximum PSNR and min MSE was observed. Here the fractional orders value of Figure 3 (a) input image of pepper is shown and the image is processed using the proposed compression scheme and obtained results for CR at 25, 50, 75 and 80 percent in Figure 3 (b), (c), (d) and (e) and shows decompressed images respectively. The result shows that the quality for 50% CR is significant, while it degrades as these is increase in 75% CR and as CR progress higher, the PSNR decreases rapidly and quality of image degrades.
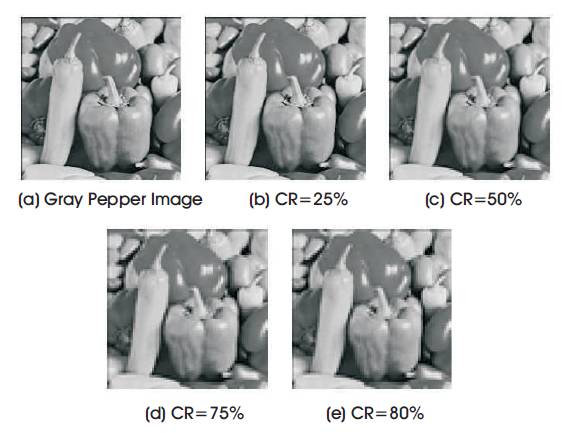
Figure 3. Decompressed images of gray pepper
In figure 4 (a) pepper color image is taken as input image while the image is processed using the proposed compression scheme and produced results for CR at 25, 50, 75 and 80 percent in Figure 4 (b), (c), (d) and (e) which show the decompressed images respectively. The measured result depicts that the proposed scheme shows better results for color images than gray scale image when higher CR is selected particularly when CR is considered from 50% to 80%. For higher CR also the proposed scheme offers higher PSNR and minimum MSE.

Figure 4. Decompressed images of colour pepper
In Figure 5 (a), baboon color test image is taken as input image. The image is processed using the proposed compression scheme and produced results for CR at 25, 50, 75 and 80 percent in Figure 5 (b), (c), (d) and (e) which show the decompressed images respectively. The measured result depicts that the proposed scheme shows better results for color images than gray scale image when higher CR is selected, particularly when CR is considered from 50% to 80%. Hence the results are obtained for color pepper image. The image quality is fairly good even at a very high value of 80 percent CR.
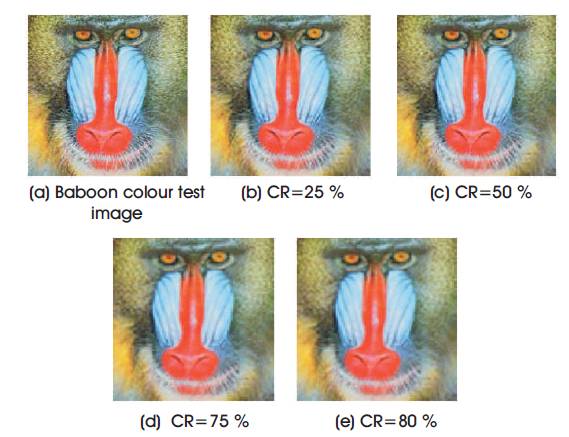
Figure 5. Decompressed images of Baboon colour
Figure 6 depicts the variation of pepper color and gray image with the proposed compression scheme along with the existing DCT and DWT based compression scheme given by Prabhakar in [13]. The graph is plotted for CR in the range of 25 to 80 percent and respective PSNR is calculated for the proposed scheme and compression scheme based on DWT and DCT.
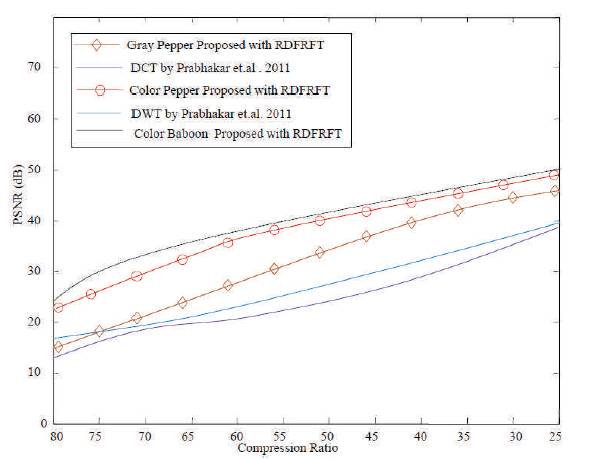
Figure 6. Variation of PSNR versus CR
It can be seen from the graph that the proposed compression scheme offers high value of PSNR at every value of CR in the range of 25 to 80 percent compared to the respective values of PSNR obtained from DCT and DWT based compression schemes. Also for color images, even at high values of CR, there is not much degradation in image quality.
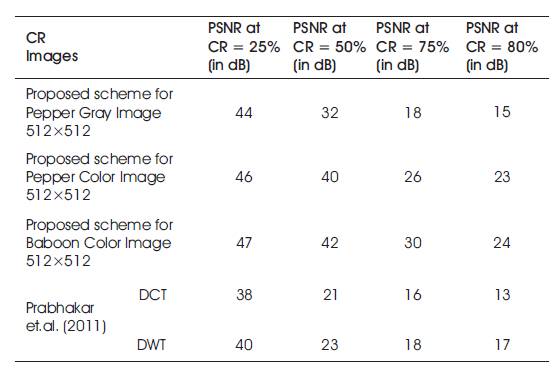
Table 1. Performance Comparison of compression scheme with DCT, DWT and RDFRFT
Image compression using RDFRFT was proposed and implemented successfully. The eigenvectors of RDFRFT kernel matrix are random DFT eigenvectors as they are computed from eigenvectors of a random DFT commuting matrix and eigenvalues of a RDFRFT are taken as random powers of DFT eigenvalues. Hence the magnitude and phase of the transform output of the RDFRFT are random. The proposed compression model using RDFRFT shows better performance at different compression ratios. The PSNR of proposed scheme is 9dB and 7dB better than DCT and DWT based scheme at 25% CR. The proposed scheme also shows better PSNR 11dB and 7dB at higher 80 % CR over DCT and DWT based scheme for baboon colour image. Table 1 shows the Performance Comparison of compression scheme with DCT, DWT and RDFRFT. Therefore image compression using RDFRFT can prove to be very useful in image compression in transform domain. As a future scope, same compression scheme is combined with encryption scheme to utilize the advantage of bandwidth and security as an encryption.