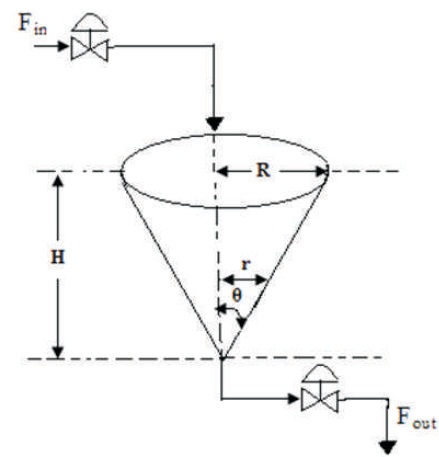
Figure 1. Geometrical Cross-sectional View of the Conical Tank Process
Recently, the PID Controllers are widely used in industries for nearly a century due to its features, such as simplicity, flexibility, and efficiency. Recently, the control concepts of non-linear processes in the industries are turned towards the attention of the intelligent controllers, such as Genetic Algorithm tuned PI Controllers, Neural Networks tuned PI Controller, Model Predictive Controller, Nonlinear Adaptive Controller, Fuzzy Logic based Controller, Neuro tuned Predictive Controller, etc. This paper focuses on the Investigation of Genetic Algorithm tuned PI Controller for the Nonlinear Conical tank Level Process. The Conical tank is a highly nonlinear process in which the variation in the area of cross section of the process tank level system with change in shape. In the above work, the Genetic Algorithm tuned PI Controller is especially designed for the control of nonlinear conical tank level process for the exact level maintenance. Also, the designed Genetic Algorithm tuned PI Controller is compared with Conventional PI Controller in Servo operation and Regulatory operation.
In the chemical process industries, many more challenging control problems arise, due to the nonlinear dynamic behaviour of the system, Constraints on the manipulated and controlled variables, Uncertain time var ying parameters, Interaction between the manipulated and controlled variables, Delay input or dead time measurement as well as the unmeasured frequency disturbances. The Proportional Integral Derivative (PID) Controllers are widely used in process industries due to its features, such as simplicity, flexibility, and efficiency. A fine tuning concept for the closed loop system was developed (Ziegler & Nichols, 1942). The standard methods for tuning of controller includes such as, Zeigler and Nichol’s (1942), Ultimate Cycling Method Open loop tuning method (Coon, Cohen, & Coon, 1952) and the future of PID tuning (Åström & Hägglund, 2001).
The performance and comparison between PID and Dead time compensating controller concept was introduced by Ingimundarson and Hägglund (2002). The tuning concept for the fuzzy logic controller for the nonlinear conical tank process was developed (Madhubala, Boopathy, Chandra, & Radhakrishnan, 2004). Similarly, the Wiener Model PI Controller Real time Implementation of the conical tank concept was developed (Bhaba, Sathishbabu, Asokan, & Karunanithi 2007). Valarmathi, Devaraj, and Radhakrishnan (2007) introduced the adaptive enhanced genetic algorithm base proportional integral controller tuning for the pH process. The neuro based model reference adaptive control of a conical tank concept was developed (Bhuvaneswari, Uma, & Rangaswamy, 2008). Again, the design of Intelligent Controller for non-linear conical tank process was developed (Nithya et al., 2008).
A new CDM-PI control scheme for a conical tank liquid level maintenance real time implementation concept was developed (Bhaba & Somasundaram, 2009). Manic, Sivakumar, Nerthiga, Akila and Balu (2009) have introduced the concept of design of the Plant estimator model using Neural Network for Conical tank process. In this work, the Genetic Algorithm tuned PI Controller is compared with Conventional PI Controller through Servo and Regulatory operations.
The schematic diagram of the nonlinear conical level tank process is shown in Figure 1. The conical tank level process consists of an inflow rate, outflow rate, and the change in height, with respect to time.

Figure 1. Geometrical Cross-sectional View of the Conical Tank Process
The mass balance equation governing the system dynamics (Levine, 2000) are given by Equations (1) and (2).
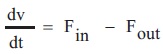
where,
Fin = Inlet flow rate of the conical tank (cm3/s)
Fout = Outlet flow rate of the conical tank (cm3/s)
R = Top radius of the conical tank (cm)
H =Total height of the conical tank (cm)
h = Height of the water in the conical tank (cm)
r = Radius of the water in the conical tank (cm)
On applying the trigonometric geometry theory, the conical tank tangent angle is obtained as,
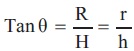
The mathematical representation of flow rate with respect to height is given by,
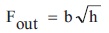
where,
b=Valve constant
The volume of the cone can be written by the mathematical formulae
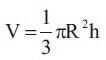
From equations (1), (2), (3) and equation (4), the modified mass balance equation can be written as,
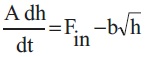
To convert a highly nonlinear conical tank process into linear approximation model by applying Taylor series, we get,
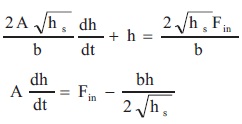
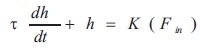
The transfer function relating the height 'h' and the inlet flow rate (Fin) with the parameters (K is the process gain, τ is the time constant of the conical tank process) can be obtained.
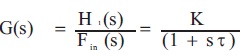
where,
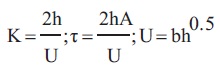
For the First Order Process with Delay Time (Liptak, 1995), the standard model is given by,
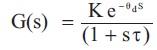
where,
K =Process gain
θd =Transport lag or delay of the process
τ =Time Constant
In the above work, the proposed method by Skogestad's tuning rule (Skogestad, 2003) for the PI Controller is given by,
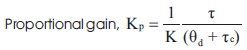

For the conical tank process, the selected transfer function model.
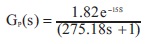
The above model is considered for the simulation studies of the conical tank process control with different control structures. Modeling parameter concept of the conical tank for the different height of obtaining the PI Controller parameters by Skogestad's tuning rule are tabulated in Table 1.
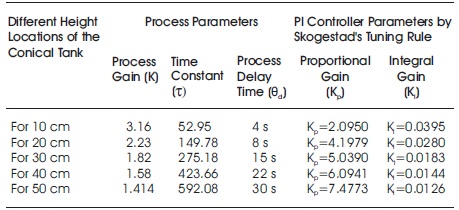
Table 1. Conical Tank Process Modeling Parameters for Different Regions and obtaining Conventional PI Controller Parameters
The Genetic Algorithm concept was first introduced by Holland (1992) and Goldberg (1989). The Genetic Algorithm (GA) is especially a random search technique, which imitates Darwin's theory of natural evolution, and the survival of the fittest approach. This technique was inspired by the mechanism of natural selection, a biological process in which stronger individuals are likely to be winners in a competitive environment (David, 1991).
The Genetic Algorithm is governed by three operations, namely selection, cross-over, and mutation.
Selection: The Selection is a stochastic method for the selection of individuals from a population, according to their fitness, to produce successive generations, and plays an important role in the Genetic Algorithm. An individual with the highest fitness has more chance to be selected for the next generation. For this work, the tournament selection method is used.
Cross-Over Operation: If the selection or reproduction is over, it is again applied for the crossover operation. In the crossover operation, the information is exchanged among the strings for the mating pool, due to which a new string is formed. Similarly, the crossover operation is mainly responsible for the global search property of the Genetic Algorithm. Crossover basically combines the substructures of two parent chromosomes to produce new features, with a specified probability.
Mutation: The final genetic algorithm operation is mutation, even though the mutation operation is scarcely used, it is valuable in preventing the involuntary loss of good genetic material. Mutation involves the alternation of information at a random selected bit position. The value of the chromosome at this position is changed (1 or 0 or vice versa). Normally, the mutation rate is selected with a very low value, and may be 0.075 for this work. The block diagram representation of the conical tank process, controlled by the Genetic Algorithm tuned PI Controller is shown in Figure 2. The main parts are: the conical tank level process and the Genetic Algorithm to find the PI parameters such as proportional gain (Kp) and integral gain (Ki). The process output is a controlled variable, which is again applied as an input to the set point value. The value of error is obtained as the difference between the set point value and measured value.

Figure 2. Block Diagram Representation of the Genetic Algorithm Tuned PI Controller for the Conical Tank Process
The flowchart representation of the Genetic Algorithm tuned PI Controller for the conical tank process is shown in Figure 3. The Genetic Algorithm tuned PI Controller, consists of the following steps:
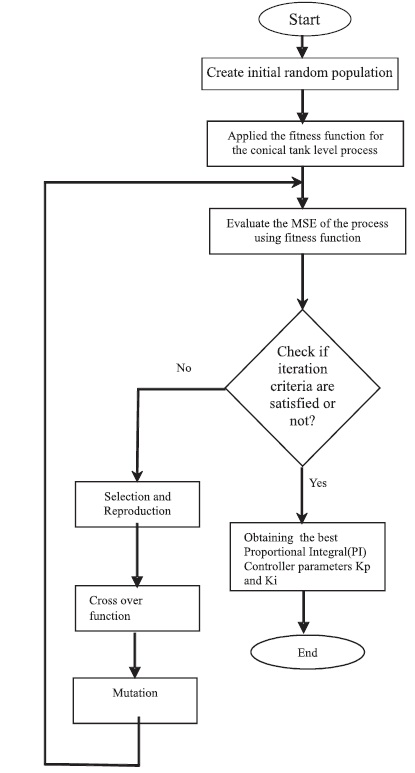
Figure 3. Flowchart of the Genetic Algorithm Tuned PI Controller for the Conical Tank Process
Step 1: Initial setting of the Genetic Algorithm (GA) parameters, and generating an initial random population interval.
Step 2: Evaluate the fitness function for each chromosome.
Step 3: Check whether if the iteration criterion is satisfied or not.
Step 4: If satisfied, generate the PI Controller parameters such as Proportional gain (Kp) and Integral gain (Ki).
Step 5: If not satisfied, apply the genetic operations, such as selection, crossover, and mutation.
The graphical representation of the Fitness function with Generation and the Evaluation of Kp and Ki versus Generation are shown in Figures 4 and 5.
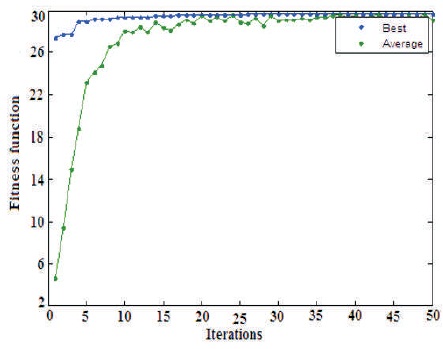
Figure 4. Graphical Representation of the Fitness Function with Generation
In Servo operation, the process or load variable needs to be a constant and the set point value is a variable. For the variation of the set point value, the closed loop servo response for the nonlinear conical tank process is obtained, using the Genetic Algorithm tuned PI Controller values such as Proportional gain (Kp) and Integral gain (Ki). The simulation diagram of the Genetic Algorithm tuned PI controller for the height of 20 cm from 0 to 500 seconds and the height is increased 10 cm from 500 to 1000 seconds as shown in Figure 6.
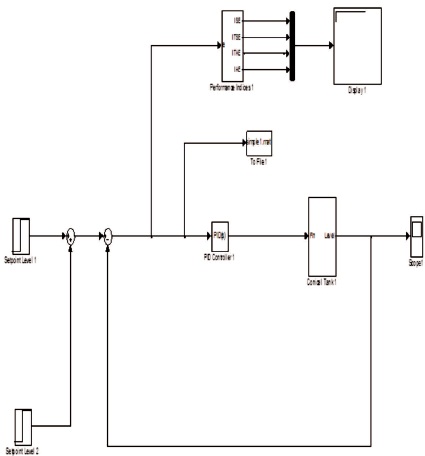
Figure 6. Simulation Diagram of the Genetic Algorithm Tuned PI Controller for the Conical Tank Process in Servo Operation
In Regulatory operation, the process with the load variable is varied and the set point value is kept constant. With the variation of the load value, the closed loop response for the nonlinear conical tank process is obtained using the Genetic Algorithm tuned PI Controller values such as proportional gain (Kp) and integral gain (Ki). The simulation diagram of Genetic Algorithm tuned PI Controller with the height of 30 cm from 0 to 1000 seconds and with +10% load changes after 800 seconds through step signal is shown in Figure 7.
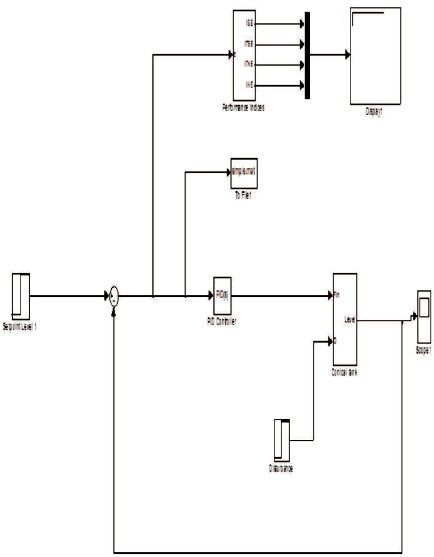
Figure 7. Simulation Diagram of Regulatory Operation with the Genetic Algorithm tuned PI Controller for the Conical Tank Process in Servo Operation
Table 2 shows the comparison of Genetic Algorithm tuned PI Controller and the Conventional PI Controller for the conical tank process in Servo and Regulatory operations.
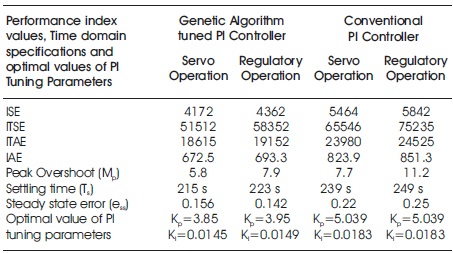
Table 2. Genetic Algorithm Tuned PI Controller Compared with the Conventional PI Controller for Conical Tank Process in Servo and Regulatory Operations
In this research work, the paper proposes the modelling of genetic algorithm tuned PI controller for the nonlinear conical tank level process and compares the performance with conventional Proportional Integral (PI) controller. The Matlab simulation results are obtained for the above mentioned controllers, such as genetic algorithm tuned PI controller with conventional PI controller by adjusting set point and load changes through servo and regulatory operations. From the above simulation results, it is observed that the performance of genetic algorithm tuned PI controller produces better response compared to the conventional PI controller for the non-linear conical tank process.
The authors are grateful for the valuable comments and suggestions of the reviewers, which has enhanced the strength and significance of the research work.