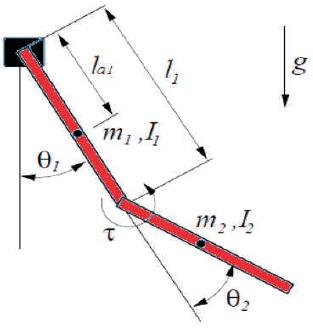
Figure 1. 2-Link Robot Manipulator
Robot manipulators are multi-link nonlinear system with higher uncertainties and disturbances. To obtain desired accuracy and high performance, the controlling of robot should be in real time. Due to higher uncertainties and disturbances like variation in pay load frictions, the performance and accuracy of the system is highly deviated from desired performance and accuracy. This paper presents PD Fuzzy logic controller based scheme to track the desired trajectory of 2-link robot manipulator. In this PD fuzzy logic controller based scheme, the output of the system is fed to Fuzzy logic controller as input. The error and change in error is given as input to Fuzzy logic controller and this control scheme is capable in compensation of disturbances. In MATLAB environment, the simulation is performed and the reference trajectory of robotic system is tracked with minimum error.
In this proposed paper, to obtain adaptive tracking control of 2-link robot manipulator and to track the desired or reference trajectory of 2-link robot manipulator, the Proportional Derivative (PD) controller is used with fuzzy logic controller. This provides the control input to each link of 2-link robot manipulator. Here, the input of fuzzy logic controller is error signal, which is the difference between actual and desired angular position. According to error signal, each fuzzy logic controller compensates the disturbances in robotic system and obtains desired angular positions. The mathematical modeling of 2-link robot manipulator is performed using Euler-Lagrange equation with the help of potential and kinematics energy of both links of robot manipulator (Sumathi, 2005).
Robots are introduced in industries for increasing productivity, quality improvement, and for replacement of human in hazardous task. Mostly, robot manipulators are driven by actuators which may be electrical, hydraulic, or pneumatic. Robot manipulator dynamics describe how the robot moves in response to these actuators (Edwards, 1984). Robot manipulators are multilink nonlinear system with higher uncertainties and disturbances (Rastogi & Prasad, 2015).
Robots having nonlinear and uncertain behavior have strategies which are basically used for controlling the robot that are conventional, robust, adaptive, and optimal control (Khan, ul Islam, & Iqbal, 2012). The conventional control strategies such as PD, PID and PI are mostly used in various process controls because of easy implementation of these controllers, but they are less capable in process control to obtain desired level of per formance when unstructured or structured uncertainties and disturbances are involved in the system (Kelly, 1997). In case of conventional controllers, the exact dynamics of system should be known. To remove these problems when dynamics of system is unknown and mathematical formulation is difficult then fuzzy based control scheme can be used with conventional controllers (Mohammed, Bendary, & Elserafi, 2016).
Most of the manipulators are driven by electric, hydraulic, or pneumatic actuators, which apply torques or forces at the joint of the robot (Jimenez & Al Hadithi, 2009). Using a set of nonlinear second order ordinary differential equation, the dynamics of robot manipulators is described, which depends on the kinematic and inertial properties of the robot. With the help of Euler Lagrange equation using potential and kinetic energy of both links, the 2-link robot manipulator dynamics is derived.
Intelligent control techniques such as Fuzzy Logic Control (FLC) that consists of knowledge based system is useful for compensation of disturbances. Fuzzy logic incorporates human thinking in control application (Lochan & Roy, 2015). Fuzzy control technique is used to handle linear and nonlinear system to control complex multivariable system and for decision making (Chien, 1990).
2.1 2-Link Robot Manipulator
The dynamic equation of 2-link robot manipulator can be obtained by Euler-Lagrange method. Considering a robot arm where the link mass is concentrated at la1 distance for link-1 and at la2 distance from link-2 is shown in Figure 1. The joint variable vectors are q = [θ1 θ2]T and torque vector is = [M1 M2]T, as shown in Figure,θ1 is position from joint-1 and θ2 is position from joint-2. The moment of inertia I1 and I2 are considered about the pivots.

Figure 1. 2-Link Robot Manipulator
The kinematics are given by (Ouyang & Zhang, 2004),
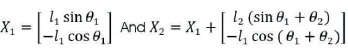
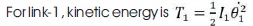
And for link-2 kinetic energy is,
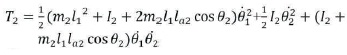
Now potential energy for link-1 and link-2 is,
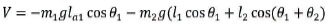
Lagrangian for entire arm is,
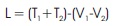
Thus, we can write Lagrangian equation in the form of
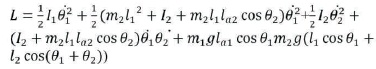
According to Euler-Lagrange,
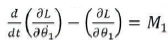
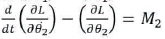
Thus torque equation can be written as:
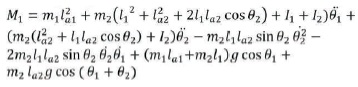
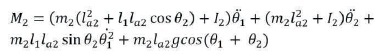
The equation M1 and M2 can be arranged in matrix vector form as follows:
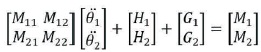
where
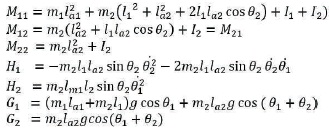
The dynamic equation of robot can be written as (Chien, 1990),
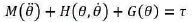
where θ1 and θ2 are joint variables and M(θ) is inertia matrix, H(θ, θ) is coriolis and centrifugal vector and G(θ) is gravity vector of the manipulator.
The related properties are (Edwards, 1984),
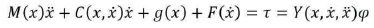
where φ is unknown parameter matrix and Y(x, x, x) is a known parameter called regressor.
Skew symmetric matrix property:
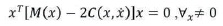
The PID controller continually calculates the error which is the difference between desired set point and actual measured variable and based on proportional (P), Integral (I), and Derivative (D) terms, it applies the correction (Spong, Hutchinson, & Vidyasagar, 2012). All these quantities are multiplied by each tuning constant and added together to produce the current controller output u (t) (Su, Sun, & Duan, 2005).
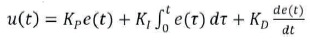
Here KP is proportional gain constant, Kl is integral gain constant, and KD is derivative tuning constant. The e(t) is error which is the difference between set point r(t) and process variable c(t) in time t. If error is large or rapid changing, then this controller makes large correction by generating the large output. The PD controller can be obtained from equation (13) by making the integral gain constant Kl =0. Then the output of PD controller can be given as,
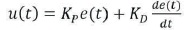
and the transfer function is
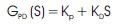
The PD control process in the proportional mode produces the control output or control action, which is directly proportional of error, and in the derivative mode, controller produces control action which is proportional to the change in error (Ouyang & Zhang, 2008). At each moment of time, the value of the control variable is given by the current value of the error and the derivative of error signal, with the constants KP and KD both are weighted, respectively.
To mathematical models, the Fuzzy logic transfers expert knowledge and to estimate dynamics of system Fuzzy system uses fuzzy logic. To control system, Fuzzy controllers use fuzzy if-then rules (Botsali, Tinkir, Kalyoncu, & Önen, 2010). Fuzzy control provides a formal strategy to manipulate, represent and implement human heuristic knowledge about how to control system, when mathematical formulation of dynamics is much complex then with the help of FLC without exact model system can be controlled and it have good function approximation capability (Prabhu & Garg, 1998). FLC system is as shown in Figure 2.
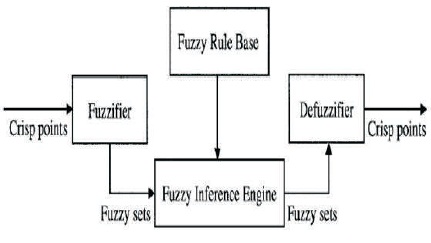
Figure 2. Basic Configuration of Fuzzy System
The four main components of Fuzzy logic controller are (Purwar, Kar, & Jha, 2005):
The Fuzzy Logic Control (FLC) uses the IF-THEN Rules. The Fuzzy rule base consists of collection of IF-THEN Rules.
In this paper, centered defuzzification and seven level triangular membership functions are used for error and change in error inputs. Thus, total 49 rule base are present. Here in this paper, the error and change in error is given as input to the fuzzy logic controller through PD controller. The two separate PD-Fuzzy controllers are provided at each joint of robot manipulator.
The IF-THEN Rules for fuzzy logic system can be given as,
R(yj): If x1 is Al1 and x2 and Al2 and …. and x2 is Alm.
Then yj is Blj and where x=[x1 x2… xm]T is input vector to fuzzy logic system. Ali and Blj are linguistic variables of fuzzy sets in subspace Ui and Vj described by their membership functions μlAi(x) and μlBi(yj), where i=1, 2, … m and j=1, 2,… n and l=1, 2, … M.
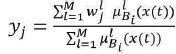
where x(t) is error and change in error and wlj center of area of membership functions.
To track the desired or reference trajectory of 2-link robot manipulator, the Proportional Derivative (PD) controller is used with fuzzy logic controller as shown in Figure 3, which are provided to the control input to each link of robot manipulator. Here the input of fuzzy logic controller is error and change in error. According to these error signals, each fuzzy logic controller compensates the disturbances in robotic system and obtains desired position.
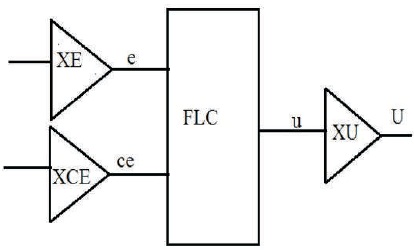
Figure 3. Block Diagram of PD Fuzzy Controller
The simulation of PD fuzzy controlled 2-link robot manipulator is performed in MATLAB environment to obtain the desired tracking control. The 2-link robot manipulator is modeled in sim-mechanics. Simulink model of PD Fuzzy controlled 2-Link robot manipulator is shown in Figure 4.
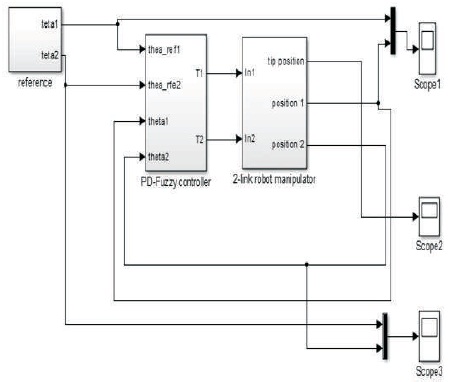
Figure 4. Simulink Model of PD Fuzzy Controlled 2-Link Robot Manipulator
The robot manipulator parameters which are used in simulation are given in Table 1 as below:

Table 1. Parameters of 2-Link Robot
The membership functions used at input port of fuzzy logic controller as error and as change in error are shown in Figures 5 and 6, respectively and membership function for output are shown in Figure 7 and the 49 rule base is used.
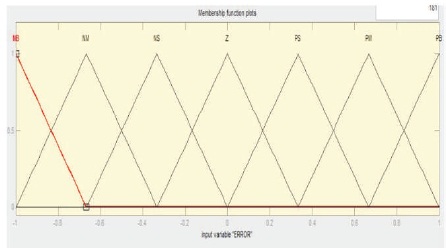
Figure 5. Membership Function for First Input as Error
Figure 6. Membership Function for Second Input as Change in Error
Figure 7. Membership Function for Output
Where in rule base Table 2, E is error, CE is change in error and NB is negative big, NM is negative medium, NS is negative small, Z is zero PB is positive big, PM is positive medium, and PS is positive small.

Table 2. Rule Base
To obtain the performance of fuzzy PD controller, various simulations are performed on 2-link robot manipulator by using MATLAB. For simplicity, all the masses are concentrated on center as a point mass.
Robot manipulators are highly non-linear systems in which system dynamics is not known accurately. Conventional controller like PD may not work in different operating conditions, so controller should be designed in such a way that it is based on “human operator” that is fuzzy control technique.
A new hybrid control scheme that is PD-Fuzzy is used to overcome problems associated with different operating conditions. In Figures 8 and 9, joint-1 and joint-2 trajectory tracking with respect to reference signal is shown. Below trajectory tracking figure represents the good tracking characteristics and satisfactory performance of PD fuzzy controller used for 2-link manipulator. The desired reference trajectory is tracked successfully with small error.
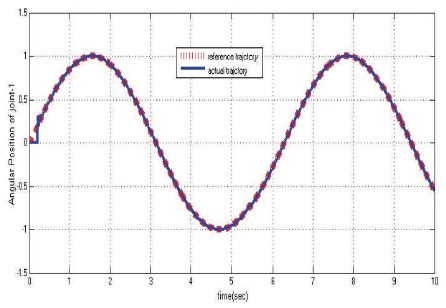
Figure 8. Joint-1 Angular Position Tracking
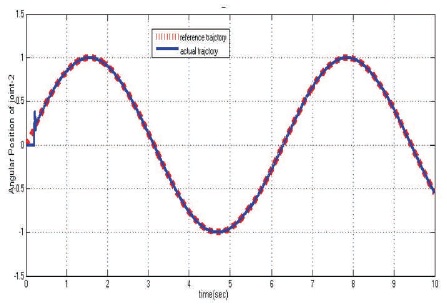
Figure 9. Joint-2 Angular Position Tracking
Figures 10 and 11 present the tracking error and the settling time of joint-1 and joint-2 as 0.05 s and 0.07 s, respectively. After settling time, error converses to zero for both the joints. This shows the satisfactory performance of PD fuzzy controller.
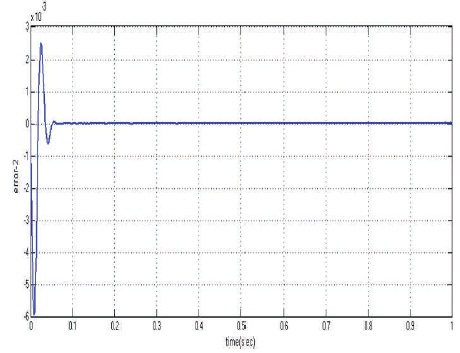
Figure 10. Error in Position Tracking of Joint-1
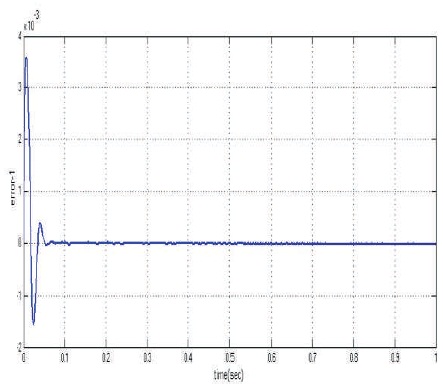
Figure 11. Error in Position Tracking of Joint-2
To obtain the adaptive tracking control, the modeling and simulation of PD-Fuzzy logic controlled 2-link robot manipulator is accomplished in a MatLab environment. The desired reference trajectory is tracked for the new hybrid control scheme PD-Fuzzy can be used to overcome problems associated with different operating conditions. Trajectory tracking of joint-1 and joint-2 with respect to reference signal with minimum tracking error is possible. The trajectory tracking represents the good tracking characteristics and satisfactory performance of PD fuzzy controller used for 2-link manipulator. The desired reference trajectory is tracked successfully with small error. The tracking error is much smaller after 0.05 s and 0.07 s for both joint-1 and joint-2, respectively, where the error converges rapidly to zero.
This work can be extended to multi-link higher order robot manipulator control. And this PD fuzzy control scheme can be extended in fuzzy Sliding Mode Control (SMC) of robot and adaptive fuzzy sliding mode control.