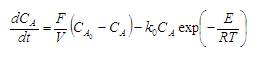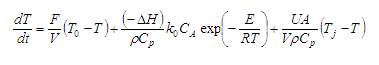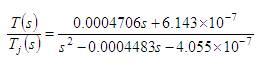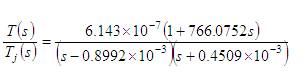Design Of PID Controllers for Unstable Second Order Plus Time Delay Systems by Equating Coefficient Method
C. Ravi Kishore * R. Padma Sree **
* Department of Chemical Engineering, AU College of Engineering (A), Visakhapatnam, India
** Professor, Department of Chemical Engineering, AU College of Engineering (A), Visakhapatnam, India.
Abstract
Design of Proportional Integral Derivative (PID) controllers for Unstable Second Order systems Plus Time Delay (USOPTD) with/without a zero using equating coefficient method is proposed in this paper. The method is based on equating the corresponding coefficients of s , s2 , s3 of the numerator of the closed loop transfer function for servo problem to α1 ,α2 , α3 times that of the denominator. The time delay term in the denominator of the closed loop transfer function is written as, 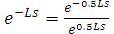 and it is expanded using Taylor series expansion upto four terms both in the numerator and denominator.This makes the numerator and denominator as polynomial of s. The time delay term in the numerator shifts the response on time axis and is not considered in the design problem. By equating the corresponding coefficients of s, s2 and s3 in the numerator with α1 , α2 , and α3 times that of the denominator; three linear equations are formulated and solved for the PID controller parameters. In the proposed work, the coefficients α1 , α2 , and α3 are obtained by minimizing Integral Time weighted Absolute Error (ITAE) for servo problem using fminunc of Matlab. Simulation results on various transfer function models and on the nonlinear model equations of jacketed CSTR (Continuous Stirred Tank Reactor) carrying out first order exothermic reaction are given to demonstrate the effectiveness of the proposed method. The smooth functioning of the controller is expressed interms of total variation. The controller performance is expressed in terms of ITAE. Nominal control performance of the proposed method is better than the existing methods.
and it is expanded using Taylor series expansion upto four terms both in the numerator and denominator.This makes the numerator and denominator as polynomial of s. The time delay term in the numerator shifts the response on time axis and is not considered in the design problem. By equating the corresponding coefficients of s, s2 and s3 in the numerator with α1 , α2 , and α3 times that of the denominator; three linear equations are formulated and solved for the PID controller parameters. In the proposed work, the coefficients α1 , α2 , and α3 are obtained by minimizing Integral Time weighted Absolute Error (ITAE) for servo problem using fminunc of Matlab. Simulation results on various transfer function models and on the nonlinear model equations of jacketed CSTR (Continuous Stirred Tank Reactor) carrying out first order exothermic reaction are given to demonstrate the effectiveness of the proposed method. The smooth functioning of the controller is expressed interms of total variation. The controller performance is expressed in terms of ITAE. Nominal control performance of the proposed method is better than the existing methods.
Keywords :
- Unstable System,
- Second Order System,
- Time Delay,
- Equating Coefficient Method,
- PID Controller.
Introduction
Open-loop unstable processes arise frequently in the Chemical Engineering practice. The open-loop Unstable First Order Plus Time Delay (UFOPTD) models and Unstable Second Order Plus Time Delay (USOPTD) models are generally used to represent such processes. The control of such processes is difficult. The difficulty increases when the process contains a time delay and a positive or a negative zero (numerator dynamics). The per formance specifications that are usually achieved for stable systems are difficult to achieve for unstable systems (Chidambaram, 1997). The closed loop performance of such processes exhibits large overshoots and settling times.
Occurrence of Unstable Transfer Function Models
Marlin (1995) has showed that a jacketed CSTR that is being used to perform a simple reaction gives USOPTD model that contains two unstable complex conjugate poles and a negative zero, when the model equations are linearized around an unstable operating point. Jacobsen (1999) studied the dynamics of reactor-separator networks and has shown that the transfer function model between the composition of the distillate and the recycle ratio of the distillation column results in an unstable second-order model with one unstable pole and one unstable zero. Huang and Chen (1999) have shown that the dynamics of an unstable Continuous Stirred Tank Reactor (CSTR), that is being used to perform an exothermic reaction can be modeled by a second order unstable model with one Right Half Plane (RHP) pole and time delay. Seki et al. (2001) have studied an unstable transfer function model of the gas phase polyolefin reactor, where the number of open-loop RHP poles varies from one to two, depending on the operating conditions. Bequette (2003) has considered a CSTR that was performing a simple reaction and showed that the linearized model around the unstable operating point gives an USOPTD model with one unstable pole and one stable pole and a negative zero. Wang and Hwang (2005) have shown the transfer function relating to the reactor temperature to coolant flow rate in a jacketed CSTR at two operating points is USOPTD system with one RHP pole and a negative zero and at the third operating point, the transfer function model is USOPTD system with two RHP poles and a negative zero. Padma Sree and Chidambaram (2006) have considered the model equations of autocatalytic CSTR and the linearization of model equations around the unstable operating point resulting in USOPTD model with a dominant positive zero and two RHP complex conjugate poles.
1. Literature Review on Design of PID Controllers for Unstable Systems
The methods of designing PID controller for unstable SOPTD (Second Order systems Plus Time D day) systems are synthesis method (Padma Sree and Chidambaram, 2004; Seshagiri Rao and Chidambaram, 2006, 2007; Cho et al., 2014, Vanavil et al., 2013), IMC Intunal Model Control method (Lee et al., 2000; Padma Sree and Chidambaram, 2003; Shamsuzzoha and Lee, 2007, 2008a, 2008b, 2009; Krishna et al., 2012; Vu and Lee, 2013, Vanavil et al., 2014) and methods based on gain margin and phase margin specifications (Wang, 2014). Padma Sree and Chidambaram (2004, 2006) have derived PID parameters assuming third order closed loop transfer function model with a negative zero and time delay along with the process zero. From the closed loop transfer function, controller transfer function is obtained. First order Pade's approximation is used for time delay. Among the three closed loop time constants, two time constants are made equal and is a tuning parameter. The third time constant and the numerator zero are obtained by canceling the unstable poles in the numerator of controller transfer function (Gc) with the denominator of Gc . Thus a PID controller with a lag filter is obtained. Seshagiri Rao and Chidambaram (2007) also used third order closed loop transfer function model with second order numerator and time delay along with the process zero. First order Pade's approximation is used for time delay. The numerator time constants of the closed loop transfer function are obtained by canceling the unstable poles in the numerator of Gc with the denominator of Gc . Thus a PID controller with a lead lag filter is obtained. Cho et al. (2014) have derived PID parameters for USOPTD process assuming third order closed loop transfer function with second order numerator along with process time delay. They have used truncated Taylor series expansion for time delay to derive PID parameters. Vanavil et al. (2013) have used same closed loop transfer function as Seshagiri rao and Chidambaram (2007) and second order Pade's approximation is used for delay. This has resulted in PID controller with a second order lead and lag filter. Nominal and robust control performances are reported for this method.
Lee et al. (2000) have derived PID controller settings from IMC controller using Macclarin series. Padma Sree and Chidambaram (2003) have derived PID settings for USOPTD system with a positive zero using first order Pade's approximation in the process itself using IMC principles. Then IMC controller is designed and from IMC controller, PID controller parameters are obtained. The unstable poles of the process in the numerator of Gc are canceled with the denominator of Gc to get the unknown parameters. The controller is PID with a lead lag filter. Shamsuzzoha and Lee (2007) used ½ Pade's approximation to get the PID parameters from IMC controller. Shamsuzzoha and Lee (2008a, 2008b, 2009) have used first order Pade's approximation to derive the parameters of PID controller with a lead/ lag filter. Recently Vu and Lee (2013) have derived PID parameters for USOPTD system by using 3/1 Pade's approximation for time delay. This procedure yields PID controller with a lead/ lag filter.
Chidambaram and Padma Sree (2003) have designed PID controller for integrator plus time delay system using equating coefficient method. In this method, the corresponding coefficients of s3 , s2 and s1 of the numerator of the closed loop transfer function for servo problem are equated to that of the denominator to derive PID parameters. Padma sree and Chidambaram (2005) extended the method of Chidambaram and Padma Sree (2003) to improve the performance of PID controller for integrating systems with time delay. They have used two tuning parameters α1 and α2. The corresponding coefficients of s1 , s2 and s3 of the numerator of closed loop transfer function are equated to α1 , α2 and α3 times of that of the denominator respectively. Padma Sree and Chidambaram (2004b) have extended the equating coefficient method to unstable first order plus time delay system to design PID controller.
In the proposed work, equating coefficient method is extended to USOPTD systems. The tuning parameters α1 , α2 and α3 are obtained by optimizing the performance (ITAE for servo problem) using fminunc of Matlab. If USOPTD system contains a negative zero, PID controller is designed without a zero and while implementation PID controller along with a first order filter with the time constant equal to the numerator time constant of the process is used. If USOPTD system contains a positive zero, then controller is designed for the USOPTD system with effective time delay which is equal to the sum of time delay of the process and numerator time constant (by using approximation [1-ps]=e-ps) The designed controller is implemented on the actual process.
The paper is organized as follows. In section 2, the proposed method is given. Section 3 gives the details of performance and robustness evaluation and in section 4, simulation results of various transfer function models and nonlinear model equations of CSTR are given. The conclusions are given in last section.
2. Proposed Method
The transfer function of second order plus time delay system is given by,
A PID controller is considered to stabilize the process. The PID controller is given by,
The closed loop transfer function relating the output variable (y) to the set point ( yr ).
Substituting equation (1) and equation (2) in equation (3), the following equation for closed loop is obtained.
Where,
e-Ls in the denominator is written as
e-Ls in the numerator only shifts the response on time axis and not considered in the further analysis.
Equation (4) is written as,
Using Taylor series expansion for e0.5Ls and e- 0.5Ls
Where,
Substituting equation (10) and equation (11) in equation (9), 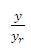 is expressed as the ratio of polynomials. Equating the corresponding co-efficient of s1 , s2 and s3 in the numerator polynomial with that of α1,α2 and α3 times the denominator, the following three linear equations are obtained.
is expressed as the ratio of polynomials. Equating the corresponding co-efficient of s1 , s2 and s3 in the numerator polynomial with that of α1,α2 and α3 times the denominator, the following three linear equations are obtained.
By tuning α1,α2 and α3 and solving these linear equations k1, K2 and k3 are obtained.
In the proposed work, α1,α2 and α3are selected in such a way that the resulting PID parameters yield minimum Integral Time weighted Absolute Error (ITAE) value for servo problem, i.e,the problem is formulated as an optimization problem and is solved using fiminunc of Matlab. The values anigned for α1,α2 and α3 are selected as 1.5, 0.9α1 and 0.9α1. The optimization routine converged for these initial guess values.
3. Performance Index, Robustness and Input Usage
The PID controller is designed to stabilize the system and to provide good set point tracking and good disturbance rejection with robustness to the parameter uncertainty. To compare the efficiency of the PID controller, three criterions are studied namely performance index, stability/ robustness and input usage.
3.1 Performance Index
The following performance indices are used to compare the performance of the controller designed by the proposed method with the other recently reported methods. ISE 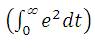 penalizes large errors; IAE
penalizes large errors; IAE 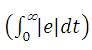 treats all errors equally and Integral Time weighted Absolute Error
treats all errors equally and Integral Time weighted Absolute Error 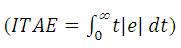 penalizes the errors that exist for long time (Seborg et al., 2004). Here, e is the error which is the difference between set point and the output variable. In the proposed work, ITAE is used as performance measure as many authors in the literature reported the performance in terms of ITAE. The smaller value of any one of the indices indicates that particular method is performing better than other methods.
penalizes the errors that exist for long time (Seborg et al., 2004). Here, e is the error which is the difference between set point and the output variable. In the proposed work, ITAE is used as performance measure as many authors in the literature reported the performance in terms of ITAE. The smaller value of any one of the indices indicates that particular method is performing better than other methods.
3.2 Robustness and Stability
To measure the robustness and stability of the PID controller designed by proposed method, maximum magnitude of sensitivity function is used. Sensitivity function is given by,
The amplitude ratio of S is given by,
Then the maximum value of amplitude ratio (Ms) gives the measure of robustness. The stability of the controller is based on the value of Ms. More the value of Ms, the controller is more susceptible to parameter uncertainties. Lesser the value, the controller is said to be more stable to parameter uncertainties. In general, for stable systems Ms value between 1.2 to 2 gives good robustness. However for unstable systems this value is greater than or equal to 2 (Seborg et al.(2004)). By using Ms value, lower bound for gain margin value is given by,
3.3 Input Usage
The manipulated variable is also a good measure of performance of the controller. Total Variation (TV), is a good measure of smoothness of the input to the process. Lesser the value of TV, the input is found to be smoother. TV is calculated as,
Where, ui is the input to process or manipulated variable at the ith instant (Shamsuzzoha and Lee, 2008).
4. Simulation Results and Discussion
Simulation results on various transfer function models and the nonlinear model equations of jacketed CSTR are given in this section to demonstrate the superiority of the proposed method. The performance of the proposed controller is compared with that of the controllers designed by recently reported methods (Cho et al., 2014; Nasution et al., 2011; Seshagiri Rao and Chidambaram, 2007 and Krishna et al., 2014) in terms of ITAE. The regulatory performance of the proposed controller is superior to that of the controllers designed by literature reported methods. However, the proposed controller is less robust as it gives slightly large Ms value when compared with the other controllers.
4.1 Case Study 1
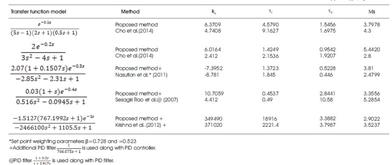
The transfer function model 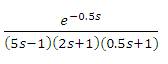 (Cho et al., 2014) is considered. Cho et al. (2014) used model reduction technique to reduce it to Second order Plus Time Delay (SOPTD) model,
(Cho et al., 2014) is considered. Cho et al. (2014) used model reduction technique to reduce it to Second order Plus Time Delay (SOPTD) model,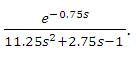 . The SOPTD model used for the PID controller design by the present method is
. The SOPTD model used for the PID controller design by the present method is 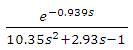 (Nasution et al., 2011; Vu and Lee, 2013). The PID parameters obtained by the present method (converged values of α1,α2 and α3 are 1.4889, 1.3719 and 0.6974) and that is given by Cho et al. (2014) as reported in Table 1. A unit step change in load is given at time t=0 sec and unit step change in set point is given at time t=25 sec. The regulatory and servo performance of the proposed controller and the controller designed by Cho et al. (2014) are shown in Figure 1. Cho et al. (2014) have used a set point filter to reduce overshoot in the servo response. Therefore, set point weighting parameter (b=0.638) is calculated by using equating coefficient method (Padma Sree and Chidambaram, 2004c) which is used with the proposed controller to reduce overshoot in the servo response. The performance of set point weighted PID controller is also shown in Figure 1.
(Nasution et al., 2011; Vu and Lee, 2013). The PID parameters obtained by the present method (converged values of α1,α2 and α3 are 1.4889, 1.3719 and 0.6974) and that is given by Cho et al. (2014) as reported in Table 1. A unit step change in load is given at time t=0 sec and unit step change in set point is given at time t=25 sec. The regulatory and servo performance of the proposed controller and the controller designed by Cho et al. (2014) are shown in Figure 1. Cho et al. (2014) have used a set point filter to reduce overshoot in the servo response. Therefore, set point weighting parameter (b=0.638) is calculated by using equating coefficient method (Padma Sree and Chidambaram, 2004c) which is used with the proposed controller to reduce overshoot in the servo response. The performance of set point weighted PID controller is also shown in Figure 1.

Figure 1. The Response for the System 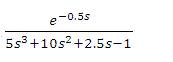
The proposed controller gives less Ms value compared to the controller designed by Cho et al. (2014) indicating that the proposed controller is more robust compared to Cho et al. (2014) controller. Total Variation (TV) value indicates the smoothness of the controller. The proposed controller is less smooth when compared to the controller by Cho et al. (2014). Since the method is based on optimization of ITAE, it gives best performance and the controller is less robust
4.2 Case Study 2
The transfer function model 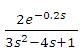 (Cho et al., 2014) is considered. The PID settings for the proposed method (converged values of α1,α2 and α3 are 1.0565, 1.9822, 0.7982) and the IMC method (Cho et al., 2014) are given in Table 2. A unit step change in the load is given at time t=0 sec and a unit step change in set point is given at time t= 10 sec. The regulatory and servo response of the system is shown in Figure 2. The regulatory and servo performance of the controller designed by Cho et al. (2014) is also shown in Figure 2. The proposed controller shows the superior performance for regulatory problem.
(Cho et al., 2014) is considered. The PID settings for the proposed method (converged values of α1,α2 and α3 are 1.0565, 1.9822, 0.7982) and the IMC method (Cho et al., 2014) are given in Table 2. A unit step change in the load is given at time t=0 sec and a unit step change in set point is given at time t= 10 sec. The regulatory and servo response of the system is shown in Figure 2. The regulatory and servo performance of the controller designed by Cho et al. (2014) is also shown in Figure 2. The proposed controller shows the superior performance for regulatory problem.
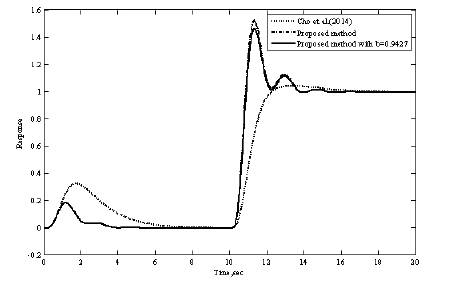
Figure 2. The Response for the System 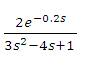
The servo response of the proposed controller is improved by using a set point weighted PID controller with a set point weighting parameter b= 0.9427 (equating coefficient method, Padma Sree and Chidambaram, 2004c). Cho et al. (2014) have used set point filter such that the closed loop response is similar to that of first order system with time delay. The servo response of the controller designed by Cho et al. (2014) is better than the proposed controller. The Ms value of the proposed controller is large compared to the controller designed by Cho et al. (2014) indicating that it is more robust and smooth compared to proposed controller. The regulatory response of the proposed controller is superior to the controller designed by Cho et al. (2014)
4.3 Case Study 3
The transfer function model (Nasution et al., 2011) is considered. The PID settings for the proposed method is,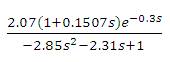 (converged values of α1,α2 and α3 are 1.3440, 1.3043 and 0.6412) and the optimal H2IMC-PID (Intunal Model Control Propostional Integral Derivative) method (Nasution et al., 2011) are given in Table 1. A unit step change in the set point is given at time t=0 sec and a unit step change in load is given at time t= 10 sec. The servo and regulatory response of the system is shown in Figure 3. The servo and regulatory performance of the controller designed by Nasution et al. (2011) is also shown in Figure 3. The proposed controller shows superior performance for regulatory problem. The servo response of the proposed controller is improved by using a set point weighted PID controller with a set point weighting parameter b= 0.716. Nasution et al. (2011) used to set point weighting parameters β=0.728 and γ=0.523, as such that the closed loop servo response gives less overshoot and the response is fast. The servo response of the controller designed by Nasution et al. (2011) is better than the proposed controller. The Ms value of the proposed controller is large compared to the controller designed by Nasution et al. (2011), indicating that it is more robust and smooth compared to proposed controller. The controller functioning is smooth for the proposed method compared to H2IMC method for servo problem.
(converged values of α1,α2 and α3 are 1.3440, 1.3043 and 0.6412) and the optimal H2IMC-PID (Intunal Model Control Propostional Integral Derivative) method (Nasution et al., 2011) are given in Table 1. A unit step change in the set point is given at time t=0 sec and a unit step change in load is given at time t= 10 sec. The servo and regulatory response of the system is shown in Figure 3. The servo and regulatory performance of the controller designed by Nasution et al. (2011) is also shown in Figure 3. The proposed controller shows superior performance for regulatory problem. The servo response of the proposed controller is improved by using a set point weighted PID controller with a set point weighting parameter b= 0.716. Nasution et al. (2011) used to set point weighting parameters β=0.728 and γ=0.523, as such that the closed loop servo response gives less overshoot and the response is fast. The servo response of the controller designed by Nasution et al. (2011) is better than the proposed controller. The Ms value of the proposed controller is large compared to the controller designed by Nasution et al. (2011), indicating that it is more robust and smooth compared to proposed controller. The controller functioning is smooth for the proposed method compared to H2IMC method for servo problem.
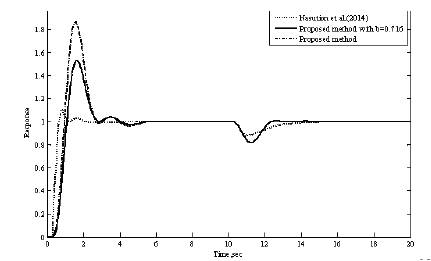
Figure 3. The Response for the System 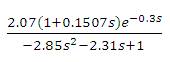
4.4 Case Study 4
The transfer function model (Seshagiri Rao and Chidambaram, 2007) is considered. The PID settings for the proposed method (converged values of α1,α2 and α3 are 0.3923, 1.0237 and 0.5592) and the direct synthesis method (Seshagiri Rao and Chidambaram, 2007) are given in Table 1. A unit step change in the set point is given at time t=0 sec and a unit step change in load is given at time t= 15 sec. The servo and regulatory response of the system is shown in Figure 4. The servo and regulatory performance of the controller designed by Seshagiri Rao and Chidambaram (2007) is also shown in Figure 4. The proposed controller shows the superior performance for regulatory problem. The servo and regulatory response of the controller designed by proposed method is superior to the controller designed by direct synthesis method (Seshagiri Rao and Chidambaram, 2007) and is better than the proposed controller in terms of ITAE. The functioning of proposed controller is smooth when compared with the controller designed by direct synthesis method. The Ms value of the proposed controller is less compared to the controller designed by Seshagiri Rao and Chidambaram (2007) indicating that it is more robust.
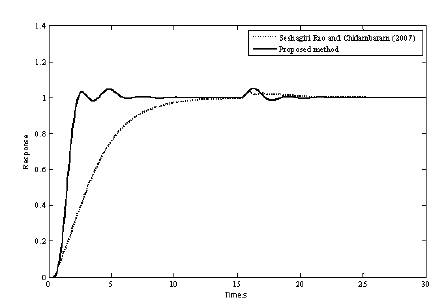
Figure 4. The Response for the System 
4.5 Case Study 5: Jacketed CSTR
Consider a jacketed CSTR carrying first order irreversible exothermic reaction (Wright and Kravaris, 2006) and the model equations are,
The process parameters are given in Table 3. The above nonlinear equations [equation (24) equation (25)] are linearized around unstable operating point C As =3.734 K mol/m3 , Ts = 344 K and Tjs = 317.4 K and transfer function model is given by
Rearranging
Simplifying equation (28), the following transfer function model is obtained. A measurement time delay of 1 s is considered.
PID controller settings for the proposed method (converged values of α1,α2 and α3are 1.0001, 1.3472 and 0.5891) and the Krishna et al. (2012). are given in Table 1. The servo performance of the proposed controller for a step change in reactor temperature from 344 K to 346 K is shown in Figure 5. In the same figure, the servo response of the controller designed by Krishna et al. (2012). is also shown. The response of the proposed controller is superior to that of the controller designed by Krishna et al. (2012). The performance in terms of ITAE is given in Table 2. The regulatory response of the proposed controller for step change in TJ from 317.4K to 310K is shown in Figure 6 for both controllers (refer to Table 2). The proposed controller gives superior performance compared to the controller designed by Krishna et al. (2012).
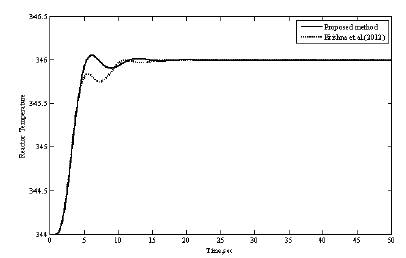
Figure 5. The Servo Response for the Jacketed CSTR for the Change in Reactor Temperature from 344 K to 346 K (Nonlinear Model)
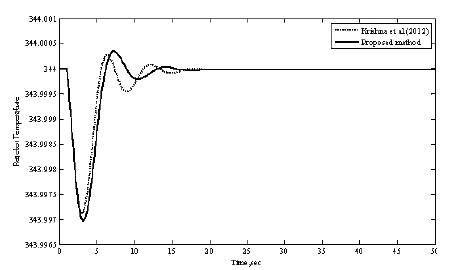
Figure 6. The Regulatory Response for the Jacketed CSTR for the Change in Jacket Temperature from 317.4 K to 310 K (Nonlinear Model
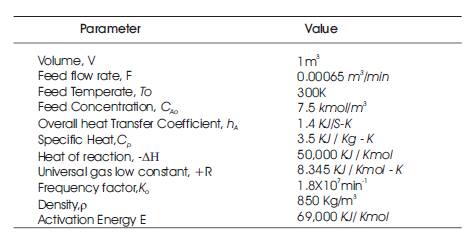
Table 3. Parameter Values for Jacketed CSTR
The Ms value of the proposed controller is less than that of the controller designed by Krishna et al. (2012). indicating that the proposed controller is more robust. The smoothness of the controller action is given in terms of TV value which is less than the controller designed by Krishna et al. (2012). The functioning of the proposed controller is smooth compared to the controller designed by Krishna et al. (2012).
Conclusion
The equating coefficient method of designing PID controllers for stable/unstable FOPTD systems and integrating time delay systems is extended to unstable SOPTD systems. The tuning parameters α1,α2 and α3 are selected by minimizing ITAE for servo problem. The regulatory performance of the controller is superior to the recently reported methods. The servo response of the proposed controller is comparable to that of the existing methods. The controller is robust for parameter uncertainty. The proposed controller gives good regulator y performance for various transfer function models and jacketed CSTR carrying an irreversible first order reaction.
References
[1]. Bequette B. W, (2003). “Process Control: Modeling, Design and Simulation”, Prentice Hall, India.
[2]. Chidambaram M., (1997). “Control of Unstable Systems: A Review”, Journal of Energy, Heat and Mass Transfer, Vol. 19, pp. 49-57.
[3]. Chidambaram M and R. Padma Sree, (2003). “A Simple Method of Designing PI / PID Controllers for Integrator/Dead Time Processes”, Computer and Chemical Engineering, Vol . 27, pp. 211-215.
[4]. Cho W., Lee J., and Edgar T. F, (2014). “Simple Analytic Proportional-Integral-Derivative (PID) Controller Tuning Rules for Unstable Processes”, Industrial and Engineering Chemistry Research, Vol. 53, pp. 5048-5054.
[5]. Huang H. P and C. C. Chen, (1999). “Auto Tuning of PID Controllers for Second Order Unstable Systems Having Dead Time”, Journal on Chemical Engineering, Vol.32, pp. 568-579.
[6]. Marlin T. E., (1995). “Process Control: Designing Processes and Control Systems for Dynamic Performance”, McGraw- Hill, New York.
[7]. Nasution A. A, J. C Jung, and H. P Huang., (2011). 2 “Optimal H IMC-PID Controller with Set Point Weighting for Time Delayed Unstable Processes”, Industrial and Engineering Chemistry Research, Vol. 50, pp. 4567-4578.
[8]. Jacobsen E. W., (1999). “On the Dynamics of Integrated Plants Non-minimum Phase Behavior”, Journal on Process Control, Vol. 9, pp. 439-451.
[9]. Krishna D, K. Suryanarayana, G. Aparna and R. Padma Sree, (2012). “Tuning of PID controllers for Unstable Stirred Tank Reactors”, International Journal of Applied Science and Engineering, Vol.10, pp. 1-18.
[10]. Lee Y, J. Lee and S. Park, (2000). “PID Controller Tuning for Integrating and Unstable Processes with Time Delay”, Chemical Engineering Science, Vol. 55, pp.3481- 3493.
[11]. Padma Sree R. and M. Chidambaram, (2003). “IMC Controller Design for Unstable with a Zero”, Proceedings of International Conference on Chemical and Bio-chemical Engineering, pp. 843-850.
[12]. Padma Sree R. and M. Chidambaram, (2004a). “Control of Unstable Reactor with an Unstable Zero”, Indian Chemical Engineering, Vol. 46, pp. 21-26.
[13]. Padma Sree, R., M.N. Srinivas and M. Chidambaram, (2004b). “A Simple Method of Tuning PID Controllers for Stable and Unstable FOPTD Systems”, Computer and Chemical Engineering, Vol. 28, pp. 2201-2218.
[14]. Padma Sree, R. and M. Chidambaram, (2004c). “Simple Method of Calculating Set Point Weighting Parameter for Unstable Systems with a Zero”, Computer and Chemical Engineering, Vol. 28, PP. 2433-2437
[15]. Padma Sree R and M. Chidambaram, (2005). “Simple and Robust Method of Tuning PID Controller for Integrator/ Dead Time Process”, Journal of Chemical Engineering, Vol. 38, pp .113-119.
[16]. Padma Sree R. and M. Chidambaram, (2006). “Control of Unstable Systems”, Narosa Publishing House, New Delhi.
[17]. Seborg D. E., T. F. Edgar and D. A. Mellichamp, (2004). “Process Dynamics and Control”, John Wiley and Sons, New York.
[18]. Seki H., M. Ogawa and M. Ohshima, (2001). “PID Temperature Control of an Unstable Gas –phase Polyolefin Reactor”, Journal on Chemical Engineering, Vol. 34, pp. 1415-1422.
[19]. Seshagiri Rao A. and M. Chidambaram, (2007). “Control of unstable Processes with Two RHP Poles, a Zero and Time Delay”, Asia-Pacific Journal of Chemical Engineering, Vol. 1 ,No.1-2, pp. 63-69.
[20]. Seshagiri Rao, A and M. Chidambaram, (2006). “Enhanced Two-Degrees-of-Freedom Control Strategy for Second-Order Unstable Processes with Time Delay”, Industrial and Engineering Chemistry Research, Vol. 45, pp. 3604-3614.
[21]. Shamsuzzoha M and M. Lee, (2007). “Analytical Controller Design of Integrating and First Order Unstable th Time Delay Process”, 8 International IFAC Symposium on Dynamics and Control of Process Systems, Vol.2, pp. 397- 402.
[22]. Shamsuzzoha M. and M. Lee, (2008a). “Design of Advanced PID Controller for Enhanced Disturbance Rejection of Second-order Processes with Time Delay”, AIChE Journal, Vol. 54, pp. 1526 .
[23]. Shamsuzzoha M. and M. Lee, (2008b). “Analytical Design of Enhanced PID Filter Controller for Integrating and First Order Unstable Processes with Time Delay”, Chemical Engineering and Science, Vol. 63, pp. 2717.
[24]. Shamsuzzoha M. and M. Lee, (2009). “Enhanced Disturbance Rejection for Open-loop Unstable Process with Time Delay”, ISA Transactions, Vol. 48, pp. 237-244.
[25]. Wang Y.J., (2014). “Determination of all Feasible Robust PID Controllers for Open-loop Unstable Plus Time Delay Processes with Gain Margin and Phase Margin Specifications”, ISA Transactions, Vol. 53, pp. 628–646.
[26]. Wang L.W. and S.H. Hwang, (2005). “Identification and Control of Unstable Processes of Three Dynamic Types”, Chemical Engineering and Communication, Vol. 192,No.1, pp. 34-61.
[27]. Vu T.L.U and M.A. Lee, (2013). “A Unified Approach to the Design of Advanced Proportional-Integral-Derivative Controllers for Time-delay Processes”, Korean Journal on Chemical Engineering, Vol. 30, No.3, pp. 546-558.
[28]. Vanavil B., K. Krishna Chaitanya and A. Seshagiri Rao, (2013). “Improved PID Controller Design for Unstable Time Delay Processes Based on Direct Synthesis Method and Maximum Sensitivity”, International Journal of Systems Science, pp.1-17.
[29]. Vanavil B., A. V. N. L. Anusha, M. Perumalsamy and A. Seshagiri Rao, (2014). “Enhanced IMC-PID Controller Design with Lead-Lag Filter for Unstable and Integrating Processes with Time Delay”, Chemical Engineering and Communication, Vol. 201, pp. 1468–1496.
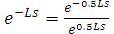 and it is expanded using Taylor series expansion upto four terms both in the numerator and denominator.This makes the numerator and denominator as polynomial of s. The time delay term in the numerator shifts the response on time axis and is not considered in the design problem. By equating the corresponding coefficients of s, s2 and s3 in the numerator with α1 , α2 , and α3 times that of the denominator; three linear equations are formulated and solved for the PID controller parameters. In the proposed work, the coefficients α1 , α2 , and α3 are obtained by minimizing Integral Time weighted Absolute Error (ITAE) for servo problem using fminunc of Matlab. Simulation results on various transfer function models and on the nonlinear model equations of jacketed CSTR (Continuous Stirred Tank Reactor) carrying out first order exothermic reaction are given to demonstrate the effectiveness of the proposed method. The smooth functioning of the controller is expressed interms of total variation. The controller performance is expressed in terms of ITAE. Nominal control performance of the proposed method is better than the existing methods.
and it is expanded using Taylor series expansion upto four terms both in the numerator and denominator.This makes the numerator and denominator as polynomial of s. The time delay term in the numerator shifts the response on time axis and is not considered in the design problem. By equating the corresponding coefficients of s, s2 and s3 in the numerator with α1 , α2 , and α3 times that of the denominator; three linear equations are formulated and solved for the PID controller parameters. In the proposed work, the coefficients α1 , α2 , and α3 are obtained by minimizing Integral Time weighted Absolute Error (ITAE) for servo problem using fminunc of Matlab. Simulation results on various transfer function models and on the nonlinear model equations of jacketed CSTR (Continuous Stirred Tank Reactor) carrying out first order exothermic reaction are given to demonstrate the effectiveness of the proposed method. The smooth functioning of the controller is expressed interms of total variation. The controller performance is expressed in terms of ITAE. Nominal control performance of the proposed method is better than the existing methods.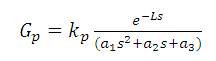

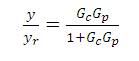

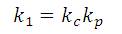
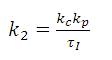
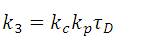
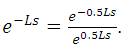

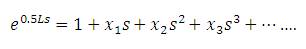

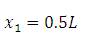
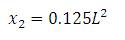
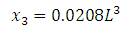
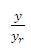 is expressed as the ratio of polynomials. Equating the corresponding co-efficient of s1 , s2 and s3 in the numerator polynomial with that of α1,α2 and α3 times the denominator, the following three linear equations are obtained.
is expressed as the ratio of polynomials. Equating the corresponding co-efficient of s1 , s2 and s3 in the numerator polynomial with that of α1,α2 and α3 times the denominator, the following three linear equations are obtained.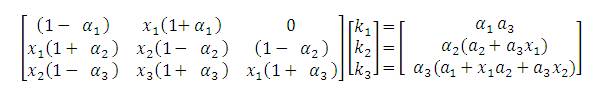
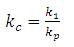
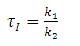
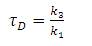
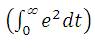 penalizes large errors; IAE
penalizes large errors; IAE 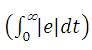 treats all errors equally and Integral Time weighted Absolute Error
treats all errors equally and Integral Time weighted Absolute Error 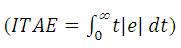 penalizes the errors that exist for long time
penalizes the errors that exist for long time 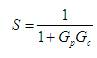

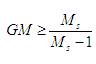

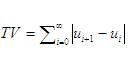
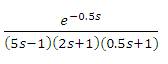
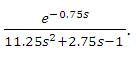 . The SOPTD model used for the PID controller design by the present method is
. The SOPTD model used for the PID controller design by the present method is 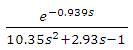

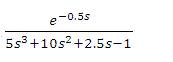
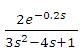

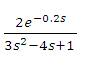
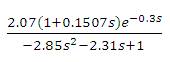 (converged values of α1,α2 and α3 are 1.3440, 1.3043 and 0.6412) and the optimal H2IMC-PID (Intunal Model Control Propostional Integral Derivative) method
(converged values of α1,α2 and α3 are 1.3440, 1.3043 and 0.6412) and the optimal H2IMC-PID (Intunal Model Control Propostional Integral Derivative) method