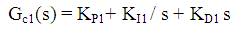
This paper presents the effects of load parameters and their variations on power system frequency and tie-line power. In this study the authors have selected two area thermal power system with Integral (I) and PSO-PID (Practice Swarn Optimization-Proportional-Integral Derivative) controllers. From the mathematical modelling of power system, frequency is a function of power system parameters and small changes in these parameters lead to small deviations in the system frequency and tie-line power. In case of extreme ends of parameters, even for small changes in load power there will be a chance of instability in overall power system. This paper deals with stable case for different parameter variations. Simulations are carried out in MATLAB/SIMULINK software.
Main role of Automatic Generation Control (AGC) is to maintain the system at their scheduled values during normal operating period [1]. The problem of controlling the real power output of generating units in response to changes in system frequency and tie-line power interchange within specified limits is known as Load Frequency Control (LFC). It is generally regarded as a part of Automatic Generation Control (AGC) and is very important in the operation of power systems [2].
The LFC is fundamentally for the problem of an instantaneous mismatch between the generation and demand of active power [3]. The objective of Load Frequency Control (LFC) is to minimize the transient deviations in these variables and to ensure their steady state values to be zero.
Mismatching between generated power and load demand leads to change in the frequency. In actual power system operations, the load is changing continuously and randomly, resulting in the deviations of load frequency and the tie-line power between any two areas from scheduled generation quantities. As technology has become so advanced that every system should work with stability and accuracy in order to get the efficient response, but at the same time due to complexity of systems and randomly changing load conditions, sometimes the stability could not be maintained. The fluctuation of load in these systems are very common, which can reduce their efficiency or may damage the system but it can be prevented by the use of different controllers in order to provide the automatic generation control or Load Frequency Control [4].
The most commonly used controllers are conventional I and PID controllers. The conventional PID control schemes will not reach a high of control performances [12]. Since the dynamic behaviour even for a reduced mathematical model of a power system is usually nonlinear and governed by strong cross-couplings of the input variables, special care has to be taken for the design of the controllers. For this reason, recently, a lot of artificial intelligence based robust controllers such as genetic algorithm, fuzzy logic and neural networks are used for PID controller parameters tuning in LFC.
Since, Particle Swarm Optimization algorithm is an optimization method that finds the best parameters for controller in the uncertainty area of controller parameters it has been used in almost all sectors of industry and science [11].
In recent years, most of the research is done in the aspect of different controllers in the area of automatic generation control for random load changes, but in this paper, a separate aspect of AGC is discussed [5]. This paper illustrates the effect of load parameter variations of two area power system in presence of conventional I as well as PSO-PID controllers.
It is observed that there is a lot of change in behaviour in the frequency response without controller and with controllers (I and PSO-PID) at fixed load parameters as well as variable load parameters. Simulations are carried out in MATLAB/ SIMULINK software. The transient responses of system with different controllers (I and PSO-PID) are compared to establish their effectiveness.
In the view of above, objectives of this work are as follow:
The control system that is used in this paper is two area power system [1]. The linearized model of the controlled system is shown in Figure 1 and system parameters are given in Appendix A. In the model, ΔPL1 is step load changes in area 1. Δf1 is frequency deviation in area 1, Δf2 is frequency deviation in area 2 and ΔPtie is the tie-line power deviation. In two area system considered for study, the PID controllers with following structure is used.
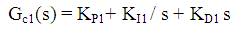
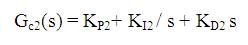
Where,
KP is proportional gain
KI is integral gain and
KD is derivative gain respectively
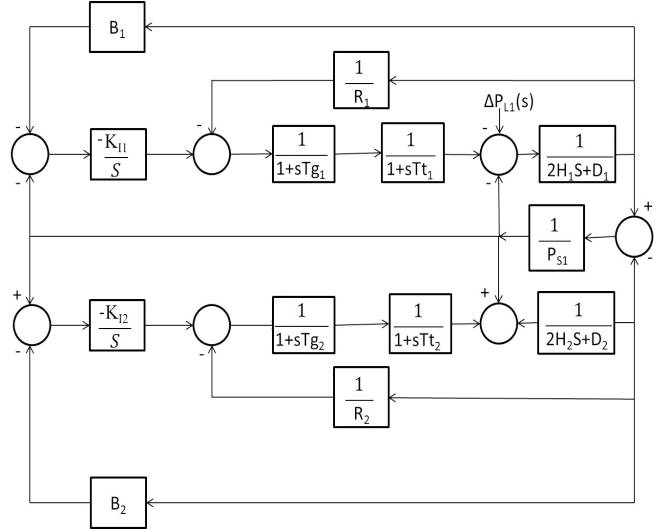
Figure 1. Linearized Model of Two Area System Model
Particle Swarm Optimization (PSO) is a population (swarm) based stochastic optimization algorithm which was first introduced by Kennedy and Eberhart in 1995 [7]. It can obtain high quality solutions within shorter calculation time and stable convergence characteristics with PSO algorithm than other stochastic methods such as genetic algorithm.
Particle Swarm Optimization uses particles which represent potential solutions of the problem. Each particles fly in search space at a certain velocity which can be adjusted in light of certain velocity, in light of proceeding flight experiences. The projected position of ith particle of the swarm Xi, and the velocity of this particle Vi at (i+1) th iteration are defined by the following equations in this study [10].
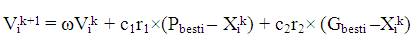
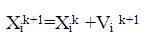
Where,
i=1,…... n and n is the size of the swarm,
c1 and c2 are positive constants
r1 and r2 are random numbers in [0,1],
k determines the iteration number,
Pbesti represents the previous best of the ith particle ,
Gbesti represents the best among all the particles in the swarm.
In this velocity updating process, the values of parameters such as ω, c1 and c2 should be determined in advance. In general, the weight ω is set according to the following equation (5) [8].
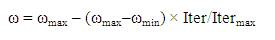
Where,
ωmax , ωmin initial and final weights,
Itermax maximum iteration number
Iter current iteration number.
Main objective of the work is to minimize peak and settling time, so objective function is chosen as the Integral Square Error (ISE) [6].
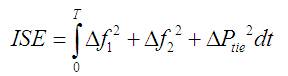
The algorithm of PSO : [9]
At the end of the iterations, the best position of the swarm will be the solution of the problem i.e., Gbest values will give optimal control parameters for PID controller.
In this proposed work, two area thermal power system have been developed by using Integral and PSO-PID controllers to illustrate the performance of load frequency control using MATLAB/SIMULINK software. Several types of Simulink models for different cases are developed with those controllers to obtain better dynamic behaviour. Frequency and tie-line power deviation plots for different parameter variations (D & ΔPL ) are obtained as shown in figures.
In this case the dynamic response plots without any controller are given. Two area thermal power system as shown in Figure 2 is studied for variable load damping coefficient (i.e., D=0.1,0.6 & 3) and variable load change ΔPL (10%, 30% & 50%) without any controller. Simulation results of frequency and tie-line power responses are given below.
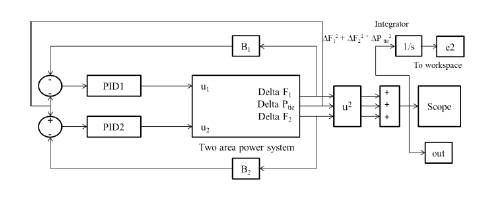
Figure 2. Implementation of PSO Algorithm for Two Area System.
a) Dynamic performances at load damping coefficient 0.1 are given below in Figures 3, 4 and 5.
b) Dynamic performances at load damping coefficient 0.6 are given below in Figures 6, 7 and 8.
c) Dynamic performances at load damping coefficient 3 are given below in Figures 9,10 and11.
Figures 3-11 show the dynamic responses for AGC of two area system without any controller, having different load parameters. To eliminate steady state error presented in dynamic responses, integral controller (I) is used. Dynamic responses with integral controller is given below.
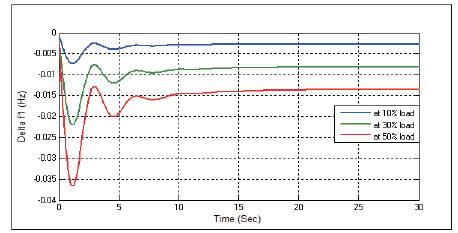
Figure 3. Change in Frequency Δf1 without any Controller at D=0.1
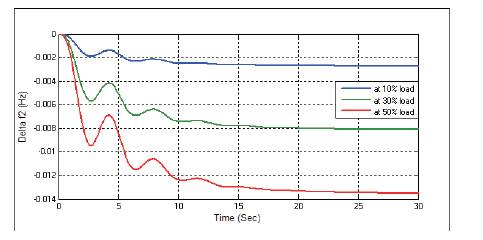
Figure 4. Change in Frequency Δf2 without any Controller at D=0.1
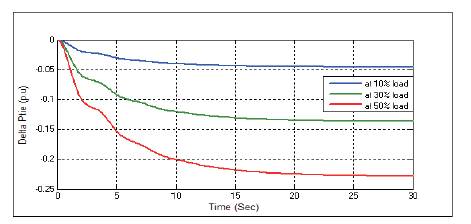
Figure 5. Change in Tie-line Power ΔPtie Without any Controller at D=0.1.
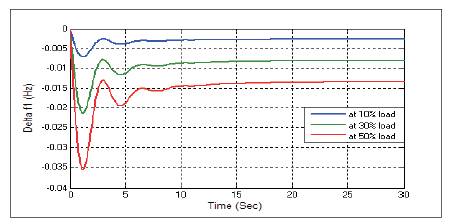
Figure 6. Change in Frequency Δf1 Without any Controller at D=0.6
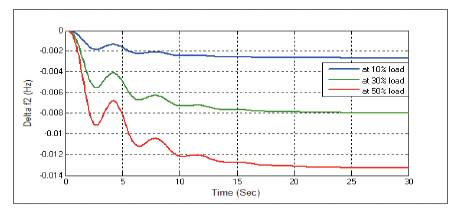
Figure 7. Change in Frequency Δf2 without any Controller at D=0.6
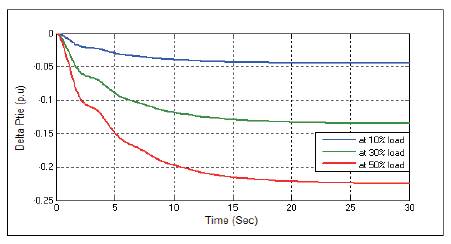
Figure 8. Change in Tie-line Power ΔPtie Without any Controller at D=0.6
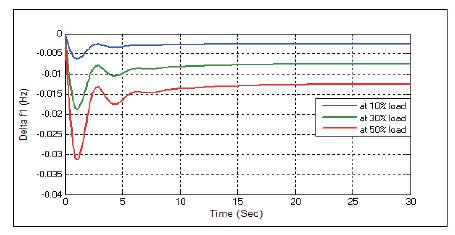
Figure 9. Change in Frequency Δf1 Without any Controller at D=3

Figure 10. Change in Frequency Δf2 Without any Controller at D=3
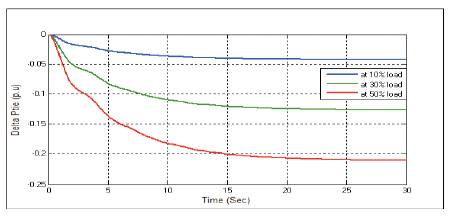
Figure 11. Change in Tie-line Power ΔPtie Without any Controller at D=3
In this case the dynamic performance plots with integral (I) controller is analysed when one of the load parameter i.e. damping coefficient (D) is a variable (i.e., D=0.1,0.6 & 3) with variable load change ΔPL , (10%, 30% & 50%) with integral controller. Simulation results of frequency and tieline power responses are given below.
a) Dynamic performances at load damping coefficient 0.1 are given below in 12,13 and14.
b) Dynamic performances at load damping coefficient 0.6 are given below in 15,16 and17.
c) Dynamic performances at load damping coefficient 3 are given below in 18,19 and 20.
Figures 12-20 show the dynamic responses for AGC of two area system in the presence of integral controller with different load parameters. To minimize the peak magnitude and settling time presented in dynamic responses, PSO tuned PID controller is used. Dynamic responses with PSO tuned PID controller is given below.
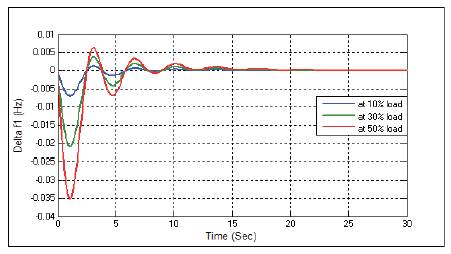
Figure 12. Change in Frequency ΔfL with Integral Controller at D=0.1

Figure 13. Change in Frequency Δf2 with Integral Controller at D=0.1.
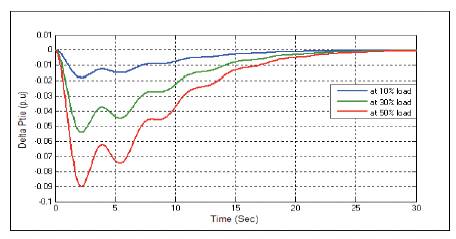
Figure 14.Change in Tie-line Power ΔPtie with Integral Controller at D=0.1.
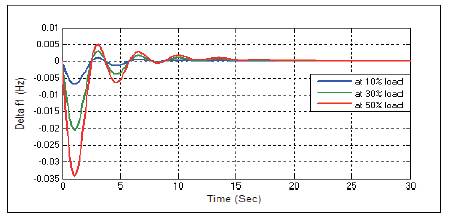
Figure 15. Frequency Response Δf1 with Integral Controller at D=0.6
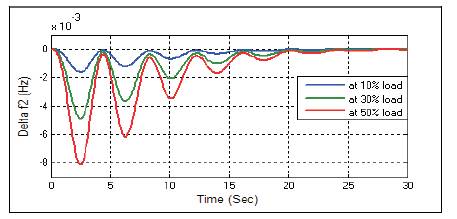
Figure 16. Change in Frequency Δf2 with Integral Controller at D=0.6
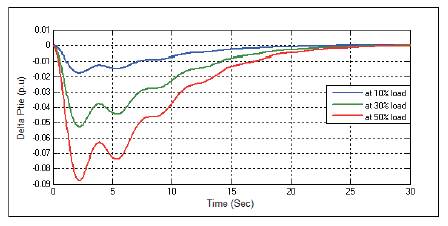
Figure 17.Change in Tie-line Power ΔPtie with Integral Controller at D=0.6
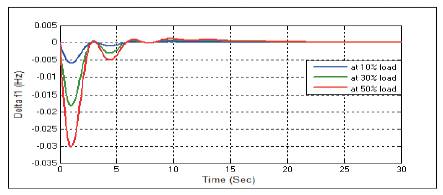
Figure 18. Change in Frequency Δf1 with Integral Controller at D=3

Figure 19. Change in Frequency Δf2 with Integral Controller at D=3

Figure 20. Change in Tie-line power ΔPtie with Integral Controller at D=3
In this case the dynamic response plots with PSO-PID controller is analysed when one of the load parameter i.e. damping coefficient (D) is a variable with variable load change ΔPL .The simulation plots at different values of D (i.e.,D=0.1,0.6 and 3) with variable load change ΔPL . (10%, 30% & 50%) with PSO-PID controller is studied. Simulation results of frequency and tie-line power responses are given below.
a) Dynamic performances at load damping coefficient 0.1 are given below in 21,22 and 23.
b) Dynamic performances at load damping coefficient 0.6 are given below in 24,25 and 26.
c) Dynamic performances at load damping coefficient 3 are given below in 27,28 and 29.
Figures 21-29 show the dynamic responses for AGC of two area system in the presence of PSO-PID controller with different load parameters. Dynamic responses for AGC of two area power system with PSO tuned PID controller having different load parameters offers minimum Peak magnitude and settling time.
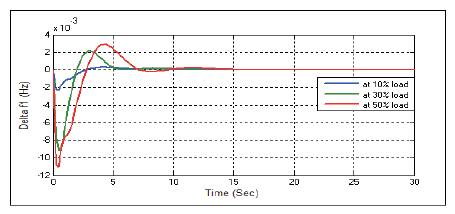
Figure 21. Frequency Response Δf1 with PSO-PID Controller at D=0.1.
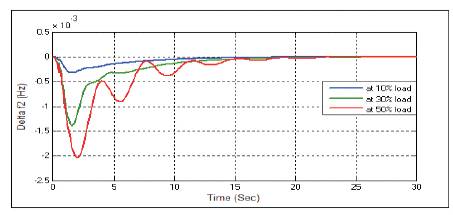
Figure 22. Change in Frequency Δf2 with PSO-PID Controller at D=0.1
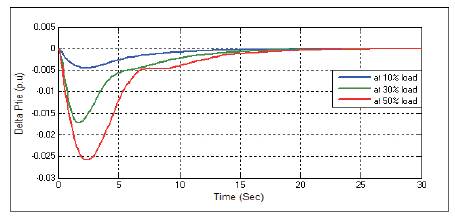
Figure 23. Change in Tie-line Power ΔPtie with PSO-PID Controller at D=0.1
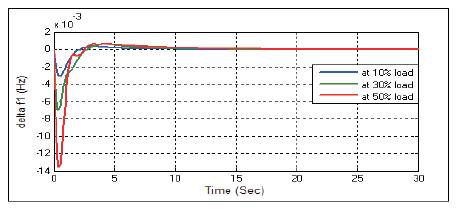
Figure 24. Frequency Response Δf1 with PSO-PID Controller at D=0.6
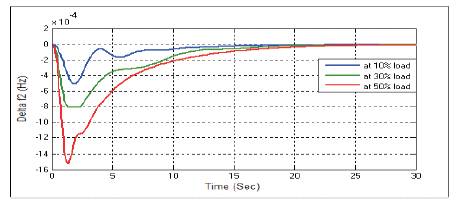
Figure 25. Change in Frequency Δf2 with PSO-PID Controller at D=0.6
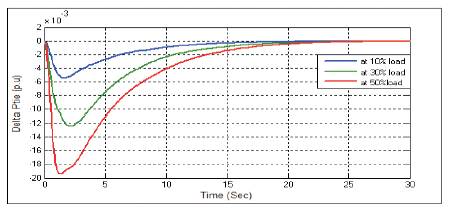
Figure 26. Change in Tie-line Power ΔPtie with PSO-PID Controller at D=0.6
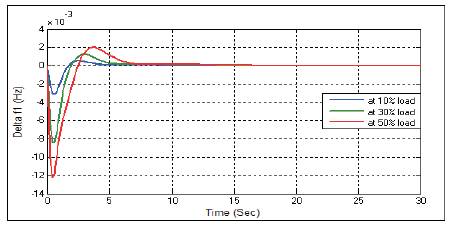
Figure 27. Frequency Response Δf1 with PSO-PID Controller at D=3
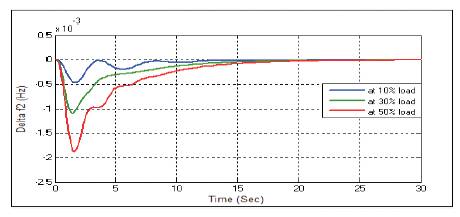
Figure 28. Change in Frequency Δf2 with PSO-PID Controller at D=3
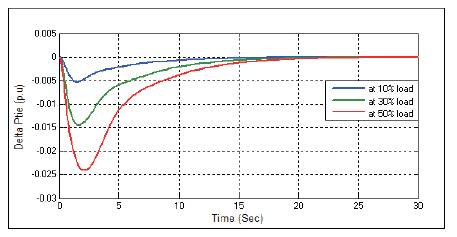
Figure 29. Change in Tie-line Power ΔPtie with PSO-PID Controller at D=3
In this paper, PSO-PID has been investigated for load frequency control of a two area power system. For this purpose, first, to obtain the PID controller parameters, PSO algorithm is used. It has been shown that the proposed control algorithm is effective and provides significant improvement in system performance. Therefore, the proposed PSO-PID controller is recommended to generate good quality and reliable electric energy. In addition, the proposed controller is very simple and easy to implement since it does not require many information about system parameters.
In this work, load damping coefficient D and load change ΔPL are taken as variables for variation of load parameters. The authors have taken the inertia constant H also as a variable for variable load parameter.
F=60Hz, R1=0.05, R2=0.0625, D1=0.6, D2=0.9, H1=5, H2=4, Tg1=0.2sec, Tg2=0.3sec, Tt1=0.5sec, Tt2=0.6sec, Base power = 1000 MVA.
Pop size = 10;
ωmax = 0.9
ωmin = 0.4
CR = 0.65
c1 = 2.0
c2 = 2.0
iter_max = 30