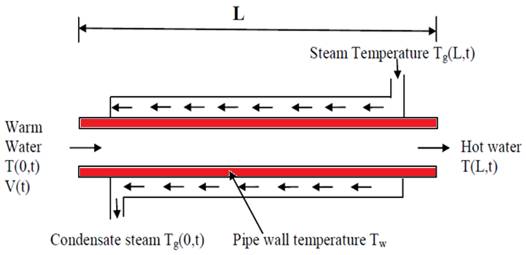
Figure 1. Schematic Diagram of Tubular Heat Exchanger
The main purpose of using controllers in heat exchanger is to control the fluid outlet temperature to its set point. Several controllers are in use to control the set point in a heat exchanger. In tubular heat exchangers, due to the flow induced vibration resonance occurs. If the vibration is high, it can cause damages to the tubes present inside the tubular heat exchanger. To eliminate this problem, repetitive controller is used which can easily cancel out the resonance dynamics present. In this paper, design of a tubular heat exchanger and Repetitive Controller is done and the simulation results are also provided.
Heat Exchangers are used widely in many industries. The main purpose of the heat exchanger is to transfer heat from a hot fluid to a cold fluid and vice versa. It is used to regulate the outlet fluid temperature to a particular set point. Basically there are two types of heat exchanger namely, Mixing type and Non mixing type. Mixing type can also be called as direct or contact type where there is no wall between the hot fluid and the cold fluid. On the other hand, non mixing type can also be called as indirect type where, the hot fluid and the cold fluid are separated by a metal wall.
Many controllers are used widely to control the outlet fluid temperature at its desired value [1, 7]. The outlet fluid temperature which is inside the pipe is controlled by varying the temperature of the outside fluid [2]. When this process variable is not available for control, the inside fluid velocity can be used for controlling the inner fluid temperature. Thus, the outlet fluid temperature can be controlled either by controlling the temperature of the fluid which is flowing outside or by controlling the velocity of the fluid which is flowing outside. But in both the cases, the resonance dynamics occur which will affect the outlet temperature. Hence, a controller is required which can eliminate these resonance dynamics.
Repetitive Control scheme is used to track the periodic references or to reject the periodic disturbances [5, 8]. Therefore, by proper design, the resonances that occur in the heat exchanger can also be eliminated with the help of this repetitive controller. The concept of this Repetitive controller is used widely in CD [10] and disk arm actuators, damper rigs [3], pulse width modulated inverters [11], speed control of ultrasonic motors[12], DC motors [13] etc.
The schematic diagram of the heat exchanger is shown in Figure 1. The heat exchanger shown in the figure is a counter flow tubular heat exchanger. Here, the warm fluid flows through the inner pipe at velocity ν(t) which can be varied with time. The inner fluid can be heated with the help of the saturated steam condensing on the outside of the inner pipe. The length of the pipe is of L meter. The assumptions made in the heat exchanger design are:

Figure 1. Schematic Diagram of Tubular Heat Exchanger
Mathematical modeling is a method of description of a system in mathematical language [4]. In mathematical model development for the heat exchanger, the following steps are performed.
1. The energy balance equation for the system has to be stated in differential form.
2. Parts of the function which are responsible for nonlinearity have to be identified.
3. The nonlinear part of the function has to be expanded as a first order Taylor series around a steady-state value.
4. Linearised function has to be reintroduced into the model and then simplified.
5. The model has to be expressed in terms of deviation variable and then be simplified.
6. Laplace Transform has to be applied.
7. Finally, the differential equation has to be solved and then has to be simplified.
The energy balance equation of the fluid inside the pipe over the volume element of length Δx can be written as

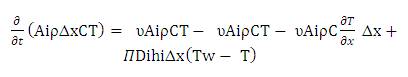
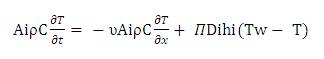
Divided by AiρC
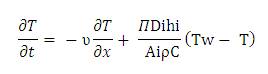
Let 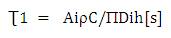
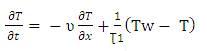
Here the term 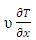 is non linear. Hence, the Taylor series expansion around the point ( υ=υs, T = Ts ) are used to obtain the linear approximation.
is non linear. Hence, the Taylor series expansion around the point ( υ=υs, T = Ts ) are used to obtain the linear approximation.
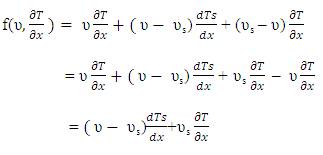
Substitute equation (5) in equation (4),
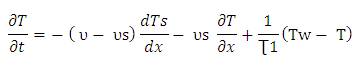
The energy balance equation over the volume element Δx is given by
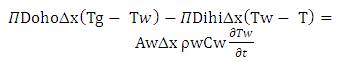

Dividing by AwρwCw

Let, 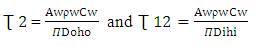
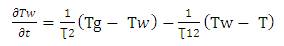
Equations (6) and (10) can be written in terms of deviation variables around steady-state conditions.

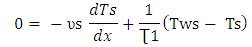
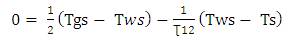
Steady state temperature is only a function of x, and it can be obtained by solving equations (12) and (14)
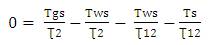
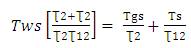
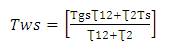
Substituting Tws in equation (12) we get
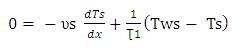
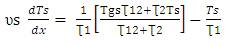
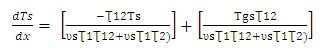
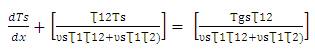
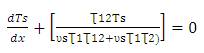
Let,

Solving for Ts ,

Where, Tso = Ts(X=0,t=0)
Subtracting equation (7) and equation (12) and introducing deviation variable,

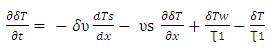
Subtracting equation (10) and equation (13) and introducing deviation variables,
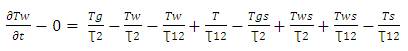
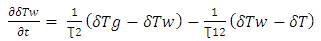
Where,
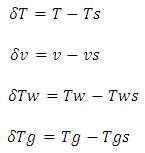
Taking Laplace transform for (24) and (26) and using the dependent variables  and
and 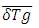 to represent the laplace transform of, δT, δυ, δTw , δTg respectively.
to represent the laplace transform of, δT, δυ, δTw , δTg respectively.

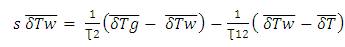
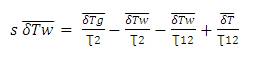
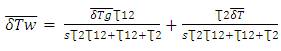
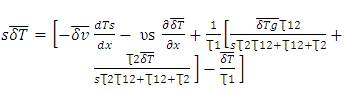
Substituting in equation (28),
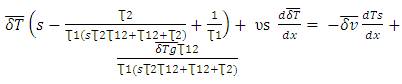
Let  and
and
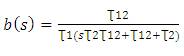

Divide by υs ,
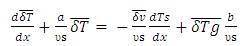
Solving equation (35) with boundary condition 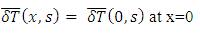 x at x =0 gives
x at x =0 gives
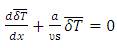
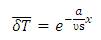
Equation (35) becomes
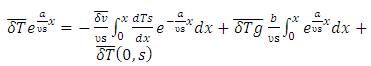
The dTs can be found from equation (23) as

Substituting equation (39) in (38),
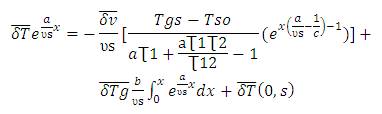
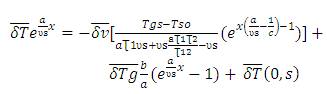
Dividing by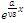

In equation (44), if the steam temperature and fluid velocity do not vary then the transfer function relating to the fluid outlet temperature and the incoming fluid temperature can be given by,
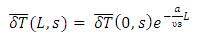
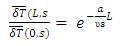
If the temperature and the velocity of the fluid entering the pipe do not vary, then the transfer function relating to exit fluid temperature and steam temperature can be written as,
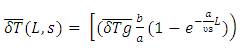
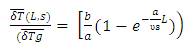
If the steam temperature and the incoming fluid temperature do not vary, then the transfer function relating to the fluid outlet temperature and flow can be written as
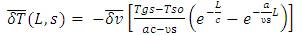
Substituting the value for a as,
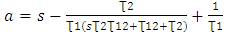 We get
We get
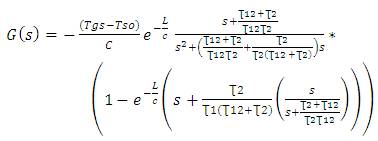
A heat exchanger is a heat transfer device that exchanges heat between two or more process fluids. Water is used as a fluid inside the pipe and steam is used to heat the cold o water. The temperature of the inlet fluid is 30oC and that for outlet fluid is 150oC. The mass flow rate of the fluid is 2kg/s. The inside diameter of the inner pipe is 4cm and the wall thickness is of 2mm. The material used for the pipe is made of copper.
Repetitive control is a linear control technique developed by a group of Japanese scholars in 1980s. It is based on internal model principle [9]. Repetitive Control is used to track the periodic references and to reject the periodic disturbances [5]. Repetitive Controllers are usually used as a 'plug in' type along with the normal conventional controllers [6]. The block diagram of the repetitive controller -N is shown in Figure 2. Here Z-N is a discrete time delay, F (Z) is a low pass FIR filter , L(Z) is the transfer function of the internal repetitive control loop, Gx(Z) is a linear filter for system X stability, Gc(Z) is the controller and Gp(Z) is the system to be controlled. F(Z) value can be taken as 1.
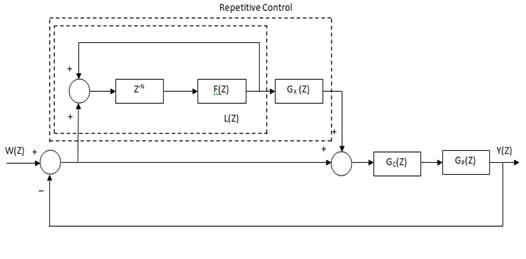
Figure 2. Repetitive Controller
To implement repetitive control, the transfer function G(s) relating fluid outlet temperature to fluid velocity has been used. The zero-order hold discretization method was employed for the implementation of the repetitive control scheme.
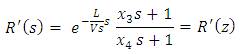
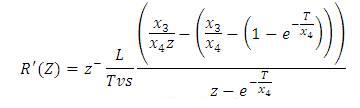

where T is the sample time used to discretize the continuous time models, 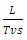 is rounded to the nearest integer, g = x3/x4,
is rounded to the nearest integer, g = x3/x4, 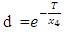 and f = g – (1-d). Using the repetitive control scheme and with F(z) = 1,
and f = g – (1-d). Using the repetitive control scheme and with F(z) = 1,
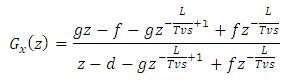
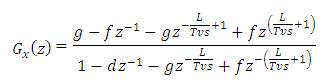
Therefore the transfer function of the internal repetitive control loop L(z) becomes,
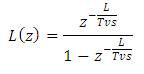
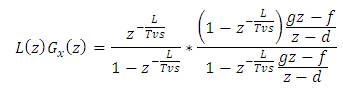
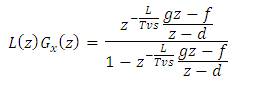

Equation (49) can be split into two terms. The second term R(S) is responsible for the resonance dynamics. This R(S) can be cancelled by multiplying it with a new transfer function C(S).
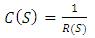
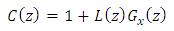
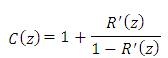
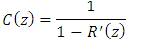
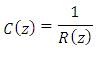
This way, the transfer function of the repetitive controller is the discrete form of the transfer function necessary to counteract the resonance dynamics.
The software used for the simulation is MATLAB - Simulink. An open loop step response test was done in order to analyze the system behavior. The higher order model of the heat exchanger is reduced into a first order system. Here, the fluid mass flow value was decreased from 2kg/s to 1.5334 kg/s. The open loop step response for tubular heat exchanger is shown in Figure 3. The frequency response of the heat exchanger is shown in Figure 4. The resonance effect present in the heat exchanger is due to the flow induced vibration. When the flow induced vibration exceeds certain amount, it can damage the tubes. Hence it is crucial to take care of these periodic oscillations. The Tubular heat exchanger is controlled using PI controller, IMC Controller and also PI + Repetitive Controller. The PI controller and IMC controller can be used to achieve the set point value. But, it cannot eliminate the resonances present in the system. On the other hand, the Repetitive controller can be used both to control the set point and also to eliminate the periodic disturbances. The bode plot of the heat exchanger system along with PI controller is shown in Figure 5. From the bode plot of the heat exchanger system along with PI+Repetitive Controller shown in Figure 6, it is evident that the resonance dynamics are eliminated. For this reason, the PI+Repetitive Controller is used to eliminate the periodic oscillations.
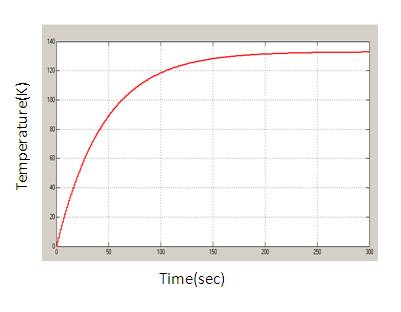
Figure 3. Open loop response of heat exchanger
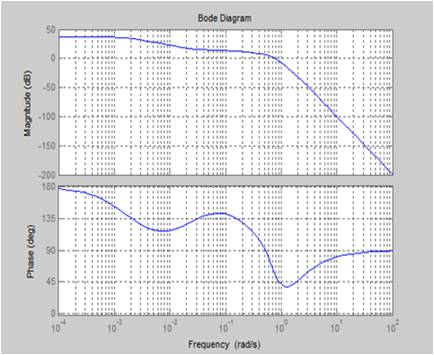
Figure 4. Frequency response of tubular heat exchanger
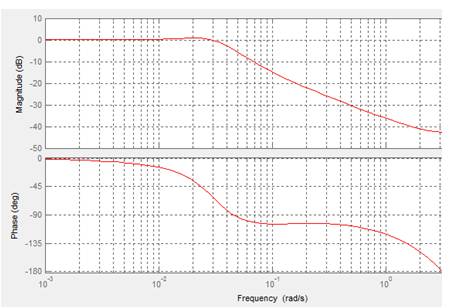
Figure 5. Frequency response of system with PI controller
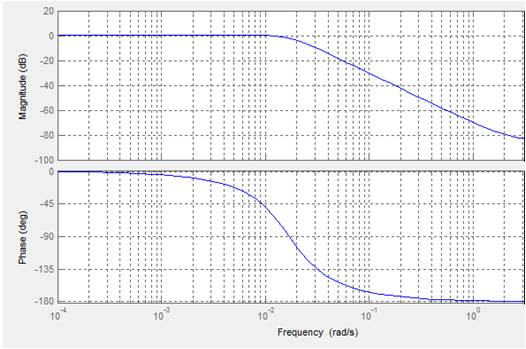
Figure 6. Frequency response of the system with PI+Repetitive controller
The time response for the system with PI controller is shown in Figure 7. From the Figure it is clear that the PI controller can be used to achieve the set point although its resonances and cannot be eliminated.
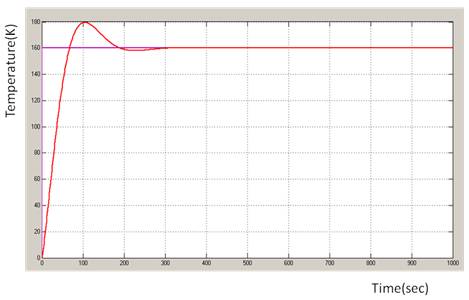
Figure 7. Response of heat exchanger system with PI controller
The time domain response of tubular heat exchanger system along with IMC controller is shown in Figure 8. From the figure, it is obvious that the IMC controller has better rise time and settling time compared with the conventional PI controller.
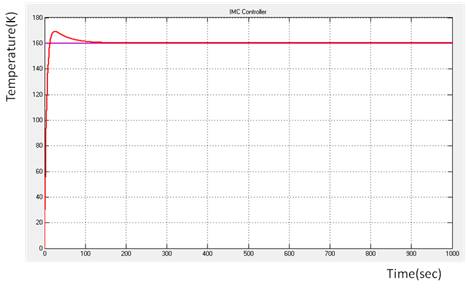
Figure 8. Response of the system with IMC controller
The response of heat exchanger system along with PI+Repetitive controller is shown in Figure 9. The frequency response of the system along with PI+Repetitive controller shown in Figure 6. shows that the resonance present in the heat exchanger system are completely eliminated. This shows that the Repetitive controller has the tendency to eliminate the periodic oscillations present in the system.
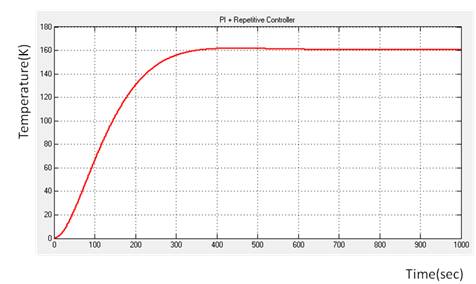
Figure 9. Response of the system with PI+Repetitive controller
Repetitive Control scheme has been proposed for improving fluid outlet temperature control in heat exchangers by taking resonance dynamics into account. With the help of Repetitive Controller, it is possible to achieve a well damped closed response which cannot be achieved with a simple PI Controller. Full resonance cancellation is easy to achieve in the simulation. However, in real plant operation, fast actuators are required to get better performance. The periodic oscillations produced by the flow induced vibrations are eliminated completely with the repetitive controller.