[1]
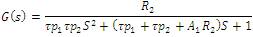
A multi tank level control system is an example of interacting systems. In this paper, the authors considered two first order systems connected in series, one rectangular tank which has inflow of liquid into the tank and out flow. The outflow of first tank is the inflow for second tank through a control valve. The control System is intended to maintain the level of liquid in the second tank at some predefined value irrespective of changes of inflow to the first tank. Fractional Order PID (FOPID) controller is a powerful controller used in process industries to regulate and control process variables. The errors of the process variables are minimized proportionally, integrally and derivatively. Fractional Order PID controller gives better results for changes in set point and disturbance rejections. The change in inflow or changes in predefined values are treated as disturbances to the process. According to these disturbances, they need to implement better tuning algorithms to Fractional Order PID controllers. In this paper, they implemented different Fractional Order PID control algorithms on a multi tank level control System and their responses are observed and also compared with Conventional PID controllers.
When a material or energy flows through a single capacity they get first order systems. If on the other hand, mass or energy flows through a series of two capacities, the behaviour of the system is described by second order dynamics [1]. In multi-capacity systems tank 1 feeds tank2 and it affects it's dynamic behaviour, whereas the opposite is not true. Such system has characters of a large class of non interacting capacities or non interacting first order systems in series. The overall transfer function of interacting systems is
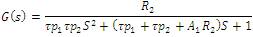
Where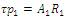 
and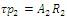 
are time constants of the two tanks.
It is generally believed that PID controllers are the most popular controllers used in process control [2]. Because of their remarkable effectiveness and simplicity of implementation, these controllers are overwhelmingly used in industrial applications, and more than 90% of existing control loops involve PID controllers [3]. Since the 1940s, many methods have been proposed for tuning these controllers, but every method has brought about some disadvantages or limitations [4-7]. As a result, the design of PID controllers still remains a challenge before researchers and engineers
A PID controller has the following transfer function:
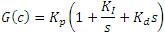
In Non-integer order controllers for integer order plants, there is better flexibility in adjusting the gain and phase characteristics than using IO controllers [8]. Fractional order PID controllers give better performance than their integer order counterparts. Controller synthesis is based on required peak overshoot and rise time specifications [9]. A PID controller calculates an error value as the difference between a measured process variable and a desired set point. The controller attempts to minimize the error by adjusting the process control inputs [10]. The main reason for using the integer-order models was the absence of solution methods for fractional differential equations [11]. To design FOPID controller is to determine two important parameters λ (integrator order) and μ (derivative order).In this paper, it is shown that the response and performance of FOPID controller is much better than integer order PID controller for the same system [12] . The performance of a PID controller deteriorates when implemented with lossy capacitors in its analog realization [13]. The parameters of the PIλDμ controller are Found and injected to the controller structure. The main specification of this method is that all five parameters of PIλDμ controller have been found directly without spreading the steps of computation [14]. Better performance using fractional order PID controllers can be achieved and is demonstrated through two examples with a comparison to the classical integer order PID controllers for controlling fractional order systems [15].
A PID controller has the following transfer function:
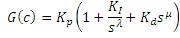
Tuning of PID controller is selection of Kp , Ki and Kd values. This selection process was carried by open loop process which means, without controller they applied step input to process and its behaviour was observed as showing in Figure1. The graph calculations are L=2s, T=29.6s, K=1. for simulation, we have considered the multi tank parameters which are
R2 =1(steady state gain of tanks);
τ ρ1 =10(Time constant of Tank1 system)
τ ρ2 =10(Time constant of Tank2 system)
A1 R2 =30 (The interacting factor of two tanks)
µ = 0.5;
λ = 0.5;
Figure 1. Open loop response
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figures 2 - 7 and the Time domain specification of the above non interacting system under various tuning algorithms are tabulated in Table 1.
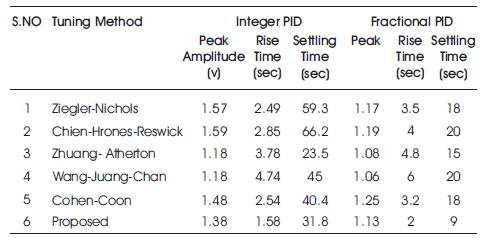
Table 1. Comparison of Integer PID and Fractional PID
According to Ziegler-Nicholas the tuning parameters are
The controller parameters are
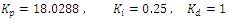
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figure 2.
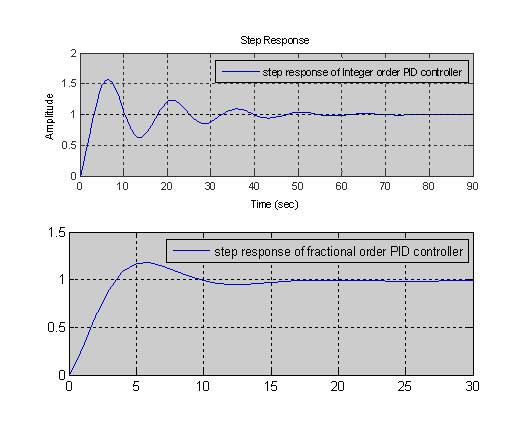
Figure 2. Ziegler-nichols response
According to Chien-Hrones-Reswick, the tuning parameters are
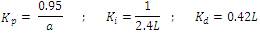
Then the controller parameters are
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figure 3.
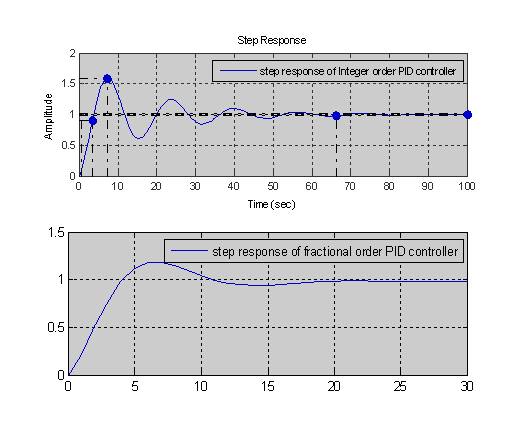
Figure 3. Chein-Hrones-Reswick response
According to Cohen-Coon algorithm, tuning parameters are
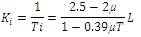
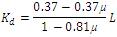
The controller parameters are
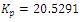
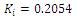
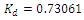
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figure 4.
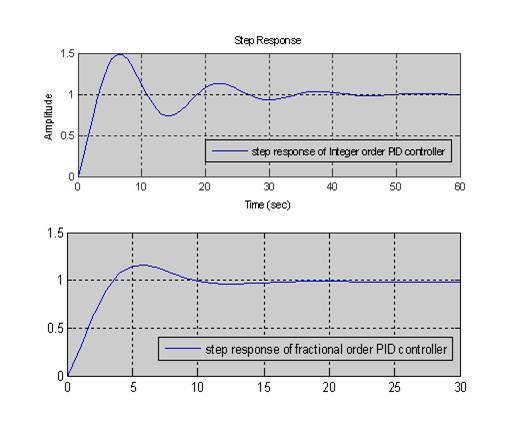
Figure 4. Cohen-Coon response
Based on the optimum ITAE criterion, the tuning algorithm proposed by Wang, Juang, and Chan is a simple and efficient method for selecting the PID parameters. If the K, L, T parameters of the plant model is known, the controller parameters are given by
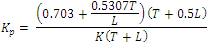
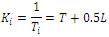
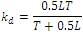
The controller parameters are
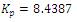
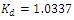
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figure 5.
Figure 5. The Wang–Juang–Chan response
Optimum setting algorithms for a PID controller were proposed by Zhuang and Atherton for various criteria. Consider the general form of the optimum criterion
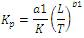
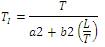
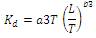
Where a1= 1.048; a2=1.195; a3= 0.489 b1= −0.897; b2= −0.368; b3=0.888
The controller parameters are
The step response of the multi capacity tank system for the above tuning algorithms is shown in Figure 6.
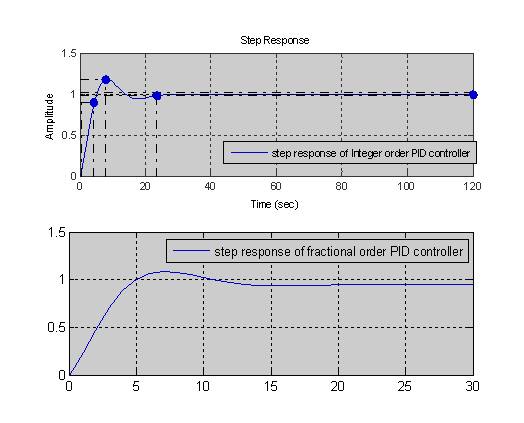
Figure 6. Optimum-PID response
The proposed tuning is a combination of Ziegler-Nichols and Chien-Hrones-Reswick tuning methods which produce better results compared to Ziegler-Nichols tuning method which are noted in Table 1 and its response is shown in Figure 7.
Figure 7. Proposed-PID response
The study of Fractional Order PID Controllers is an emerging field to get a mere understanding of the implementation of control techniques. In this paper, the authors have studied and showed the simulation step response results of multi capacity tank level control system for different Fractional Order PID algorithms. The Zhuang-Atherton algorithm shows best time domain specifications compared to remaining algorithms. Optimum tuning algorithm provides minimum settling time among other methods and the proposed tuning gives better tuning specifications compared to Ziegler-Nichols as shown in Table1