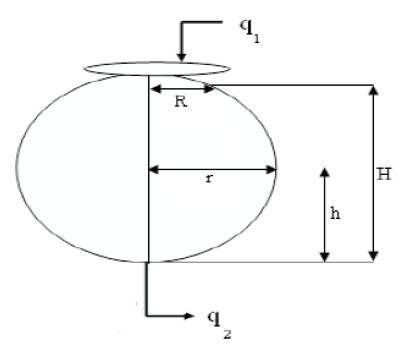
Figure 1. Schematic Diagram of spherical tank system
Fractional Order PI Controller Technique (FOPIC) offers success due to emerging of effective methods in differentiation and integration of the no integer order equation. In this research, the controller design using FOPIC is determined for a nonlinear system. The nonlinear system is taken up for the study is a spherical tank which is approximated to a first order system. Simulation is made by the MATLAB software.
The control of liquid level in tanks is a basic problem in process industries. The nonlinear system exhibits many challenging control problems due to their nonlinearity dynamic behavior and time varying parameter. The spherical tank exhibits nonlinearity due to its shape. Nithya et al. (2008) [2] proposed that the designing a controller for a nonlinear system is complex and difficult to implement. The main task of the controller design is to achieve the desired operating conditions and design the controller to achieve its optimum performance.
V.R.Ravi et al. [1] proposed about the need to control a Level because if the level is too high, that may upset reaction equilibria and cause damage to process equipment, which result in spillage of valuable or hazardous material. If the level is too low, that may have bad consequences for the sequential operations. Therefore, control of liquid level is an important and common task in process industries. Nonlinear models are used where accuracy over a wider range of operation is required and where they can be directly incorporated into control algorithms. Because of the inherent nonlinearity, most of the chemical process industries are in need of traditional control techniques. Anandanatarajan.R et al. [3]have done work in the evaluation of the controller using a variable transformation on a hemispherical tank. S.Nithya et al [4] propose that the nonlinearity of a spherical tank system by using system identification using black box model is approximated to a first order plus dead time model. The controller tuning has been applied using Skogestad's PI tuning technique and compared to the soft computing technique such as genetic algorithm. They discussed the control aspects using Internal Model controller PI tuning settings which give better performance in tracking the set point ad load changes. [8]
In Control engineering, conventional controllers are widely used in industries since they are simple, robust and familiar to the field operator .The Proportional Integral (PI) controllers are widely used in industries for process control applications to control the level of the liquid in a tank. The merit of using PI controllers lies in its simplicity of design and good performance including low percentage overshoot and small settling time for slow industrial processes.
J.G.Ziegler et al propose that the Ziegler-Nichols ultimate cycle tuning is the most popular method to tune the parameter settings of conventional controllers This is because the PID controller structure is simple and its principle is easier to understand than most other advanced controllers. Proportional control is designed to eliminate the cycling above and below the set point associated with the on-off control. Proportional response is the most common effect found in all controllers. The measure of the proportional response is called sensitivity. Sensitivity adjustment is necessary if optimum control stability is to be attained. It is common knowledge that control with the infinitely high proportional response is always unstable, oscillating continuously.
Automatic reset response is only purpose is to eliminate offset. It corrects for any offset automatically over time by shifting the proportional band. Reset redefines the output requirements at the set point until the process variable and the set point is equal. The reset time constant must be greater than the process response. If the reset value is too small, a continuous oscillation will result. If the reset value is too long, the process will take too long to settle out at the setpoint.
Proportional Integral Derivative (PID) processes with long time lags and large maximum rate of rise require wide proportional bands to eliminate oscillation. The wide band can result in large offset by changes in load. To eliminate these offsets, automatic reset can be used. Derivate action can be used in processes with long time delays to speed recovery after a process disturbance. It provides the most accurate and stable control of the three controller types and is best used in ones which have a relatively small mass and those which react quickly to changes in energy added to the process.
Subhransu Padhee et al [6] and Arijit Biswas et al. [13] have done work on FOPIDC where the integral and derivative actions orders are usually fract ional. Chunna Zhao et al. [10] propose that, besides setting the proportional, Integral and derivative constants Kp ,Ti and Td respectively, there are two more parameters λ, μ the integral and derivative orders respectively. Igor.p [14] proposes that, if λ=1 and μ=1, then it becomes an integer PID. If λ, μ are in fract ions, then it becomes fractional order PID. This is because the PID controller structure is simple and its principle is easier to understand than most other advanced controllers. [5]
In this paper, the main research is based on a FOC method for PI controller and it is said that it provides a better controller when compared to that of the conventional controller.
The paper is organized as follows: In section 1, the mathematical modeling of the conical tank system to determine the transfer function is described. In section 2, the controller techniques for FOC was designed for PI controller. In section 3, finally the results and conclusion are discussed.
The mathematical model of the Spherical tank shown in Figure 1 is determined by considering two assumptions (i) level as the control variable (ii) inflow to the tank as the manipulated variable [6]. This is achieved by controlling the input flow into the tank.

Figure 1. Schematic Diagram of spherical tank system
Operating Parameters are
q1 - Inflow rate of the tank
q2 - Outflow rate of the tank
H - Total height of the spherical tank.
R - Top radius of the spherical tank
h - height of the spherical tank at radius R
r - Radius of the spherical tank
Mass balance Equation is given by [7]
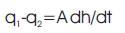
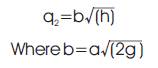
Where a- area of the tank at the outlet
g- acceleration due to gravity
Transfer function is given by taking the partial differentiation of the linearised equation and its corresponding Laplace transforms,

where τ = KA
K= 2 √(h)/b
Specifications
H - Total height of the conical tank =60cm
R - Top radius of the conical tank =5cm
a- area of the tank at the outlet =0.8cm
Based on the specification, the transfer function is given by, G(S)=1.76/(19903.84S+1)
The concept of FOPIDC was proposed by Podlubny in 1997 was given by Y.Q.Chen et al. [17] and also demonstrated the better response of this type of controller, in comparison with the classical PID controller, when used for the control of fractional order systems. Monje in 2004 an optimization method is presented where the parameters of the FOPIC are tuned such that predefined design specifications are satisfied.
The differintegral operator, denoted by aDqt , is a combined differentiation-integration operator commonly used in fractional calculus and was proposed by C.Priya et al. [7]. This operator is a notation for taking both the fractional derivative and the fractional integral in a single expression and is defined by Mohammad et.al as [11]
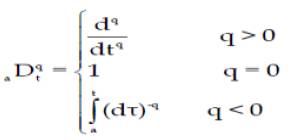
Where q is the fractional order which can be a complex number and a and t are the limits of the operation. There are some definitions for fractional derivatives. The commonly used definitions are Grunwald–Letnikov, Riemann– Liouville, and Caputo definitions and it was proposed by yun-li cao et al. [16].
The most common form of a Fractional Order PID Controller is the PIλDμ controller, involving an integrator of order λ and a differentiator of order μ, where λ and μ can be any real numbers as proposed by Vaithiyanathan et.al. [15]. The transfer function of such a controller has the form,
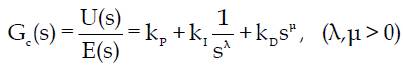
where Gc(s) is the transfer function of the controller, E(s) is an error, and U(s) is controller's output. The integrator term is 1 s λ, that is to say, on a semi-logarithmic plane, there is a line having slope -20λ dB/decade. The control signal u(t) can then be expressed in the time domain as
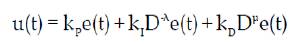
Deepyaman Maiti et al. [9] propose that selecting λ = 1 and μ = 1, a classical PID controller can be recovered.The block diagram shown in Figure 2 represents the selections of λ = 1, μ = 0, and λ = 0, μ = 1 respectively which corresponds to conventional PI & PD controllers.
Figure 2. The Block diagram of Expanding value of FOPIDC
All these classical types of PI controllers are the special cases of the fractional PIλ controller. It can be expected that the PIλ controller may enhance the systems control performance and its block diagram is shown in Figure 3. One of the most important advantages of the PIλ controller was proposed by Bijoy K.Mukherjee etal. [12] that it provides the better control of dynamical systems, which are described by fractional order mathematical models. Another advantage lies in the fact that the PIλ controllers are less sensitive to changes of parameters of a controlled system. This is due to the two extra degrees of freedom to better adjust the dynamical properties of a fractional order control system.
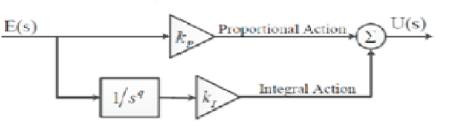
Figure 3. The Block diagram of FOPIC
Let us consider a process defined by FOPDT model is given by
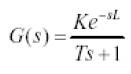
The process dynamics can be conveniently characterized by the normalised dead time and its response curve is shown in Figure 4 and it is defined as
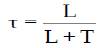
The following control parameters based on the model by Y.Q.Chen et al. [18].
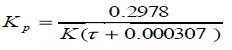
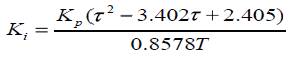
Kp=0.6759
Ki=0.0004247
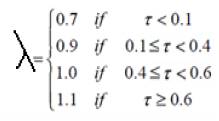
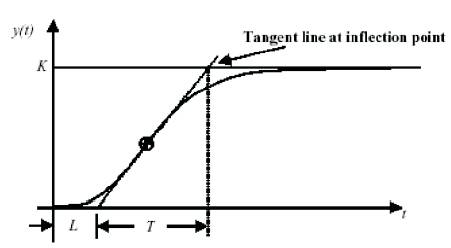
Figure 4. The response curve for the first order system
Simulation results obtained for the closed loop system is given below. Figure 5 shows the output for a closed loop system having a set point of 30cm which is 50% of its nominal value. Figures 6, 7 and 8 show the results of the servo response of the process having a step change which provides a faster controller output change. Figures 9 and 10 provide the regulatory response change by giving a load disturbance to the system. Figure 11 describes the servo and regulatory change of the nonlinear spherical tank system.
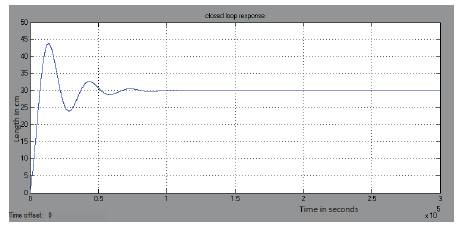
Figure 5. Closed Loop response of FOPI system of setpoint 30cm
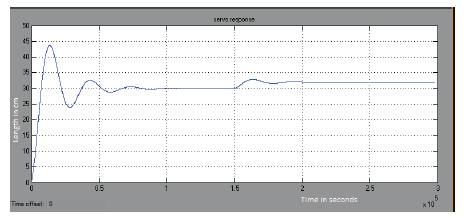
Figure 6. Servo response of Closed Loop FOPI system of changein setpoint from 30cm to 32cm
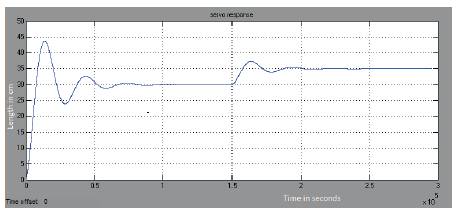
Figure 7. Servo response of Closed Loop FOPI system ofchange in setpoint from 30cm to 35cm
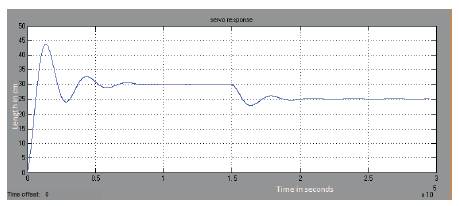
Figure 8.Servo response of Closed Loop FOPI system of change in setpoint from 30cm to 25cm
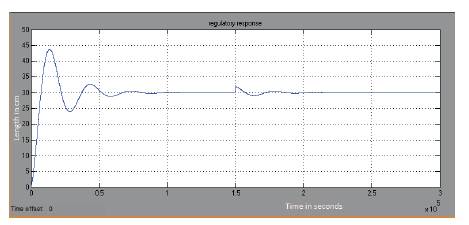
Figure 9.Load Disturbance of Closed Loop FOPI system at setpoint 30cm

Figure 10.Load Disturbance of Closed Loop FOPI systemat setpoint 30cm
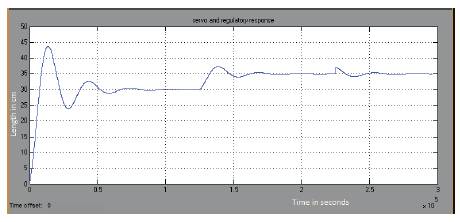
Figure 11.Servo and Regulatory response of Closed Loop FOPI system at setpoint 30cm
Simulation is performed by using MATLAB for the FOPI Controller to validate the performance of the spherical tank system. It is analyzed that the FOPI controller provides a better output with less settling time. The simulation is carried out by taking 50% as the nominal value by taking λ=0.7.