
The present paper studies the effect of aligned magnetic field on an unsteady MHD free convection Casson fluid flow past an infinite plate through porous medium in the presence of thermal radiation and heat absorption. When t*>0, the velocity u*=u0, and that time, plate temperature and the concentration are raised to T*w and C*w and a first order chemical reaction takes place. A uniform magnetic field B0 is applied in y*-direction. The systems of non-dimensional governing linear partial differential equations are solved analytically by using the Laplace transform technique. The influences of various non-dimensional parameters on the velocity, the temperature, the concentration, the Sherwood numbers, the local Nusselt and the skin friction have been discussed and analyzed through graphs and tables.
The study of non-Newtonian Casson fluid can be defined as a shear thinning liquid which is assumed to have infinite viscosity at zero rate of shear, a yield stress below which no flows occurs. If a shear stress less than the yield stress is applied to the fluid, it behaves like a solid, where as if a shear stress greater than yield stress is applied and it starts to move. Few examples of Casson fluids are jelly, tomato sauce, honey, concentrated fruit juice, blood etc. Casson model is sometimes stated to fit rheological data better than general viscoelastic model for many materials. Many authors have their research in Casson fluid for mathematical modeling. Ostrach, (1952) has analyzed free-convection flow and heat transfer of a fluid flow over a flat surface parallel to the direction of the generating body force. Chemical reaction, heat absorption and Hall effect on magneto hydro dynamics (MHD) convective in vertical porous plate were investigated by Masthanrao, Balamurugan, Varma, and Raju, (2013). McGregor, (1970) has done research on the application of the minimal energy hypothesis to a Casson Fluid. Kirubhashankar, and Ganesh, (2014) examined chemical action effect on MHD flow of a Casson fluid within the present of heat transfer and mass transfer. The impact of mass transfer on MHD flow of Casson fluid with chemical reaction was studied by Shehzad, Hayat, Qasim, and Asghar, (2013). The influence of Newtonian heating on steady hydro magnetic Casson fluid flow with heat and mass transfer was analyzed by Das, Mahato, and Nandkeolyar, (2015). Kumar, Varma, and Mohan, (2012) found heat transfer, mass transfer, chemical revulsion and radiation expansion on magneto hydro dynamics convection proceed in vertical plate. Heat transfer and mass transfer in MHD flow of a Casson fluid with convective boundary conditions was analyzed by Pushpalatha, Sugunamma, Reddy, and Sandeep, (2016). Raju, Reddy, and Reddy, (2016) thought of chemical reaction and radiation absorption effects on magnetohydrodynamic Casson fluid flow past periodical vertical porous plate.
Sakiadis, (1961) analyzed the boundary layer flow over a continuous solid surface. Diffusion of with chemicals reactives species in Casson fluid stream over an unsteady passable tensive exterior was analyzed by Mukhopadhyay, and Vajravelu, (2013). Free convection flow past an accelerated infinite plate was studied by Pop, and Soundalgekar, (1980). Newtonian heating and heat transfer effects on Casson fluid flow of an unsteady periodic plate was discussed by Hussanan, Salleh, Tahar, and Khan, (2014). Raptis, Singh, and Rai, (1987) discussed unsteady free convective flow through a porous medium near to a semi-limitless vertical plate worn limited variation outline. Arthur, Seini, and Bortteir, (2015) considered chemical process result on Casson fluid flow over a vertical porous surface among the presence of force field. Dash, Jayaraman, and Mehta, (2000) analyzed unsteady dispersion of a solute in a Casson fluid flowing in a pipe. Waqas, Rafique, Khalid, Hussain, and Ahamad, (2017) considered the influence of radiation on MHD slip flow and heat transfer of Casson fluids due to shrinking sheet immersed in porous medium. Reddy, (2015) studied unsteady radiative convective boundary layer flow of a Casson fluid with variable thermal conductivity. Viscous dissipation and heat source effects on free convective boundary layer slip flow in the presence of induced magnetic field were discussed by Balakrishna, Reddy, Mohan, and Varma, (2017). Effects of chemical reaction on unsteady MHD Casson fluid flow past a moving infinite inclined plate through porous medium was discussed by Balakrishna, Mohan, Reddy, and Varma, (2018). Effects of induced magnetic fields on free convection viscous dissipative fluid flow past a moving an infinite inclined plate in the presence of heat source was identified by Mohan, Bhaskarudu. Reddy, and Thajoddin, (2017a). The influences radiation and chemical reaction on conducting Newtonian and non- Netonian fluids from surfaces through porous medium has been studied by Mohan et al. [Mohan, Reddy, and Varma, (2019a), (2019b), (2019c), Mohan, Reddy, & Balakrishna, (2018), Mohan, Reddy, Varma, & Krishna, (2017b), (2017c), (2017d)]. Prakash, Kumar, Bhanumathi, and Varma, (2012) considered Dufour effects on unsteady hydro magnetic radiative fluid stream by a perpendicular diagram through porous ordinary. Vijaya Kumar, Veeresh, Varma, Umamaheswar, and Raju, (2017) analyzed MHD radiative and convective Casson fluid flow of a periodic vertical plate among the presence of Joule heating and thermal diffusion. Vijayaragavan, (2018) considered variable magnetic field effect of heat and mass transfer in radiative Casson fluid flow a vertical plate.
In the present study, we tend to analyze the consequences of thermal radiation, chemical reaction, aligned magnetic field and heat absorption on flow of Casson fluid past an infinite plate among the porous medium. The set of linear partial differential equations are solved analytically by using Laplace Transform technique. The effects of assorted non-dimensional quantities on velocity, temperature, concentration, Skin friction coefficient, Nusselt and Sherwood numbers are completely investigated by graphs and tables.
In this paper, the consideration is on the unsteady MHD free convection heat transfer and mass transfer flow of a viscous, incompressible, electrically, conducting, chemically reacting and radiating fluid past an infinite vertical plate in the presence of aligned magnetic field B0 which is applied an angle a to the fluid flow. Let X*-axis is taken on the plate and y* -axis is taken normal to it. Initially, when t*£0 each the fluid and plate are at stationary condition having constant temperature and concentration. When t*>0 then the velocity u*=u0. At an equivalent time, the plate temperature and concentration are raised to T*w and Cw*. For free convection flow, it is additionally assumed that, the evoked magnetic flux is negligible because the magnetic Reynolds range of the flow is taken to be negligible. The viscous dissipation is not taken within the heat equation. The effects of variation in density (ρ) with temperature and species concentration area unit thought of solely on the body force term, in accordance with usual Boussinesq approximation. The fluid thought of here is grey, absorbing/emitting radiation however a nonscattering medium. Since the flow of the fluid is assumed to be within the direction of x*-axis, that the physical quantities area unit functions of the area co-ordinate y*and t*only. The rheological equation of state for an isotropic and incompressible flow of a Casson fluid is given by Ullah, Khan, and Shafie (2016).
The following governing equations are:
Momentum equation

Energy equation
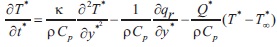
Concentration equation
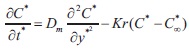
The initial boundary conditions are
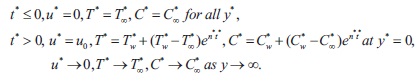
The radiative heat flux qr, under Rosseland approximation of the form
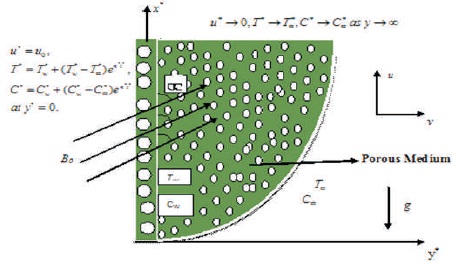
Figure 1. Physical Model
Where σ*-The Stefan-Boltzmann constant, k* - The mean absorption coefficient and The linear temperature operate T*4 is expanded by victimization Taylor series enlargement regarding T∞* as
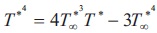
From the equations (5) and (6), the equation (2) reduces to
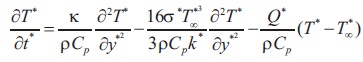
The following non- dimensional quantities are
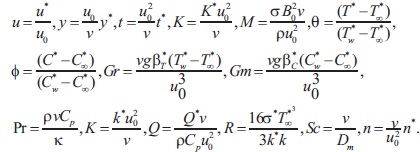
considering equation (8), the equations (1), (3) and (7), reduce to the following non-dimensional forms

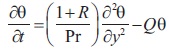
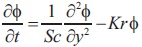
The corresponding boundary conditions reduce to
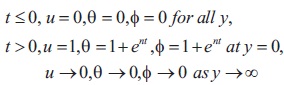
The system of equations (9), (10) and (11) with subject to the boundary conditions (12), are solved analytically by using Laplace Transform technique and the expression for
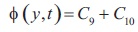

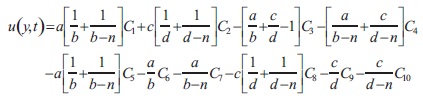

Sherwood number at y=0 is given by
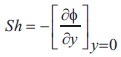
From the equations (13) and (16), the obtained Sherwood number is as follows
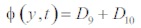
Nusselt number at y=0 is given by
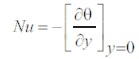
From equations (14) and (17), the obtained Nusselt number is as follows
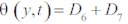
Coefficient of the Skin-friction at y=0 is given by
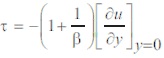
From equations (15) and (18), the obtained Skin friction coefficient is as follows
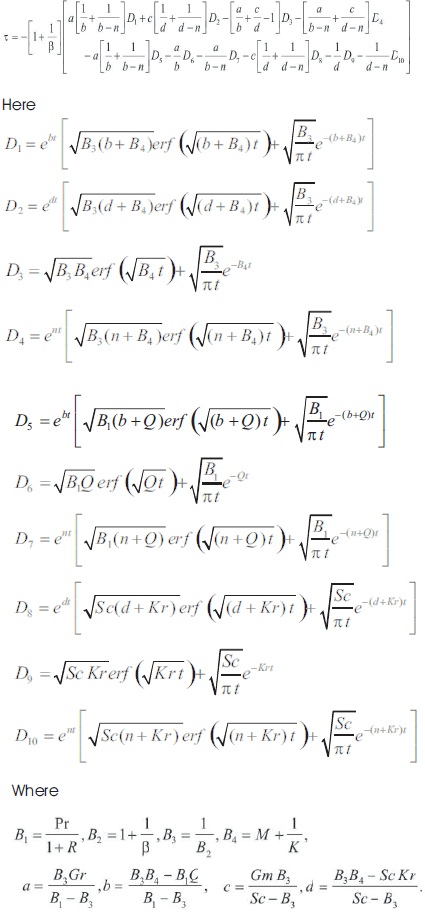
The systems of linear, non-dimensional equations (9) to (11), with boundary conditions (12), are solved analytically by using the Laplace Transform technique. The obtained solution reveals that the flow, heat and mass transfer of the fluid will be affected by various non-dimensional governing parameters, such as Casson parameter (b), aligned angle (α), Magnetic parameter (M), Prandtl number (Pr), Porosity parameter (K), heat absorption parameter (Q), thermal Grashof number (Gr), mass Grashof number (Gm), Schmidt number (Sc), chemical reaction parameter (Kr), thermal Radiation parameter (R) and unsteady parameter (t). The results for various nondimensional parameters on velocity, temperature, and concentration, skin friction coefficient and Nusselt and Sherwood number are displayed and discussed through graph and tables. Figures 2 to 19 are drawn to discuss the case of cooling (Gr>0, Gm>0) and heating (Gr<0, Gm<0) of the plate. The heating and cooling takes place by fixing free convection currents because of temperature and concentration gradient.
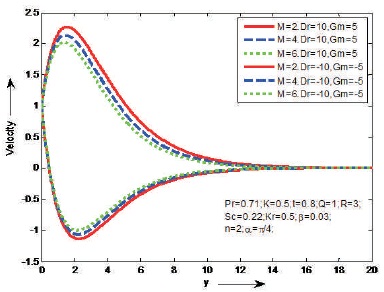
Figure 2. The Effect of M on Velocity
The influences of Magnetic parameter (M) and Prandtl number (Pr) on the fluid velocity are shown Figures 2 and 3, in case of cooling and heating of the plate. It is observed that the velocity decreases as M or Pr increases in case of cooling of the plate and opposite result is identified in case of heating of the plate. Figure 4 shows the effect of porosity parameter (K) on velocity in case of cooling and heating of the plate. It is found that the velocity will increase as K increases just in case of cooling of the plate. However, a reverse result is known just in case of heating of plate. Figure 5, reveal that the behaviour of α on velocity in case of cooling and heating of the plate. It is clear that the velocity increases as aligned angle (α) increases both cooling and heating of the plate. When α=π/2 we get the velocity flow in y-direction. Figures 6 and 7 depict the effects of thermal Grashof number (Gr), mass Grashof number (Gm) and heat absorption parameter (Q) on velocity in cases cooling and heating of the plate. From this it is observed that the velocity increases as Gr, Gm or Q increases in case of cooling of the plate and opposite result is identified in case of heating of the plate. The effect of thermal radiation (R) on velocity is shown Figure 8, in cases of cooling and heating of the plate. It is found that the velocity increase as R increases in case of of cooling of the plate. But reverse impact is known just in case of heating of plate. Figures 9 and 10, exhibit the effects of Schmidt number (Sc) and chemical reaction (Kr) on velocity in cases of cooling and heating of the plate. It is found that the velocity increases as Sc or Kr increases in case of cooling of the plate. But reverse impact is known just in case of heating of plate. The effect of Casson parameter (β) on velocity is shown in Figure 11, in case of cooling and heating of the plate. It is observed that the velocity increases initially and slowly decreases as β increases in case of cooling of the plate and opposite result is identified in case of heating of the plate. The influence of unsteady parameter (t) on velocity is shown in Figure 12, in case cooling and heating of the plate. It is seen that the velocity increases as unsteady parameter (t) increases in case of cooling of the plate. But reverse impact is known just in case of heating of plate.
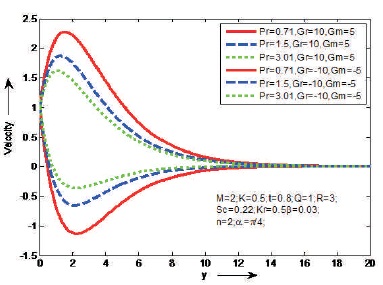
Figure 3. The Effect of Pr on Velocity
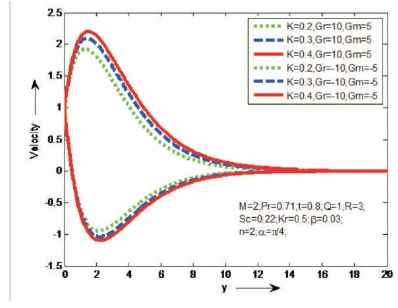
Figure 4. The Effect of K on Velocity
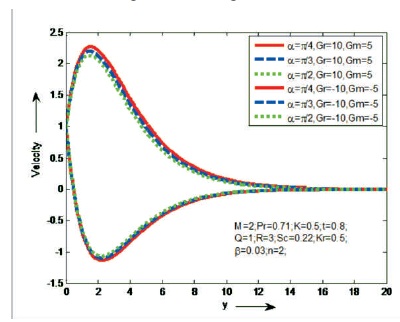
Figure 5. The Effect of α on Velocity

Figure 6. The Effect of Gr or Gm on Velocity
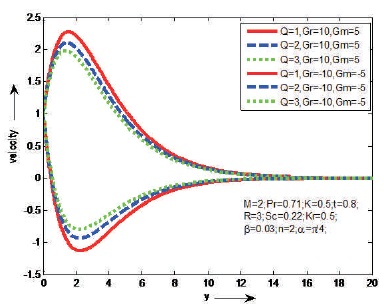
Figure 7. The Effect of Q on Velocity
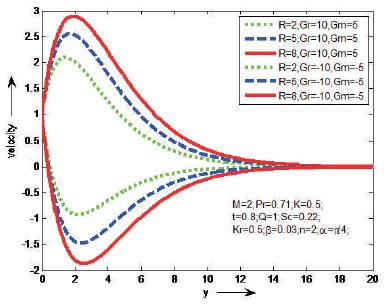
Figure 8. The Effect of R on Velocity
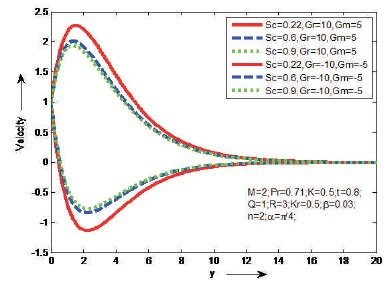
Figure 9. The Effect of Sc on Velocity
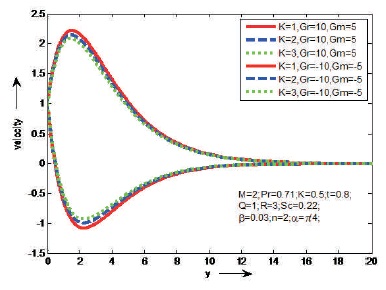
Figure 10. The Effect of Kr on Velocity
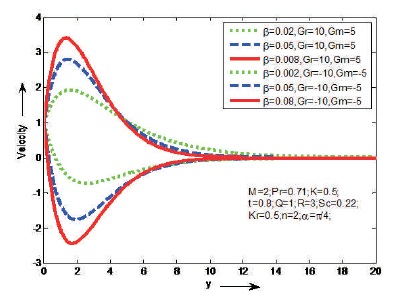
Figure 11. The Effect of β on Velocity
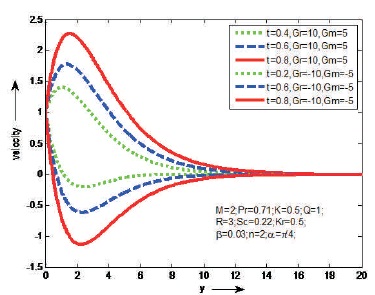
Figure 12. The Effect of t on Velocity
Figures 13 to 16 represents the effect of different flow parameters on the fluid temperature. Prandtl number (Pr) is outlined because the ratio of kinematic viscosity to thermal diffusivity. The influences of the Prandtl number (Pr) and the heat source parameter (Q) on the temperature are shown Figures 13 and 14. It is found that the temperature decreases as Pr or Q will increase on the fluid flow. From Figure 15, exhibit the effect of thermal radiation (R) on temperature. It is seen that temperature increases as R increases on the fluid flow. The influence of unsteady parameter (t) on temperature is shown in Figure 16. It is clear that the temperature increases as t increases on the fluid flow.

Figure 13. The Effect of Pr on Temperature
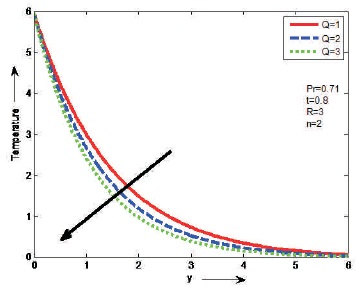
Figure 14. The Effect of Q on Temperature
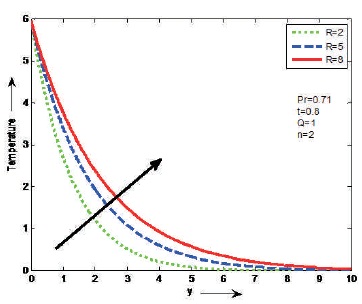
Figure 15. The Effect of R on Temperature
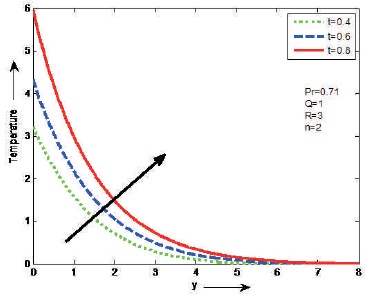
Figure 16. The Effect of t on Temperature
The effects of Schmidt number (Sc) and chemical reaction (Kr) on concentration are shown in Figures 17 and 18. It is noticed that the concentration decreases as Sc or Kr increases on the fluid flow. From Figure 19, depict the effect of unsteady parameter (t) on concentration. It is observed that the concentration increases as t increases on the fluid flow.
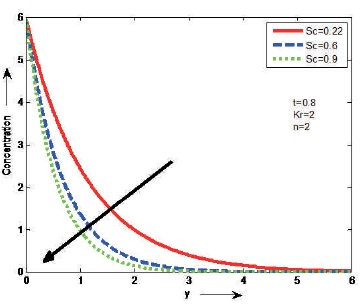
Figure 17. The Effect of Sc on Concentration
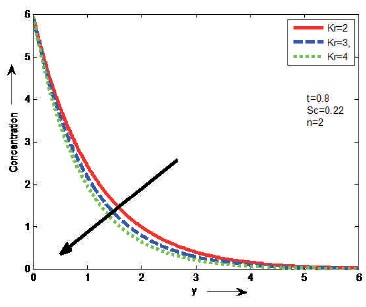
Figure 18. The Effect of Kr on Concentration
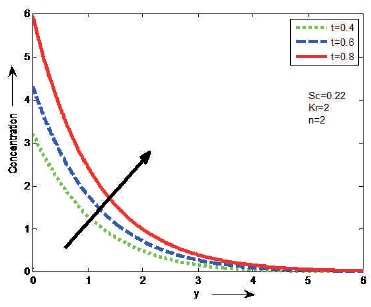
Figure 19. The Effect of t on Concentration
Table 1 depicts the behavior of Sherwood numbers. Sherwood number increases as the values of Sc or Kr increases and it decreases as t increases. Table 2, exhibits the influence of Nusselt numbers. Nusselt number increases as the values of Pr or Q increases and it reduces as the values of R or t increases. Table 3 shows that the effect of Skin friction coefficient in case cooling and heating. From this it is clear that the Skin friction coefficient increases as the values of Pr, Q, Sc, or Kr increases and it decreases as the values of R, t or β increases in case of cooling. But it has reverse effect in case of heating. In case of both cooling and heating, Skin friction coefficient in friction increases as the values of M or α increases and Skin friction coefficient decreases as the values of K increases.
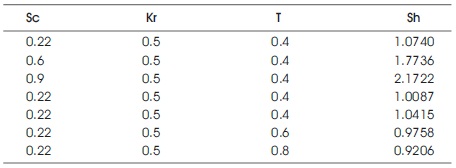
Table 1. Sherwood Number
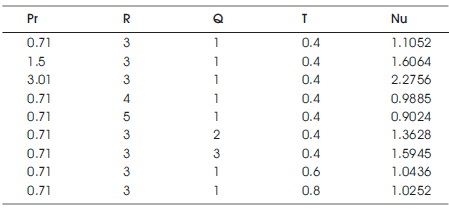
Table 2. Nusselt Number

Table 3. Skin Friction Coefficient; (for cooling Gr>0, Gm>0, for heating Gr<0,Gm<0)
From the current work the following conclusions are made:
Velocity increases with the values of K, Gr, Gm, R or t increases in case of cooling and reverse phenomenon is observed in case of heating. Velocity decreases with the values of M, Pr, Q, β, Sc or Kr increases in case of cooling and it is noticed opposite behaviour in case of heating. But both the cases the velocity increases with an aligned angle (α) increases. Velocity increases initially and slowly downwards as β increases in case of cooling and it has reverse effect in case of heating.
Skin friction coefficient increases as the values of Pr, Q, Sc, or Kr increases and it decreases as R, t or β increases. But the reverse effect is noticed in case of heating. In case of both cooling and heating, Skin friction coefficient increases as the values of M or α increases and the Skin friction decreases as the values of K increases.