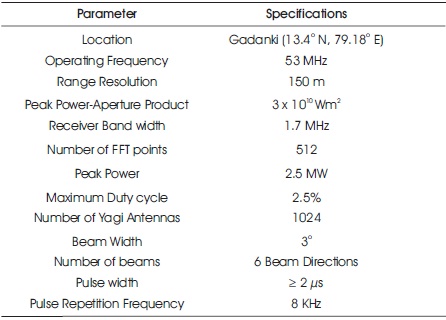
Table 1. Main Specifications of the Indian MST Radar
The Indian MST radar is sited at National Atmospheric Research Laboratory (NARL), Gadanki, Andhra Pradesh. The MST radar is used to study and characterize the dynamic changes of atmosphere in the regions of Mesosphere, Stratosphere, and Troposphere (MST). MST radar was developed with an active phased antenna array consisting of 1024 Yagi-Uda antenna elements and operated by a frequency of 53 MHz. In this article, a sparse iterative parameter estimation approach for spectral estimation for the radar data has been introduced. Separable models occur normally in spectral analysis, like radar signal processing and astronomy applications. The proposed algorithm for the simulated complex signal which may contain more than one frequency component in presence of noise has been tested. For simulated signal, the algorithm has proven to estimate the power spectrum at low SNR conditions also. Finaly, the proposed algorithm (PALG) has been applied to MST radar data collected on 9 Feb, 2015 to compute Doppler spectrum. After computing Doppler spectrum and Doppler velocities, the wind parameters like Zonal U, Meridional V, and Wind velocity can be calculated from the Doppler velocities. The obtained wind velocity components of the MST radar data is validated through the Global Positioning System (GPS) balloon data.
The Doppler radars are used to detect and track the moving and stationary targets in the atmosphere. MST radar is one of the most essential apparatuses for the study of lower and middle atmosphere. The Indian MST radar can receive the Doppler echo signals from the Earth's atmosphere at the operating frequency of 53 MHz. NARL provides atmospheric wind data in the form of complex time series data by using this radar. The radar receives raw data starting from aaltitude of 3.6 km with a range resolution of 150 m up to a height of 26 km. The existing algorithm, NARL using a software tool named as Atmospheric Data Processor (ADP) (Anandan, 2001) is used for processing of MST radar data. The steps of ADP are: 1. Finding the Doppler spectrum. 2. Calculation of radial velocities. 3. Obtaining zonal, meridional components, and 4. Estimation of wind speed. The atmospheric backscattered echoes are very weak and frequently submerged with the ground clutter, interference, system bias, etc. Spectrum estimation is a fundamental problem in radar signal processing. In literature, there are many algorithms and techniques available for estimating the Doppler spectrum. An adaptive estimation technique is presented in Anandan, Balamuralidhar, Rao, and Jain (1996) to estimate the Doppler spectrum. In this technique, certain parameters are used to adaptively follow the radar signal in the range- Doppler spectral frame. Multi-taper spectral estimation (Anandan, Reddy, & Rao, 2001) and also Bispectralbased estimation (Anandan, Pan, Rajalakshmi, & Reddy, 2004) is applied to radar data, which have high computational cost and with broadened spectral peak, respectively. Other algorithms, such as cepstral thresholding (Reddy & Reddy, 2010a) and wavelet-based denoising (Thatiparthi, Gudheti, & Sourirajan, 2009) have been used for spectral cleaning and then computing the Doppler spectrum, leading to the estimation of wind velocities. In Rao, Reddy, and Reddy (2014), Principal Component Analysis (PCA) is also applied on the MST radar data, proceeding to periodogram estimation using minimum variance and Blackman-Tukey methods for spectral estimation of the MST radar signal. In (Reddy & Reddy, 2010b), uniform filter banks are also used for finding spectrum via polyphase approach. Multi-band wavelets has been applied to MST radar data for spectral cleaning (Chandraiah & Reddy, 2018). However, the available algorithms in literature were not giving consistent results at higher altitudes and even at low SNR conditions. Hence, there is a necessity to implement an efficient algorithm to estimate accurate doppler profiles. The specifications of the MST radar at NARL are shown in Table 1.
Table 1. Main Specifications of the Indian MST Radar
This section gives the description of data model used in the proposed algoritm and implementation approach of the algorithm. The complex time series data is generated to test the algorithm, which contains exponentials with three different frequencies in the presence of white Gaussian noise (AWWGN).
Let y(tn) represents the complex data obtained by weighted combination of C exponentials with frequencies.
Here, C is small number. denotes the uniform sampling time instants and {ql} denotes the amplitudes corresponding to the frequencies {Ωl} and {e(tn)} denotes the additive white Gaussian noise in the data. The continous frequency axis is sampled into R finite R number of frequency points, i.e., (ωr)Rr=1. Each of the frequency points may be represented with ωr = Ωmaxr/R. Consequently, the complex data can be written as:
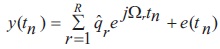
The expanded version of equation (2) is
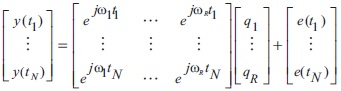
Those values of r for which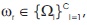 
the corresponding values will be nonzero and equal to ql. This indicates the presence of only the few frequency components, making the spectrum sparse in nature. The main problem is to find these frequencies contained in the signal. Equation (3) can be represented in the form of vector as,
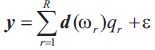
where d(ωr) is defined as N sinusoidal components with frequency ωr as
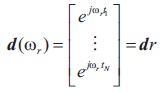
The covariance matrix of the signal has the following model:
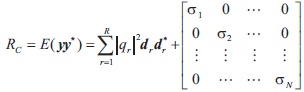
where
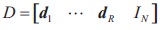
where {pi}R+Ni=1 is a replacement of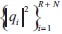 
. The first R diagonal values of matrix P denote the powers that are to be estimated, and the N diagonal values denote the noise variances. Equation (7) gives the true covariance matric Rc. Let pr(i) denote the estimate of pr at the ith iteration, and let Rc(i) be the matrix Rc made from {pr(i)}. Then IAA updates the power values by using the following iterative process (Yardibi, Stoica, Xue, & Baggeroer, 2010; Stoica, Li, & He, 2009).
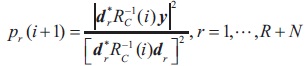
The initial power estimates {pr(0)} can be obtained by using the Single Frequency Least Squares (SFLS) method (Stoica, Babu, & Li, 2011).
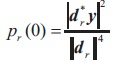
The simulation result analysis of the complex data has been presented in this section. The time series data with number of points , N=200 and number of frequencies C=3, the complex data samples are generated from exponential functions at three different frequencies of 0.3100 Hz, 0.3150 Hz, and 0.1450 Hz and having amplitudes q1=10ejφ1, q2=10ejφ2, and q3=10ejφ3 with a sampling period of 1 s. The phase values of {φ1}3l=1 are independent and uniformly distributed in [0, 2π]. The white Gaussian noise (AWGN) with zero mean and variance (σ2) is introduced in the E term. Figure 1 shows the original power spectral density of the complex signal prior to adding the noise. Figures 2(a) and 2(b) show the power spectral density of the complex signal through periodogram after adding the noise in two different Signal-to-Noise Ratio (SNR) conditions of -10 dB and 0 dB. The periodogram estimation is obtained by padding the 200 samples of data with 312 zeros and then performing the 512-FFT. For the IAA algorithm, the number of frequency points of K is taken as 512. Similarly, Figures 3(a) and 3(b) represent the Power Spectral Density of a complex test signal by using PALG for the SNR values of -10 dB and 0 dB. The main intensity of this algorithm is to estimate peak powers at actual frequencies present in the signal even if the frequencies are very close to each other.
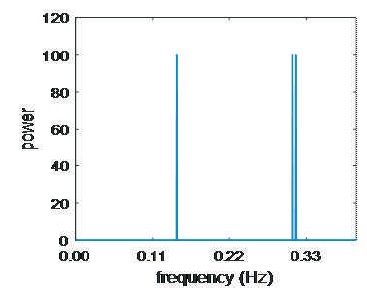
Figure 1. Power Spectral Density of Original Complex Signal
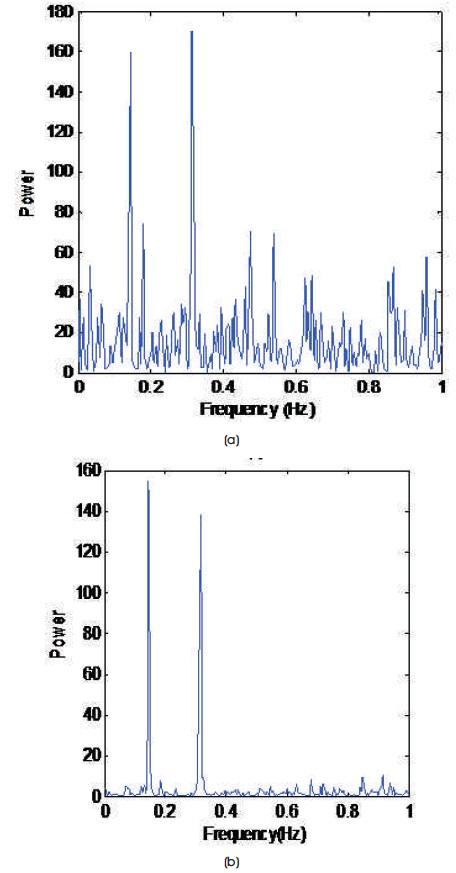
Figure 2. Power Spectral Density of the Complex Test Signal using Periodogram for (a) SNR= -10 dB (b) SNR= 0 dB
Figure 3. Power Spectral Density of the Complex Test Signal using IAA for (a) SNR= -10 dB (b) SNR= 0 dB
MST radar data contains 150 range bins; each bin has 512 complex time series data samples. The information is collected from atmosphere in six beams, viz., east, west, zenith-X, zenith-Y, north, and south. Periodogram and PALG to each bin data has been applied. Once power spectrum is estimated and maximum detection method is applied to the spectrum to extract maximum magnitude of the peak frequency and its location (index).
This process will repeat for all 150 bins in a particular beam and for all beams to a selected scan cycle.
2.2.1 Methodology for Computing Wind Components
Let Index denotes the vector of indices of frequency peaks at all range bins of a particular beam and for the particular beam, the Doppler frequency components and Doppler velocities can be calculated as:
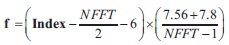
and
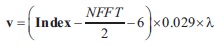
where NFFT is the FFT points and λ = c/fc, c is the velocity of light and fc is the operating frequency (53 MHz). Similarly, the Doppler profiles and Doppler velocities are computed for all six beams, i.e., fE, fW, fZx, fZy, fN, fS and vE, vW, vZx, vZy, vN, vS, respectively. The formula for computing wind velocity components using the above Doppler velocities is as follows:
where vx, vy, and vz are the zonal U, meridional V, and vertical velocity components, respectively. The vertical velocity component vz are not used in the calculation of wind speed. Hence the wind speed is computed as follows.
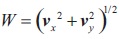
The estimated atmospheric wind speed using ELAG and PALG is validated with the corresponding wind speed collected from the GPS radiosonde data (Rao, Rao, Ratnam, Mohan, & Rao, 2003).
The height profiles estimation of Signal-to-Noise ratio (SNR) (Hooper, 1999) derived from the Doppler spectrum estimated using periodogram and PALG for the east beam are shown in Figure 4. From the Figure 4, it is observed that PALG is giving good SNR improvement at higher altitudes about 2 dB as compared to that of periodogram. Doppler frequency height profiles obtained using PALG for the east and west beams of an aforementioned radar data are shown in Figures 5 and 6, respectively. Figure 7 illustrates all six Doppler velocities of the radar data. The comparison of wind parameters like zonal U, meridional V, and wind speed obtained from the GPS data, ADP, and PALG, respectively are shown in Figure 8. From Figure 8, it can be observed that the wind speed estimated using PALG is approaching to the GPS, whereas the wind speed obtained using the ADP has deviated.
Figure 4. East Beam Height Profiles of SNR estimated using Periodogram (PER) and PALG for Radar Data on Feb 9th, 2015
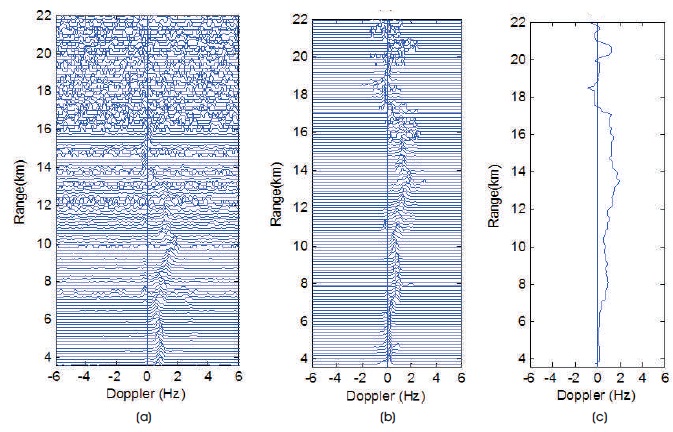
Figure 5(a) Typical Doppler Spectra of the East Beam for the Radar Data on Feb 9th, 2015 (b) After Processing (c) Doppler Profile using PALG
Figure 6(a) Typical Doppler Spectra of the West Beam for the Radar Data collected th on Feb 9th, 2015 (b) After Processing (c) Doppler Profile using PALG
Figure 7. Doppler Velocities of afermentioned MST Data
Figure 8. Comparison of Zonal U, Meridional V, and Wind Speed for the Radar Data on Feb 09th, 2015 using ADP, PALG, and GPS
Figure 9 presents the correlation coefficient analysis between wind speed from GPS data and wind speed obtained from PALG for the MST data collected on Feb 9th, 2015. The average correlation coefficient of PALG is 0.9313.
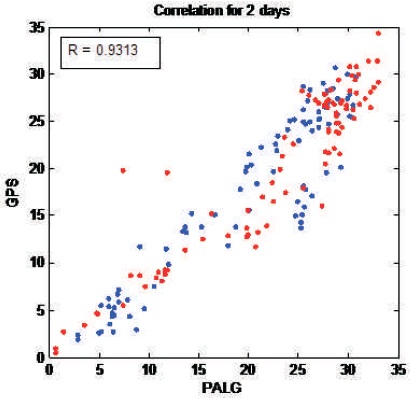
Figure 9. Wind Speed Correlation Analysis between GPS and PALG for the Radar Data received on Feb 9th and Feb 10th, 2015
In this paper, a new spectral estimation method based on iterative adaptive algorithm has been proposed. When tested on simulation data, it was found to give better results than the periodogram method (PER) at two different SNR conditions. Based on spectral density estimation of simulation signal analysis, the proposed algorithm to the Indian MST radar data collected from the NARL on Feb 9th 2015 has been applied. For processing MST radar data, NARL have been using ADP tool. Here the authors have compared the radar results for the aforementioned data with the existing Atmospheric Data Processor (ADP). Finally, the results for Zonal U, Meridional V, and Wind Speed have been validated with the GPS measurements.
The authors would like to thank the NARL, Gadanki, India for providing MST radar data and Centre of Excellence (CoE), Department of Electronics and Communication Engineering, Sri Venkateswara University College of Engineering for technical assistance.