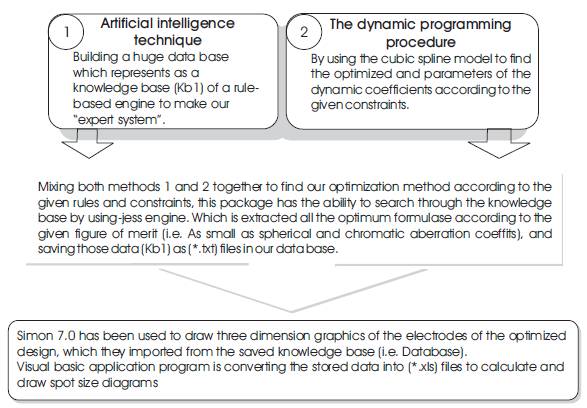
Figure 1 shows the schematic diagram of the work
A computer aided design (CAD) using optimization methods for the ion optical system has been developed, by mixing the dynamic programming procedure and artificial intelligence technique. CADION ANALYZER has been designed as an expert system, written in Java expert system shell(JESS 6.1) and Visual Basic 6 (VB6) for optimizing and analyzing full calculation processes. By using this rule based engine, the optimized axial potential distributions for electrostatic fields under imposed constraints have been used in the optical column setup. Spot size measurements were calculated in nano scales, which have values closed to (3.0) nm applicable in nano technology applications.
The increasing demand for smaller structures for fundamental physics research as well as for faster and higher density electronic circuits pushed the fabrication technology in recent years to dimensions in the nanometer-scale region. For the fabrication of structures with extremely small details both pattern definition and pattern transfer play a crucial role. The ion-beam lithography system is widely used for the pattern definition [1]. As will be shown in the present work, a simulation and optimization procedure have used to design lenses with relatively large overall dimensions of the order of a few millimeters and of a medium resolution of the order of (30 100) nm. It is aimed for finding the potential distribution that minimizes the aberration coefficients integrals, at the same time satisfying the differential equation of the paraxial rays, and also the constraints imposed by practical requirements.
In the work, a database was established to provide storage and retrieval of calculated optical properties (i.e. spherical and chromatic aberration coefficients) and optimized the electrostatic potential distributions according to dynamic programming procedure mixed with an expert system, which has been built according to artificial intelligence technique rulebased system [2]. It maintains a collection of knowledge nuggets called facts. This collection is known as the knowledge base, which is our relational database. By using a Jess 6.1 (i.e. Java Expert System Shell-version 6.1) programming language and a class modules in VB 6 (i.e. visual basic studio - version 6) the present work expert system has been created and setting up the user interface.
Our rule based expert system written in Jess is a data-driven program where the facts are the data stored in our knowledge base that stimulate execution via the inference engine. This engine decides which rules should be executed and when [3]. Therefore, the present expert system automatically performs the field calculation and ray tracing, depending on the stored data base (i.e. jess knowledge base) and the following two factors:
The subroutines comprise of our full package (CADION) which stands for (Computer Aided Design for ION system) as described as a class module program written in jess 6.1 and visual basic 6 and designed as one simulator as follows:
The spherical and chromatic aberration coefficients have been calculated within the CADION simulations, which gives the main indications for building the electrodes design of each model. Different cases of electrostatic lenses have been investigated in this work. Many factors and variables have to be calculated to make sure any of results among the others corrected. Those factors have used optimizing process supported by artificial intelligence technique. So that, considerable amount of errors obtained were neglected in the accumulation of data. Obviously, most of the formulae were optimized in the CADION simulator subroutines. To make fitted comparisons, a well known simulator SIMION 7.0 package has been used for importing data resulted by CADION stored database to figure out the optimized results, and plotting the electrostatic lenses electrodes in three dimension profiles. Figures (1) and (2) show the schematic diagram and the data flow chart of the optimization steps of our investigation, respectively.

Figure 1 shows the schematic diagram of the work
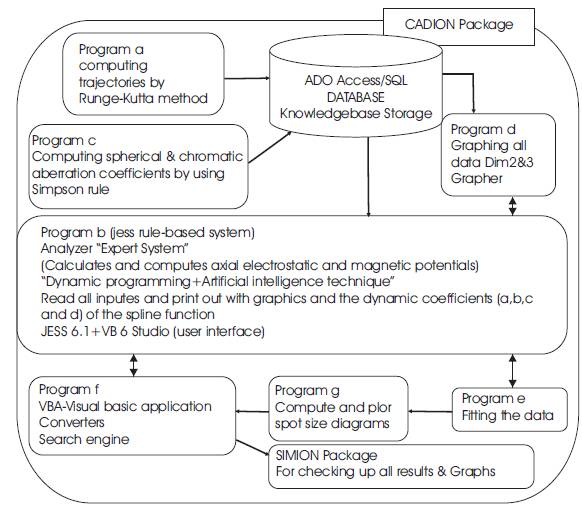
Figure 2 represents the optimization schematic diagram of the present work software.
In recent years, most of the researchers have been interested in optimizing optical instruments and devices as a nano scale devices. Also, they attempted the design and optimization of electron lenses and systems according to the analysis method with the aid of computer programs, where symbolic computing has become a promising aid in different kinds of decision making. Expert systems that have built in knowledge in the form of symbolically represented facts and rules. Steve et al 1993 described a novel method of determining potentially successful starting designs by utilizing expert systems algorithm which operates on a database of previously well-designed optical systems [5].Also, Xiaogang Chen et al 1993 developed a small expert system used in lens design [6].
According to Szilagyi [1977, 1978], who introduced the dynamic programming approach [7], and more recently to Ahmad et al 2002, have introduced a computer aided design of an electrostatic FIB system consisting of three electrostatic lenses approximated by the spline lens model [8]. Our rule-based has been used as the procedure (i.e. jess rule based) for the typical dynamic programming recursive formulation as [9]:
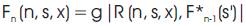
where n is an integer denoting the stage of the problem, s is an integer denoting the state of the system at n, s' is an integer denoting the state of the system at stage n-1 resulting from the decision x, x is the decision being evaluated at stage n , R(n,s,x) is the immediate return associated with making decision x at stage n when the state of the system is s , F* n-1(s') is the return associated with an optimal sequence of the decision at stage n-1 when the state is s' and g is the minimal function. Figure (3) shows the computational grid for the dynamic programming procedure with the aid of artificial intelligence technique. It defined the domain of existence of the solution for the sought distribution function W (z) (i.e. electrostatic field).
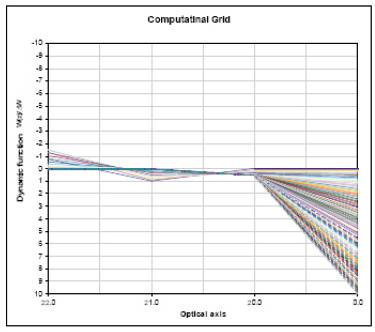
Figure 3 represents computational grid of the dynamic programming procedure with the aid of artificial intelligence technique for electrostatic lenses defined over twenty intervals.
Four types of the optimum axial potential distributions with their first derivative have been determined for designing the electrostatic lenses, by using the dynamic programming procedure and artificial intelligence technique operated with the acceleration and deceleration modes depending on the imposed constraints, are shown in figures (4, 5, 6 and 7). Table (1) gives the optimized formulae and their dynamic parameters according to our rule based CADION ANALYZER (i.e. program "b") as in equation (1).
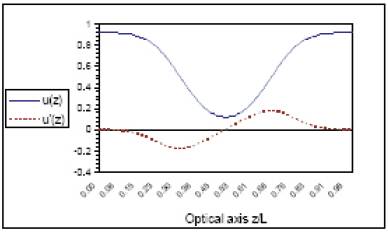
Figure 4 the optimum axial potential distribution and its first derivative u(z) and u'(z) respectively for unipotential lens (1) operated in deceleration mode.
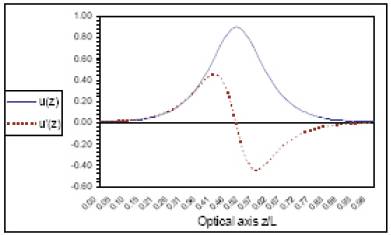
Figure 5 the optimum axial potential distribution and its first derivative u(z) and u'(z) respectively for unipotential lens (2) operated in acceleration mode.
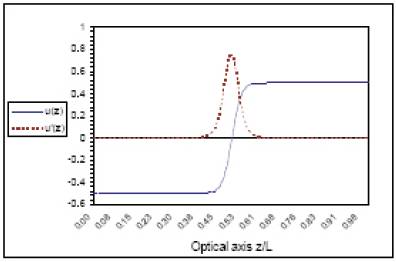
Figure 6 the optimum axial potential distribution and its first derivative u(z) and u'(z) respectively for immersion lens.
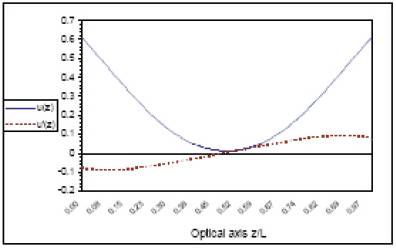
Figure 7 the optimum axial potential distribution and its first derivative u(z) and u'(z) respectively for diaphragm lens.
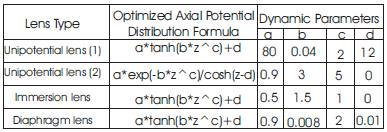
Table 1 the optimized axial potential distributions with their dynamic parameters for two electrostatic lens types
SIMION 7.0 simulator is used for plotting the electrodes profiles of such lenses in three dimensions. Figures (8), (9), (10) and (11) show the optimized lens electrodes of (unipotential lens (1), unipotential lens (2), immersion lens and diaphragm lens), respectively.
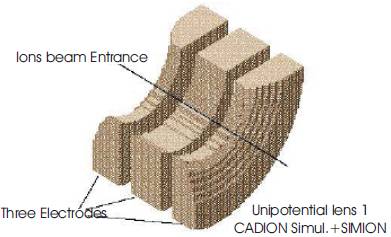
Figure 8 the electrodes profile of unipotential lens (1).
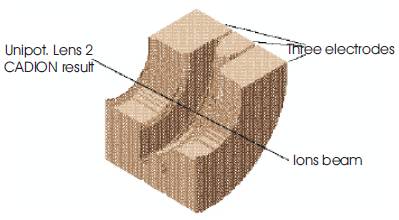
Figure 9 the electrodes profile of unipotential lens (2).
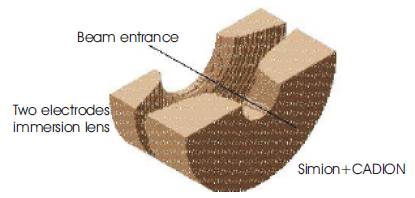
Figure 10 the electrodes profile of immersion lens.
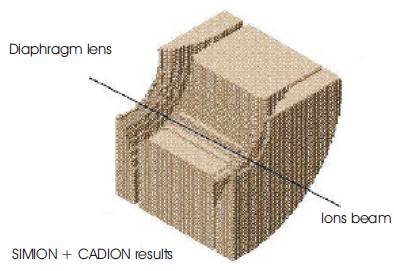
Figure 11 the electrodes profile of diaphragm lens.
Demagnification of the beam size in the image plane is one of the most important requirements of focused ion beam, which should be associated with low aberrations. The ion beam system consisting of three lenses with a beam crossover is taken the following setup:
The ion beam trajectories are shown in figures (12) and (13), respectively.
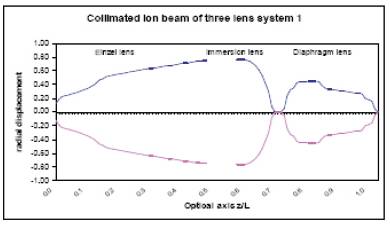
Figure 12 The ion beam trajectory for a three-lens system (1).
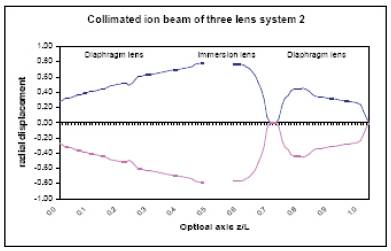
Figure 13 The ion beam trajectory for a three-lens system (2).
By using CADION package the spot size has been calculated, figure (14) shows the spot size calculations for a range of beam angles [5, 10,30,50,75, and 100] mrad of the given ion beam three-lens systems. It is clear from the figure that the nano scale spot size focusing for ions in the image plane have values which are very useful for getting FIB designing .
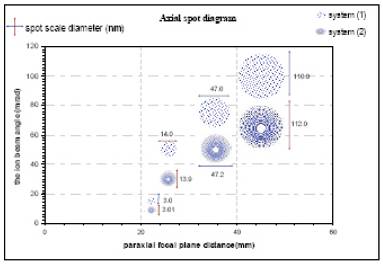
Figure 14 the axial spot size measurements versus the beam angle for three-lens systems.
The present investigation has clearly adopted a combined optimization procedure by adding the dynamic programming procedure and the artificial intelligence technique, which was mixed to find a smart simulator, packed in one program (i.e. expert system). This significant computational work was made to get CADION package. The significant rule based expert system is the CADION ANALYZER (i.e. program"b"), which comprise the facts of our calculations, and our results have been obtained according to this rule based system.
Also, nano scale measurements of spot size focusing for ions in the image plane have values which are very useful for getting FIB designing. Over a range of ion beam angles (5, 10,30,50,75 and 100) mrad, the results were from 3nm to few tenths of nanometers.
We would like to thank College of Science at Al-Nahrain University for supporting this work. Multi thanks to SIMION research group at SIMION Company for delivering a test compiler of SIMION package and helping us to check our results.