Cyclone separators are widely used for separating solids from air-solid mixture. Cyclones can also be used as heat transfer equipment for drying, solidification, sublimation, reactions, etc. Centrifugal force is the driving force for separation of solid particles of various sizes from air stream. Collection efficiency of cyclone is found to increase with increase in particle size. The cyclone is a settling chamber in the form of a vertical cylinder, so arranged that the particle-laden air spirals round the cylinder to create centrifugal forces which throw the particles to the outside walls. Added to the gravitational forces, the centrifugal action provides reasonably rapid settlement rates. The air stream is injected at high velocities into the inlet pipe, which is positioned tangentially to the body of the cyclone. Gas entering the cyclone takes a tangential path and starts moving along the circumference. Gas inside cyclone has velocities in three directions. These are axial, radial & tangential. Tangential velocity is of order of inlet velocity. Radial velocity is high at low solid flow rates which results in bypass of gas from the outer vortex into the inner vortex without reaching the bottom. The axial velocity is responsible for movement of gas from top to bottom of cyclone and then into the inner vortex. The axial velocity is high & is independent of gravity. Yen et al. (1990) and Raju et al. (1994) reported experimental investigations on air-solid heat transfer in reverse flow cyclones and proposed correlations for gas-solid heat transfer in cyclone which can be reliably used for design of cyclone for commercial applications.

Cyclones can be used for heating solid particles where direct contact with gas is permitted. Since it has potential applications as heat exchangers in fertilizer, polymer powder, pharmaceutical and other industries, study of cyclone as heat exchanger is gaining attention [Szekely 1966]. In present study, experiments are conducted in a cyclone heat exchanger of 160 mm diameter, using sand. The effects of solid feed rate (0.01-0.025 kg/s), cyclone inlet air velocity (5.44-9.1m/s), and particle sizes (196-725 μm) on heat transfer rate, exit solid temperature, heat transfer area and heat transfer coefficient were studied. An empirical correlation was proposed for the prediction of heat transfer coefficients based on experimental data. The heat transfer coefficients obtained by correlation in the present study were compared with literature values.

1.1 Experimental Setup

The experimental set up is shown in Figure 1. It consists of an air inlet pipe with heating coil, solid feeding system hopper, cyclone separator and a blower. Air flow rate was measured by venturimeter fitted with U tube manometer with its two ends connected at inlet pipe and throat respectively. U tube was filled with water as a manometric fluid. Thermocouples were connected to measure inlet and exit temperatures of solid and which indicated on digital temperature indicator. Heater temperature was adjusted with the help of controller such that heated air is  available at 120^o C. Solid receiver was provided at the bottom of separator. Heating coil of 2000 Watt was woven on a marble plate of 8 cm width and 38 cm length by drilling holes on plate and it was inserted into pipe such that coil was not touching pipe at any point hence sufficient clearance was provided. Whole system was insulated with two layers of thick 6 mm asbestos insulation to avoid heat losses. Particles of four different average sizes were screened and analysis is given in Table 1.

Figure 1. Experimental; Set-up

Table 1. Screen Analysis

1.2 Experimental Procedure

• Air flow rate was adjusted to desired value with the help of inlet valve.
• Air was drawn from ambient by blower and heated to 120^o C by passing through heating coil.
• Heated air was passed through the system for about 1 hour to achieve steady state.
• Particles of particular average size were fed into system at desired flow rate by adjusting opening by valve at bottom of hopper.
• A steady solid feed rate was achieved for a particular combination of particle size and gas velocity.
• After desired period of operation, air flow, solid flow and heater was shut off.
• Exit temperature of air and solid was noted by digital temperature indicator.
• Hold up of particles was measured by simultaneously closing air flow, solid flow and heater.
• Same procedure was repeated for particles of different sizes at different solid flow rates and air flow rates.

1.3 Parameters Studied

Air was employed as a carrier gas throughout the experiment. The ranges of the various parameters used are given in Table 2. Sand particles of four different sizes 725 μm, 512.5 μm, 362.5 μm and 196 μm were used.

Table 2. Range of various parameters used

1.4 Theory

Volumetric flow rate of air (q) through venturimeter is given by,

(1)

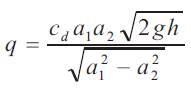
Where,

c_d = Coefficient of discharge,

a₁ = Cross sectional area of inlet pipe.

a₂ = Cross sectional area of throat,

h = Difference of pressure head.

In present study, gas and solids move parallel in same direction, the cyclone can be considered as concurrent heat exchanger. Log-mean temperature difference is defined as,

(2)

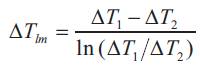
Where, ΔT₁ = T₁ – t _i, ΔT₂ = T₀– t₀ T₁ = Inlet temperature of air, t_i = Inlet temperature of sand, T₀ =Outlet temperature of air, t₀ =Outlet temperature of sand

Heat absorbed by sand,

(3)

Where, W_s = Solid flow rate (kg/s), C_ps =Specific heat of sand (J/kgK)

The heat transfer area A is the total surface area of the particles in the cyclone at any instant of time. It is related to hold up (M), density (ρ_s) and size of the particles (d_p ) as given below,

(4)

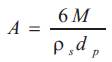
The gas-solid heat transfer coefficient (h) is defined as,

(5)

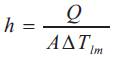
By above equation experimental heat transfer coefficient is calculated.

In present work, flow in cyclone was considered as a plug flow. Yen et al. (1990). confirmed it experimentally by observing the flow patterns in a transparent cyclone and measured the particle residence time distribution in the cyclone. Szekely and Carr (1966) also confirmed the plug flow of iron particles in the cyclone. In present study, experiments have been carried out by supplying hot air at constant as well as variant velocity to observe the effect of solid flow rate on exit solid temperature, heat transfer rate, heat transfer area and heat transfer coefficient for different particles of four sizes.

2.1 Constant inlet air velocity

Figure 2 indicates that for a particular size particles, exit solid temperature increases with increase in solid flow rate up to certain solid feed rate after which exit solid temperature decreases. The quantity of bypass air from outer to inner vortex governs the air available for heat transfer to solids in the outer vortex and the rise in solid temperature. With reduced bypass at higher solid feed rate, more gas at high temperature was available at the bottom, resulting in increased solid temperature. This was occured till the increase in solid feed rate exceeded the reduction in air bypass, after which the exit solid temperature was decreased.

Total heat transfer area (eq. 4) was higher for smaller size particles at constant solid feed rate. As heat picked up by a particle was directly proportional to the area of the particle, smaller particles at the same feed rate were in a position of advantage than the bigger particles. Hence, the smaller particles pick up more heat and the exit temperature was increased for smaller size particles than larger at same solid feed rate.

Figure 3 indicated that with increase in solid flow rate for the particles of particular size, bypass of air was decreased and more air reached the bottom of the cyclone. Since more air at high temperature was available at the bottom of the cyclone at high solid flow rates, driving force for heat transfer was large hence, heat removal rate increased. As particle size reduced, heat transfer area was increased hence heat removal rate increased.

Figure 4 indictated that heat transfer area increased with increased in solid feed rate. Solid feed rate was proportional to hold up of particles. Hence, for a particular size particles, with increased in solid feed rate, hold up was increased and hence heat transfer area increased. Heat transfer area was inversely proportional to particle size. Hence it was higher for smaller particles for same solid feed rate.

Figure 5 represented that heat transfer coefficient increased with increased in solid flow rate for the particles of particular average size. Heat removal rate and heat transfer area were increased and ΔT_lm decreased with increase in solid feed rate. Hence heat transfer coefficient increases with increased in solid flow rate for the particles of particular average size up to certain stage then it was decreased due to decreased in exit solid temperature. Raju et al. (1994) and Pawar and Bhaskara (1988) made similar observations. Larger particle sizes decreased heat removal rate and heat transfer area in such a way that heat transfer coefficient was increased. Hence, with larger particle sizes, higher heat transfer coefficients were achieved.

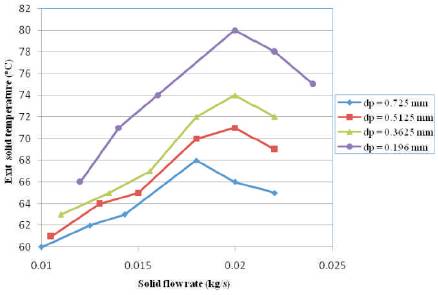
Figure 2. Effect of solid feed rate on solid exit temperature at constant inlet air velocity (V=7.92 m/s)

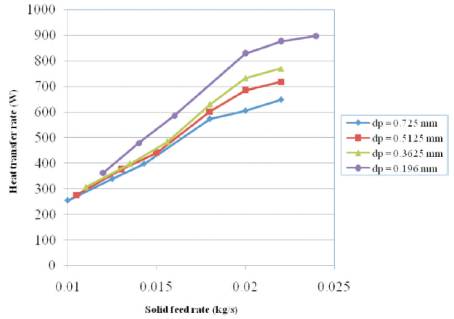
Figure 3. Effect of solid feed rate on heat transfer rate at constant inlet air velocity (V=7.92 m/s)

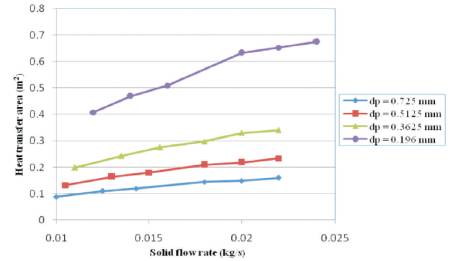
Figure 4. Effect of solid feed rate on heat transfer area at constant inlet air velocity (V=7.92 m/s)

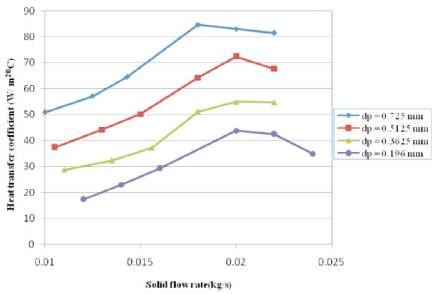
Figure 5. Effect of solid feed rate on heat transfer coefficient at constant inlet air velocity (V=7.92 m/s)

2.2 Variant velocity

Figure 6 indicated that exit solid temperature was increased with the increase in inlet air velocity at constant solid feed rate. This was observed for particles of all sizes and at all solid feed rates. With increased in inlet air velocity, mass flow rate of air was increased hence, heat capacity of air increased. Due to the increase in heat capacity of air at higher inlet air velocities, more gas at high temperature was available at the bottom for the heat transfer. As a result of this, solids extract more heat from the gas, resulting in increase in the solid exit temperature due to the thermal balance between gas and the solid. With reduced bypass at higher solid feed rate, more gas at high temperature was available at the bottom, resulting in increased solid temperature. This was occurred till the increase in solid feed rate exceeded the reduction in air bypass, after which the exit solid temperature was decreased.

Figure 7 presented that heat transfer rate was increased with the increase in inlet air velocity at constant solid feed rate. This was observed for particles of all sizes and at all solid feed rates. As the inlet air velocity was increased at constant solid feed rate, mass flow rate of air increased. Hence heat capacity of the air increases. Therefore, with the increase in heat capacity of air, decrease in temperature of air was less. Subsequently, gas was available at high temperature at the bottom resulting in increased driving force. Heat transfer area also increased with increased in air velocity due to increased in hold up. Hence, due to combined effect of increased in solid exit temperature and heat transfer area, the heat transfer rate also increased.

Figure 8 indicated that heat transfer area was increased with the increase in inlet air velocity at constant solid feed rate. This was observed for particles of all sizes and at all solid feed rates. With increased in inlet air velocity, hold up of particles increased hence, heat transfer area increased.

Figure 9 indicated that the heat transfer coefficient was essentially independent of inlet air velocity for a given solid feed rate. This behavior was observed for all sizes of particles at all solid feed rates. Increased in heat transfer rate, heat transfer area with increase in air velocity was such that net effect on heat transfer coefficient was nullified. Yen et al. (1990), Jain et al. (2006), Chang and Wen (1966)made a similar observation. Hence, it can be concluded that the heat transfer coefficient is essentially independent of inlet air velocity.

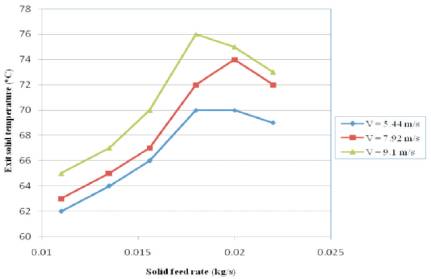
Figure 6. Effect of solid feed rate on exit solid temperature at different inlet air velocities for average particle size of 362.5 μm

Figure 7. Effect of solid feed rate on heat transfer rate at different inlet air velocities for average particle size of 362.5 μm

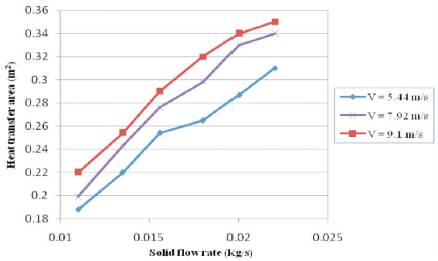
Figure 8. Effect of solid feed rate on heat transfer area at different inlet air velocities for average particle size of 362.5 μm

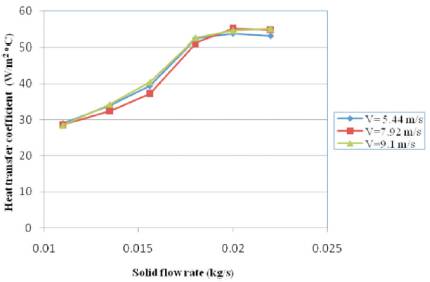
Figure 9. Effect of solid feed rate on heat transfer coefficient at different inlet air velocities for average particle size of 362.5 μm

2.3 Comparison of Heat Transfer Coefficient with Literature Correlations

Raju et al. (1994) conducted heat transfer studies in a reverse flow cyclone of 130 mm diameter for air- sand System. Correlation for heat transfer coefficient in terms of Nusselt number, Reynolds number, Prandtl number and solid-gas mass flow ratio is given as,

(6)

Where,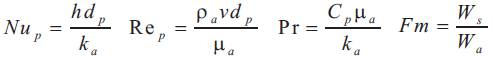

Yen et al. (1990) conducted heat transfer studies in a reverse flow cyclone of 120 mm diameter for air- sand System. Correlations for heat transfer coefficient in terms of Nusselt number, Reynolds number, Prandtl number & Solid-Gas mass flow ratio is as given below,

(7)

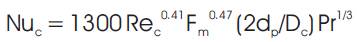
Where,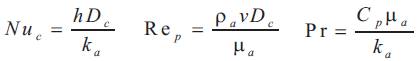

Using equations 6 and 7, heat transfer coefficient were calculated.

The correlation of Yen et al. (1990) consistently over predicted the data within an error band of 50%—15%.

The trend of the predicted heat transfer coefficient was matched with the experimental data. However, all the predicted values are higher by a factor of about 1.5. The correlation of Raju et al. (1994) predicted the present data within 17% to —10%.

The heat transfer coefficients predicted by Eq. (6) were compared with the experimental data (Figure 10).

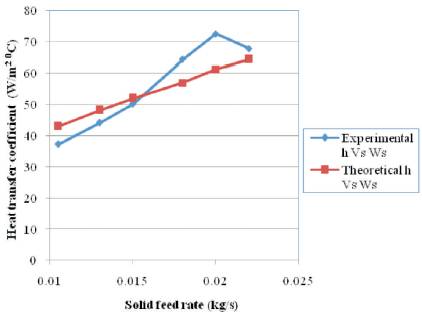
Figure 10. Effect of solid feed rate on experimental and theoretical heat transfer coefficient for average particle size of 512.5 μm at constant inlet air velocity (V=7.92 m/s)

2.4 Development of a New Correlation

Nusselt number, Reynolds number and Prandtl number have been widely used to correlate gas-particle heat transfer coefficient. The particle Reynolds number was computed based on cyclone inlet air velocity. The flow inside a cyclone was very complicated because of its three-dimensional nature and presence of tangential, radial, and axial velocity components. In the vicinity of the wall, where most of the particles were present, the tangential velocity was approximately equal to the gas velocity on entry. Hence, the inlet velocity was used as the characteristic velocity in the particle Reynolds number.

Heat transfer coefficient is a function of particle size and cyclone diameter. With increase in particle size, heat transfer coefficient increases. By decreasing cyclone diameter, heat transfer rate and hence heat transfer coefficient can be increased. Hence, new correlation is developed on the basis that heat transfer coefficient is a function of particle size and cyclone diameter in addition to Reynolds number, Prandtl number and solid air mass flow ratio. The heat transfer coefficient can be written as:

h = f (p_a , d_p , k_a , µ_a, F_m , D_c , V, C_pa )

Number of terms = 9, Number of repeating variables = 4

Number of П terms = 9-4 = 5

By using Buckingham's П theorem for dimensional analysis, π terms are found as,

 

It can be seen that П₁ = f(П₂, П₃, П₄, П₅)

Hence Nu_p = f (Re_p , P_r, F_m , d_p /D_c )

Assume, Nu_p = a (Re_pb ) (Pr_c ) (F_md ) (d_p /D_c )

Constants a, b, c, and d were found from experimental data and these are:

Hence proposed new correlation for finding heat transfer coefficient is:

(8)

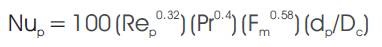
Heat transfer coefficient obtained by proposed correlation was compared with experimental heat transfer coefficient and theoretical heat transfer coefficient obtained by Raju et al. (1994) correlation (Figure 11). The heat transfer coefficients obtained in the present study matches with theoretical heat transfer coefficient obtained by Raju et al. (1994). correlation within an error band of 17% to —10% and that of proposed correlation within an error band of +10% to —8%. Results are also comparable with the results of Jain et al. (2006).

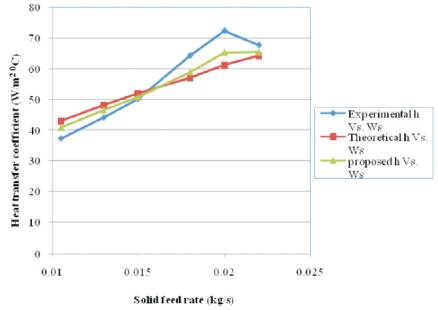
Figure 11. Effect of solid feed rate on experimental, theoretical and proposed heat transfer coefficient for average particle size of 512.5 μm at constant inlet air

The following conclusions were drawn from the present study of air-to-solid heat transfer in a cyclone:

• Heat transfer rate increased with increase in solid feed rate, inlet air velocity, and decrease in particle size.
• Exit solid temperature increased with increase in solid feed rate up to certain critical value and then decreased further. Exit solid temperature increased with increase in inlet air velocity, and decrease in particle size.
• Heat transfer area was increased with increase in solid feed rate, inlet air velocity, and decrease in particle size.
• Heat transfer coefficient between air and the solid particles was increased with increase in solid feed rate and particle size. But heat transfer coefficient was found to be essentially independent of air velocity.
• Heat transfer coefficients obtained in the present study was matched with theoretical heat transfer coefficient obtained by Raju et al. (1994). correlation within an error band of 17% to-10% and that of proposed correlation within an error band of +10 to -8%. This appears to be an improvement over the correlations proposed by Yen et al. (1990). and Raju et al. (1994).