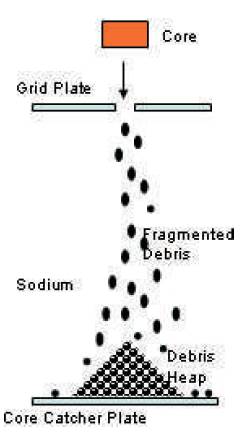
Figure 1. Core Debris on Core Catcher Plate
Dimensional analysis consists of identifying parameters influencing any process and grouping them into a set of independent dimensionless numbers using Buckingham's pi theorem. It is a powerful tool for correlating data obtained from experiments where each of the controlling parameters is systematically varied.
In this case study, dimensional analysis is applied to study the heap forming characteristics of the core debris generated during a Fuel Coolant Interaction (FCI) following an accident in a fast breeder reactor. The study of debris heaping behaviour on the corecatcher plate is important from recriticality concern and also from cooling considerations to ensure the safety of the reactor main vessel after the accident. The debris heap is characterized by the static repose angle. The complete set of dimensionless groups defining the heaping phenomenon is derived. It is shown that repose angle of the heap is a function of Particle Reynold's number (Re), Froude number(Fr) and Archimedes number (Ar) for a system with geometry and density similitudes.
A set of experiments is conducted with lead spheres in water to mimic the heaping behaviour of core debris on corecatcher plate in sodium, their density ratio being similar. The repose angle is extracted from the digital image of the heap. From the experimental data, the functional dependence of repose angle on Re, Fr and Ar is determined and an empirical correlation is developed using regression analysis.
Dimensional analysis is identified as the basic key element in scaling philosophy used in severe accidents research program (Holowach, et al., 2003, Novak Zuber et al., 1998,) and also in the design of reduced size test facilities (Celso, 2004, Velusamy, 2001, Wolfgang Wulff, 1996,Kocamustafaogullari et al., 1983) for a nuclear reactor because it facilitates scaling down a phenomenon occurring in the prototype to experimentation in the laboratory with the option of using different working materials and fluids. If a scale model is built, the results obtained from such scale experiments can be meaningfully superimposed on the prototype via the scale factors (Schuring, 1977). On the other hand, dimensional analysis also offers the scope of correlating experimental data obtained by carrying out a series of experiments by systematically varying each of the independent variables.
The objective of the present analysis is to derive dimensionless groups for the phenomenon of spherical particles falling in a quiescent pool of water forming a heap, with particular emphasis on the final repose angle on a flat collector plate. The dimensional analysis starting with identification of important parameters, derivation of similarity groups and finally establishing functional relationship between them by an empirical correlation for the above stated phenomenon is presented in this paper.
John P Arhens (John P Arhens, 2003) in his work has correlated particle Reynolds number(Re) with Archimedes number (Ar), putting forward the idea that Ar is the only independent parameter affecting particle velocity. Paulo (Paulo N. Baptista, 1997 in his analysis of flow of spherical particles in straight tubes obtained an expression of linear velocity as a function of generalized Reynolds, Archimedes and Froude numbers, to the particle-to-fluid density simplex and to the particle tube diameter ratio.
In the reactor accident scenario, the debris heap formed on the corecatcher plate is characterized by its static repose angle. Hence, in the present study, repose angle which is the angle made by the heap with the horizontal direction is expressed in terms of other dimensionless numbers which are involved in heaping phenomenon.
A severe accident such as core disruptive accident in a Fast Breeder Reactor (FBR) is a rare occurrence, the probability of occurrence being <10-6 /reactor year. Even though it is a beyond design basis accident, engineered safeguards such as the core catcher plate are provided to mitigate the consequences of such an accident. Molten Fuel Coolant Interactions (MFCI) can happen in a FBR when there is a severe accident in the reactor in which the fuel contained in the core can melt and come in direct contact with the coolant, after breaching the grid plate. Though nuclear fission reaction ceases, the core debris continues to generate heat from the decaying fission products. The core debris finally settles on the core catcher plate where its decay heat is removed by natural circulation of the coolant. The accident scenario is pictorially represented in Figure 1.

Figure 1. Core Debris on Core Catcher Plate
In the safety analysis of FBRs, Molten Fuel Coolant Interactions are analysed for their potential to cause hazard from the coolability aspect and from the reconfiguration aspect. This means that dry out of sodium should not happen within the debris bed and the mass of the debris should not become recritical to start a fission reaction again. The size of the debris and the repose angle on the core catcher govern these two aspects.
The objective of the analysis is to derive dimensionless groups for the core debris heaping phenomena and develop correlation between them from model experiments conducted. Heap formation was studied by allowing the Lead sphere to fall on a circular plate. Single component single size debris alone is dealt in this study with water. Lead is used as a simulant material since its density is close to that of UO2 and the viscosity of water at elevated temperature is close to that of hot sodium. The influence of debris drop height, fluid properties and granular mass flux are investigated. Angle of heap is measured and its functional dependence on influencing parameters is derived.
In Europe, research program has been carried out by CEA where copper spheres in water have been used to study the heaping phenomenon and the results extrapolated to the UO2 -Na system (Moller, 1982). The maximum angle of repose measured in air was 30o and that with water was 23o . In the corecatcher design of SPX1, heaping of debris was considered assuming that particles come from one spot on the lower plate of grid plate and the angle of repose was 24o (Le Rigoleur, 1982).
A flat debris bed poses fewer problems from the recriticality point of view and also for cooling purposes. The geometrical shape of the debris bed influences the neutron multiplication factor keff upto fuel mass of about 20 tons above which the shape of the debris bed plays no role (Bhaskar Rao, 1994). This study of fuel debris heaping on the core catcher plate would help the reactor physicist in determining keff of the relocated core debris in a more accurate manner – taking into account the angle of repose of the debris on the core catcher, instead of assuming a flat or cylindrical profile.
Thermal-hydraulic analysis of corecatcher system also requires the radial extent of spreading of debris on the core catcher as input in order to estimate the temperature distribution on the core catcher plate. Hence the need was felt to assess the heaping pattern of core debris on the core catcher.
Buckingham's Pi theorem states that if there are n variables in a problem and these variables contain m primary dimensions (for example M, L, T) the equation relating all the variables will have p (p=n-m) dimensionless groups. Buckingham referred to these dimensionless groups as π groups (Perry, 1984). The outcome of dimensional analysis is the following equation:
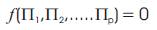
The functional dependence between these dimensionless groups has to be established from model experiments. The dimensionless groups can be manipulated amongst themselves to form many possible groups but the number of independent groups remains the same.
Dimensional analysis is performed to study experimentally the fuel debris levelling behaviour during its fall on the core catcher plate and to find out the angle of repose. Angle of repose is defined as the angle formed by the heap with the horizontal base.
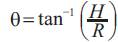
where H is the height of the heap and R is the radius of the heap.
As the granular particles fall through the liquid and get collected on the collector plate, the heap initially builds up till it reaches repose angle and then relaxes through continuous or discrete granular avalanches for further mass influx. In the post accident scenario, main interest lies in the final static angle of repose of debris.
Dimensional analysis is performed to arrive at the pi numbers that influence the final settling behaviour of small particulates which are allowed to fall through a fluid. The parameters influencing the heaping behaviour are enumerated by identifying the forces acting on the system and picking the variables from them. The equation of motion for a spherical particle falling under gravity in a pool of liquid is given by
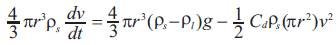
The forces acting on the particulate are gravitational, inertial, drag and viscous forces. Apart from the forces acting on the particle, the total mass of the spheres and the height of the falling column also play a crucial role in deciding the heap formation. Therefore the parameters influencing the heaping phenomenon are listed as m, v, d, , , R, H, h,, t and g where the symbols represent mass, velocity, diameter and density of the particle, density difference between particle and the fluid(-f ), radius of the heap, height of the heap, height of fall, viscosity of the fluid, time taken to reach the plate and acceleration due to gravity respectively.
The dimensions of all these quantities can be expressed using the MLT system. There are 11 parameters and 3 primary quantities. Hence 8 pi numbers would emerge from the dimensional analysis, as shown in Table 1 according to Buckingham's pi theorem. The angle of repose (π8 =H/R) can be expressed by a functional relationship among the remaining seven pi numbers.
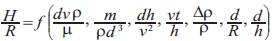
Or equivalently

The physical significance of the pi numbers are illustrated in Table 1.
The pi numbers are rearranged to get the ones which shed more light on the underlying physical phenomena. The last three pi numbers signify geometrical similarity. The number π1 can be identified as the particle Reynold's number which is the ratio of the particle inertial force to the liquid viscous force. π3 is the reciprocal of square of Froude number.
We get another useful pi number called the Archimedes number (Ar) from π1 π3 and π5. Now, Ar can replace any one of the three from the entire set.
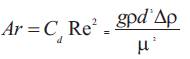
Arichimedes number replaces π5 which is allowed by Buckingham's theorem and the total number of independent groups remain the same.
Equation (4) can be rewritten as


Table 1. Pi numbers
Experiments are conducted with alternate materials because of the safety restrictions involved in handling UO2 and Sodium. Lead being a heavy metal whose density is closer to that of UO2 , it can serve as the substitute. Since heap formation only is to be evaluated neglecting the heat transfer aspects, water is a good substitute for sodium because density of water is quite close to that of sodium. Hence Lead spheres in water are chosen to duplicate the behaviour of UO2 debris in sodium. The value of 5 for the UO2 -Sodium system is 0.92 and that for Lead-water system is 0.91. Thus density ratio is preserved in the model as in the prototype.
From the particle size distribution of UO2 debris obtained from in-pile experiments at Power Burst Facility, Idaho it was observed that 90 % of the particles contained Uranium with sphericity of 75 % (Hobbins, 1982). The size of the core debris is observed to be of the order of a millimeter.Therefore spherical lead particles are used in the experiments instead of UO2 debris matching the size and shape criterion satisfactorily. Inter granular interactions are determined by coefficient of restitution which is 0.25 for UO2 particle to particle and particle to wall interactions in dry condition (Mikio Sakai, 2005). In a liquid medium, coefficient of restitution comes down further as evidenced from experiments on different materials conducted by Gondret et al (Gondret et al, 2002). Lead spheres in general show plastic behaviour with coefficient of restitution being practically zero. Therefore heap forming tendency for lead spheres will be slightly higher than that of UO2 spheres.
In the real accident scenario, the core debris will generate decay heat. The implications of neglecting heat transfer in the present analysis have to be understood from the safety perspective. Boiling of the coolant in the heat generating debris bed will lead to bubble formation, collapse within the bed or escape from the bed which can disturb the bed further leading to leveling i.e., reduction in the angle of repose. Therefore, analysis of debris bed formation without addressing heat transfer will yield a higher repose angle which can be safely taken as the upper bound for the configuration of the core debris.
Experiments were carried out to study the heaping behaviour of small Lead spheres in water. Lead shots of diameter 1.8mm, weighing 1.7kg were allowed to fall through a funnel on a circular plate to form the heap. Lead spheres were filled in the funnel after plugging the release hole by inserting a stopper rod with a conical end, which prevented the spheres flowing out during filling. The spheres were released on to the experimental plate by lifting the stopper rod. A water tank of size 27 X 36 X 38 cm was used to assemble the setup and the level of water was maintained at 1cm above the release point.
The experiments were carried out at drop heights of 50 mm, 100 mm, 150mm and 200 mm from the tip of the funnel to the surface of the collection plate. For 100 mm drop height, runs were carried out at room temperature and also at elevated water temperatures of 50oC and 70oC. The mass flux was also varied in the range of 50 gm/s to about 350 gm/s with the three funnels of different diameters. The temperature of the water bath was monitored with an RTD indicator having an accuracy of 0.3oC. Initially water was heated to a higher temperature than the required temperature with an immersion heater and then allowed to cool to the desired water temperature.
The schematic of experimental setup is shown in Figure 2. Digital snapshots of the heap were taken after each experiment. Conventional methods of measuring heap height are either to place a graduated sheet of paper vertically at the back side of the heap and make visual measurements or to use a movable pointer attached to a graduated screw. The first method is prone to parallax error and the second one is strenuous, time consuming and there is a possibility of the heap being disturbed when the pointer is made to touch the heap.
Hence, it is proposed to extract the angle of repose and height of the heap from the digital snapshot of the debris heap. The advantage of this method is that it is non invasive and does not disturb the heap.
The heap profile and heap angle have been obtained by processing the pictures in Microsoft-Photo Editor. The heap angles were deduced with a resolution of 0.20. The diameter of the plate in the image is taken as reference scale to get the absolute values of the heap profile. A stopwatch was also used to time the heap forming event from which the granular mass flow rate is estimated. A typical digital snapshot of the image is shown in Figure 3.

Figure 2. Schematic diagram of experimental setup

Figure 3. Image of the Lead Shots Heap
The collector plate is seen mounted on an adjustable platform. The extreme ends of the plate whose diameter is known serves as reference for the conversion of pixel to mm. The image is downloaded to PC and saved in jpg format. Using an image viewing tool like MS photo editor, the position of cursor on any point of the image could be read in terms of pixels. The user has to click over the image to select a point. The heap height above the rim is measured by reading the y coordinate of the point corresponding to the heap peak and that corresponding to the rim of the plate and converting the pixels to mm. The actual heap height is obtained by adding the depth of the plate to this value. By positioning the cursor at two different locations (x1 , y 1) and (x2 , y2) on the linear portion of the slope on the left side of the heap, the angle of repose could be determined using the formula

The same procedure is repeated on the right side of the heap. The average gives the angle of repose. The heap profile also could be obtained by marking various points on the heap outline in the image. To expedite this repetitive task a program was developed in visual basic with a user interface. A typical computer screen layout displaying the user interface is given in Figure 4. The first eight points are specific to do calculations as explained in Table 2. Point 9 to point 100 can be used to trace the heap profile, if needed.
The development of the software has considerably reduced the time taken for processing each image of the heap profile. Since the pixel to millimeter conversion and calculation of the repose angle would be performed by the program itself, it reduces the effort on the part of the user. The user has to define the first set of eight points to get the above results. Since flexibility is given to move and reorient any point, greater accuracy can be achieved in positioning a marker point exactly at a particular location. For getting the heap profile, the user selects discrete points on the heap outline starting with the left edge of the heap and completing with the right edge. The output is written to a data file for later retrieval or further processing. The repose angle is extracted from the slopes of the heap on the left and right sides. Each experiment is repeated three times and hence the repose angle for a given set of initial conditions is obtained by taking the average of six values.
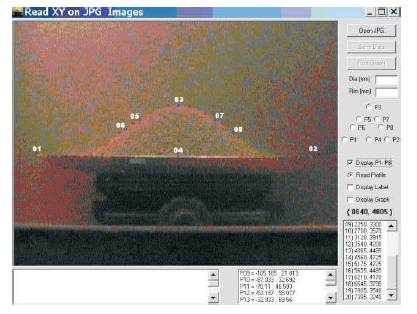
Figure 4. Layout of the Screen

Table 2. User Specified Points
Experiments were conducted by varying one parameter at a time, the parameters being granular mass flow rate, height of fall and water temperature as explained in section 4.0 to obtain different values for Re, Fr and Ar respectively. This is carried out with the view to investigate the influence of these numbers on the repose angle.
The dependence of repose angle on Reynolds number is represented in Figure 5.
The velocity of impact of the spheres on the heap increases with Re. Higher impact velocity leads to sliding of spheres down the slope and hence a decrease in angle of repose. It is seen that the angle of repose decreases with increase in Reynolds number and it exhibits a power law dependence on Re.
Froude number was varied by varying the height of fall of the spheres. The dependence of repose angle on Froude number is represented in Figure 6. The power law coefficient is positive here because height of fall is inversely related to both Froude number and angle of repose.
Experiments were conducted by var ying water temperature and hence its viscosity to assess the dependence of repose angle on Archimedes number which is represented in Figure 7. Viscosity of water decreases with temperature. Lesser viscosity of the fluid leads to better heaping. Repose angle shows an increasing trend with increase in Archimedes number.
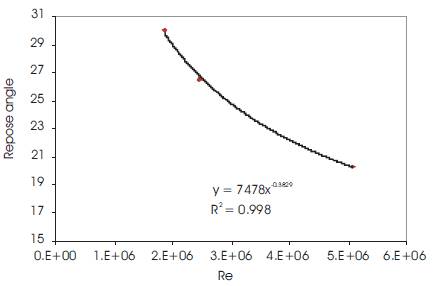
Figure 5. Dependence of on Reynolds number
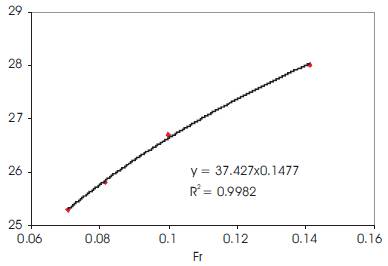
Figure 6. Repose Angle vs Froude Number
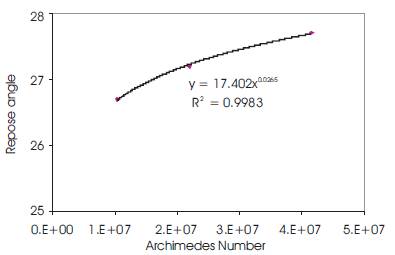
Figure 7. Dependence of on Archimedes
Multiple regression analysis has been carried out on the experimental data to establish the dependence of angle of repose on Re, Fr and Ar simultaneously. The measured angle of repose varied from 25o to 31o for the imposed initial conditions of the experiments. The correlation obtained from the analysis is
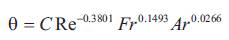
Where the constant of proportionality C=6624. The error involved in the estimation of constant of proportionality is 1.1%.
The range of the numbers calculated from the experimental conditions and used in obtaining this correlation is tabulated below in Table 3.
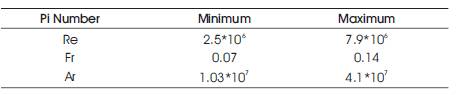
Table 3. Range of Pi numbers
The regression coefficient is 0.99 which indicates that the correlation between the data is very good.
Dimensional analysis has been performed to identify the dimensionless groups influencing the heaping behaviour of spherical particles falling inside quiescent liquid. Experiments are conducted by dropping lead spheres in water to mimic the heaping behaviour of UO2 in sodium. The measured angle of repose varies from 25o to 310 and is in close agreement with the values reported in open literature. The dependence of repose angle on dimensionless numbers Re, Fr and Ar is brought out in this study. From the experimental data, an empirical correlation is developed between the dimensionless numbers which could be used in the analysis of core debris heap formation in reactor accident simulation studies.
The authors extend their thanks to Dr. P. Chellapandi, Director, NSEG and Shri. B.K. Nashine, Head, SED for their support and motivation.
d diameter of particle
g acceleration due to gravity
h height of fall
k neutron multiplication factor
m mass of debris
t time
v velocity of par
H height of heap
R radius of heap
Greek symbols
Δρ density difference between particle and the fluid
µ viscosity of the fluid
ρ density of the particle
ρt density of the fluid
Subscripts
eff effective
f fluid
m model
p prototype
s solid particle
Pi numbers
θ Repose angle
Ar Archimedes number
Fr Froude number
Re Reynoldsnumber