A scenery can be visualized as an original from the short distance by using the well-focused imaging systems. Whereas, in the long distance, there are difficulties during the imaging process such as atmospheric turbulence, unfocused lenses of automatic imaging systems etc. As known, atmospheric turbulence between the imaging system and the scenery nonlinearly change from time to time and place to place via the hot, the warm or the cold weather and its degradation parameters can not be controlled during the imaging process. This type degradation known as blurring is the result of the spreading of the pixels to the neighborhood pixels. Because of the atmospheric turbulence during the imaging, they can not contain enough detail information. As a result of this, the researchers can not obtain correct results using these images. Therefore, the remote sensing images must be handled by using the image processing techniques before they can not be presented to the researchers. Generally, blurred images are restored in two categories [2-5]. With humankind's recent interest in global climatology and the impact that we have made on our environment, there is a pressing need for fast, accurate measurements of key global parameters such as ocean wind speed, ocean height, and land and ice characteristics. Some of the land and ice characteristics that are of interest include snow-cover classification, plant and soil moisture content, vegetation classification, and polar ice-extent mapping. While the definition of remote sensing describes a very wide array of technologies and types of research, all remote sensing technologies are based on certain common concepts, and all remote sensing systems consist of the same basic components. These four basic components of a remote sensing system include a target, an energy source, a transmission path, and a sensor (Figure 1).

The image is then interpreted in order to extract information about the target. This interpretation can be done visually or electronically with the aid of computers and image processing software. Weather satellite imaging of the Earth is a familiar example of a remote sensing system. Most forms of astronomy are examples of remote sensing, since the targets under investigation are such vast distances from Earth that physical contact is impossible. Astronomers therefore must collect and analyze the energy given off by these objects in space by using telescopes and other sensing devices. This information is recorded and used to draw conclusions about space and our universe. In order to take advantage of and make good use of remote sensing data, we must be able to extract meaningful information from the imagery. Image enhancement and analysis of remote sensing imagery involves the identification and/or measurement of various targets in an image in order to extract useful information about them. Targets in remote sensing images may be any feature or object which can be observed in an image. Targets may be a point, line, or area feature. This means that they can have any form, from a bus in a parking lot or plane on a runway, to a bridge or roadway, to a large expanse of water or a field [6-7].

Figure 1. Basics of Remote Sensing.

Contrast of outdoor images acquired under adverse weather conditions, especially foggy weather, is altered by scattering of daylight by atmospheric particles .As a consequence, different methods have been designed to restore the contrast of the images. However, there is lack of methodology to assess the performances of the methods to rate them [8-10]. Remote Sensing (RS) refers to the science of identification of earth surface features and estimation of their geo-biophysical properties using electromagnetic radiation as a medium of interaction. Spectral, spatial, temporal and polarization signatures are major characteristics of the sensor/target, which facilitate target discrimination [11]. Maps of the lunar neutron albedo will be determined from the orbiting Lunar Exploration Neutron Detector (LEND) onboard the Lunar Reconnaissance Orbiter (LRO) spacecraft. Slated for an October 2008 launch, on a nominal yearlong mission, LEND will characterize the surface distributions of hydrogen and other cold trapped volatiles relevant to future exploration missions. As part of the LEND mission planning activities the instrument team is investigating methods for enhancing the accuracy and quality of maps. Jansson Van-Cittert's (JVC) image restoration transform is cited in the literature in applications relevant to planetary remote sensing deconvolution applications [12]. Overall, the application of image restoration to MODIS imagery was capable of recovering some spatial information and improving the information content of MODIS imagery. Although the variations arising from such differing spatial resolutions were still present after restoration, the algorithm was capable of reducing the gaps between results obtained from TM and MODIS imagery in most cases, with considerable enough gains to generate sets of measurements significantly different than those computed from original MODIS imagery. As expected, measurements of shape such as perimeter and shape indexes were the ones most sensitive to scale and spatial resolution changes, thus exhibiting the smallest improvements[13]. The image restoration plays an important role in remote sensing, an astronomical image anlysis and applications. One common method for recovery of blurred image is using LSE (Least Squares Error) methods[14].

Image Restoration, like image enhancement, aims to improve the pictorial information in an image. Unlike image enhancement, it is assumed in image restoration that some information about the corrupting process is known, in the form of a degradation model. The degradation model allows one to mathematically obtain an operation that can best "undo" the degradation in some sense, and thus restore the original, uncorrupted image. Such optimal operation is called the restoration filter. It is common to assume an additive model i.e. corrupted image is affected with some noise or degradation. The degradation is an unwanted distortion introduced by the imaging system. The noise represents a spurious component that is added to the image [15-17].

There is a technique known as Wiener filtering that is used in image restoration. This technique assumes that if noise is present in the system, then it is considered to be additive white Gaussian noise (AWGN). Wiener filtering normally requires a priori knowledge of the power spectra of the noise and the original image. What if the spectral density functions of the image and noise are unknown? In this case, we use a parametric version of the Wiener filter. A simplified equation of the Wiener filter R(u) is given below:

(1)

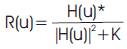
The inverse filter of a blurred image is a high pass filter. The parameter K of the Wiener filter is related to the low frequency aspect of the Wiener filter. The Wiener filter behaves as a as a band pass filter, where the high pass filter is due to the inverse filter and the low pass filter to the parameter K. When K=0, the Wiener filter becomes the inverse filter. In image restoration the goal is to recover an image that has been corrupted or degraded. The more information we have of the degradation process, the better off we are. This is known as a priori knowledge. There are several techniques in image restoration, some use frequency domain concepts, others attempt to model the degradation and apply the inverse process. The modeling approach requires determining a criterion of "goodness" that will yield an "optimal" solution [15].

Let f be the original image, h the blurring kernel, and g the blurred image. The idea in inverse filtering is to recover the original image from the blurred image. From the convolution theorem, the DFT of the blurred image is the product of the DFT of the original image and the DFT of the blurring kernel. Thus, dividing the DFT of the blurred image by the DFT of the kernel, one can recover the original image. Then the inverse frequency filter, R(u), to be applied is 1/H(u). We have assumed no noise is present in the system. Observe the difficulties we encounter when H(u) is very small or equal to zero.

(2)

(3)

(4)

(5)

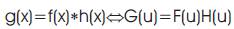
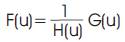
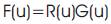
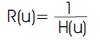
The authors have implemented the enhancement techniques on PIV 2.4 GHz using MATLAB 7.5. The enhanced images after subjecting the original images to contrast enhancement and histogram equalization are compared along with the CNR, PSNR and RMS error [18- 19].

Some of the remotely sensed images from database are shown in Figure 2. For K=143.39, Weiner filter and inverse filter produced the resulting image shown in Figure 3. Here PSNR considered of noise is 05 dB. It provided calculated PSNR of 4.87 and RMS error of 145.41.For K=80.63, Weiner filter and inverse filter produced the resulting image shown in Figure 4. Here PSNR considered of noise is 10 dB. It provided calculated PSNR of 9.56 and RMS error of 84.77.For K=25.5, Weiner filter and inverse filter produced the resulting image shown in Figure 5. Here PSNR considered of noise is 20 dB. It provided calculated PSNR of 17.08 and RMS error of 35.65.

Figure 2. Remotely Sensed Images (a-e), where (a) is particularly image of moon sent by CHANDRAYAN

Figure 3. Result of PSNR = 5 dB

Figure 4. Result of PSNR = 10 dB

Figure 5. Result of PSNR = 20 dB

Finally increasing the PSNR of noise and for or K=25.5, Weiner filter and inverse filter produced the resulting image shown in Figure 6. Here PSNR considered of noise is 35 dB. It provided calculated PSNR of 20.04 and RMS error of 25.37. The above procedure repeated for a number of images. The detailed comparison of all the features viz. CNR, PSNR, RMS error etc. has been compared for moon image in Table 1 and it has been plotted in Chart 1. It is clear that when PSNR is increased i.e. noise content added is reduced then CNR is increasing which indicates that there is increase in contrast value that will make the image better for researcher. Similarly, with the increase in SNR input, RMS error is decreasing although calculates PSNR after restoration process is increasing slowly.

Figure 6. Result of PSNR = 35 dB

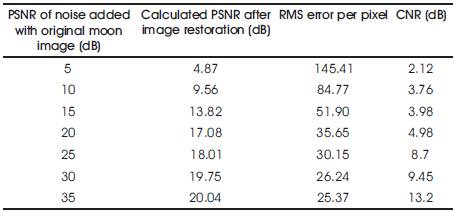
Table 1. An assessment of Filters in terms of PSNR, CNR, and RMS error

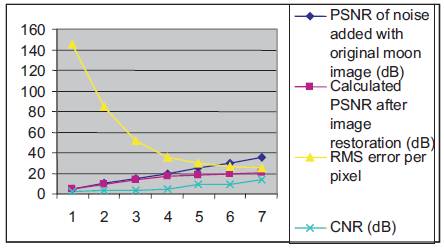
Chart 1. A plot of CNR, PSNR and RMS error with increase in PSNR input

Most remote sensing applications use restoration technique as a post processing stage for feature extraction. Remote sensing images can be corrupted with point noise. Image restoration using Weiner filtering in remote sensing has been assessed. So, the present analysis can make the feature extraction process in remote sensing applications much easier and efficient for space scientists. This paper presents restoration technique that performs both visually and quantitatively since there is significant increase in contrast and decrease in RMS error. If deconvolution does not work, or performs poorly, one should use the Wiener filter. In fact, if there is no noise, then the Wiener filter reduces to the inverse filter, showing that the latter is indeed the optimal linear MSE (Minimum Square Error) filter.