The cutting stock problem is the cutting of pieces of various sizes and shapes from a standard length of a given material (stock sheet), while minimizing the wastage of the stock material. This problem arises in many situations in industrial production planning . Some of them are cutting steel or glass sheets into required stock sizes, cutting wooden plates to make furniture, cutting paper board to make boxes, placing advertisements on the pages of newspapers, etc. Also, the unrestricted form of this problem arises in the textile industry. In the paper manufacturing industry, 'jumbo' reels of paper are to be cut into narrower 'custom' reels according to specifications. In aircraft manufacturing industry, very expensive sheet metal stocks can be wasted in inefficient layouts.

In this paper, we consider the one - dimensional cutting stock problem which may be defined as the cutting of stock material of standard lengths into small pieces of required lengths in order to satisfy a given demand. Here, an attempt is made to reduce the wastage or 'trim loss' occurred during the cutting process. However, in many situations it may not be possible to make any use of the remaining pieces and thus they are wasted. Therefore, in this paper, we look for a procedure which tries to minimize the number of stock lengths which satisfies the demand rather than minimizing the trim loss because both problems are equivalent. In this study, we confine our attention to the case where there exists only one standard length of a given stock material.

Given a sheet of standard length, there can be many ways of cutting it according to the specifications of required cut pieces. Each such way is called a cutting pattern. The number of stock sheets containing each cutting pattern should be integer in order to satisfy the demand. This gives rise to a very complicated combinatorial problem as the number of different cutting patterns that could be constructed from a given stock sheet could be enormous in a large problem. Attempts have been made to solve this problem by relaxing integrality conditions and obtaining a linear programming formulation [Gilmore and Gomory,1961]. This linear programme could be solved by developing a special column generation technique based on Dantzig- Wolfe decomposition principle [Bazaraa, Jarvis and Sherali, 1990]. Another formulation assumed that the 'trim loss' is not useless but has a value for further demands arising in later planning periods[Dyckhoff, 1981] . Again a linear programming method was used for solution. A fixed charge is associated with a cutting pattern in certain other models [Haessler, 1975]. Here, the idea was to limit the number of pattern changes while reducing the 'trim loss'. A heuristic procedure has been proposed here. A local search algorithm using linear programming techniques has been proposed in another approach (Umetani et.al., 2003). In this approach, an initial set of patterns was constructed using the first fit heuristic known for the bin packing problem. The algorithm then repeats replacing the current set of patterns with a better set in its neighbourhood until no better set is found in the neighbourhood. A branch and bound method which gives exact solutions has also been proposed (Scheithauer and Terno, 1995). Unfortunately, this method could find optimal solutions only when the problem size is small.

But, the most common approach for solving this problem appears to be linear programming relaxations even though there are considerable differences among various models. These models suffer from drawbacks common to such formulations. When integer programming models are approximated to linear programming formulations, the quality of solutions cannot be guaranteed always; they depend very much on the problem data. Another disadvantage is that, large amount of computation have to be carried out unnecessarily to arrive at an acceptable solution.

We disuss the method of obtaining integer solutions in Section 2 of this paper. In Section 3, we present the mathematical model. Computational procedure is discussed and the algorithm is presented in Section 4. We describe the method of obtaining lower and upper bounds to determine the quality of solutions in Section 5. In Section 6, we present the computational experience related to data from a real industrial application. Concluding remarks are given in Section 7.

We propose an algorithm which generates feasible solutions by forming linear combinations of set of linearly independent vectors in a basis from a vector space [hadley, 1962]. Each vector in the basis represents a cutting pattern. The basis is updated at every iteration leading to a new solution. We consider a space of cutting patterns of dimension m representing different sizes of cut pieces required for an order. Any order is represented by a vector of dimension m which belongs to the vector space of cutting patterns. As any vector in the space can be represented by a linear combination of basis vectors, any demand vector can be satisfied by considering only m vectors representing cutting patterns. Hence a basis contains m vectors representing m cutting patterns which satisfies the demand. In other words, each basis represents a combination of cutting patterns leading to a feasible solution.

An initial feasible solution is obtained from a linear combination of vectors in which each vector representing a cutting pattern made of cut pieces of only one size. This solution is gradually improved by introducing new vectors (cutting patterns) into the basis which leads to the gradual reduction of wastage in cutting patterns. Usually, the number of different sizes to be cut from a standard length is also gradually increased by this process. However, the algorithm proceeds in a way such that the number of different sizes to be cut from a piece is as small as possible. This is preferable in practical situations as it will reduce the number of pattern changes to be carried out too.

In the proposed algorithm, we maintain the condition of integrality at every iteration by two means. First, it is ensured that each cutting pattern will consist of an integer number of cut pieces of different lengths, apart from the wastage if any, in the cutting pattern. Then, we solve the set of constraints containing the demand for each cut piece, so that the number of stock lengths required from each cutting pattern is always integer. Hence, the solution obtained at each iteration is integer. Therefore, if necessary, making use of any intermediate solution for implementation is quite possible. Also, iterations can be terminated at any desirable point, giving rise to a feasible solution. However, any intermediate infeasible solution will not be considered.

Let L be the standard length of a stock sheet. Since we consider the one dimensional problem, we assume that the width of every piece to be cut is uniform. It is assumed that an order has been placed for the supply of bi pieces ( cut pieces) of length li where i = 1,2, …,m.

Now the problem is to cut the standard sheets or rolls in such a way that the order is completely satisfied while the wastage is minimized. We assume here that the remaining cut pieces are of no value to the manufacturer. Therefore, our objective is to minimize the number of stock sheets of standard length required to satisfy the given demand.

It is possible to cut a sheet of standard length (stock sheet) into cut pieces of various lengths in many different ways, depending on the lengths of cut pieces required. Each such way of cutting is called a cutting pattern.

Let us denote the j^th cutting pattern by a_j . The i^th component of a_j is denoted by a_ij which indicates the number of cut pieces of length l i in the j^th cutting pattern.

It can be observed that the vector a_j represents a cutting pattern if and only if

and each a_ij is a non-negative integer. The number of all possible cutting patterns (n) is finite but can be very large, because various combinations of cut pieces of different sizes can be included in a particular cutting pattern. Let xj be the number of stock lengths to be cut according to the jth pattern. We wish to minimize the total number of stock lengths required to satisfy the demand.

Then, the problem becomes

 

 

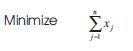
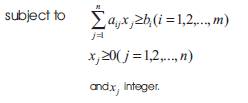
This is an extremely difficult integer programming problem. The difficulty is mainly due to the existence of very large number of possible cutting patterns. Therefore, it is not computationally feasible to enumerate each cutting pattern beforehand. The other difficulty is, due to the requirement that the number of stock lengths to be cut according to each pattern has to be integer. Therefore, the common approach to solve this problem has been to relax integrality conditions so that a linear programming formulation is possible. However, this approach will lead to solutions which may not be satisfactory in all cases.

In our proposed algorithm, we make use of only m cutting patterns at any given time in order to satisfy the requirements, since any demand vector can be generated using m linearly independent vectors (cutting patterns).

In this section we present the steps of the proposed algorithm and a discussion on the steps involved.

4.1 Algorithm

Step (0) : constructing an initial solution

Construct an initial basis consisting of m linearly independent vectors (cutting patterns)

a₁,a₂,....,a_j,....,a_m

The vector a_j is defined as a_j = (a_1j ,a_{2 j} ,....,a_ij ,...,a_mj )

where

 

Here, a_ij is the number of cut pieces of length l_i in the j^_th cutting pattern

and k = the maximum number of cut pieces of length lj that can be cut from a stock sheet of length

l. b_j = demand for cut pieces of length l_j .

Compute the minimum number of stock sheets ( xj ) required from each cutting pattern to fill the demand. Record the amount of wastage for each cutting pattern.

Step (1) : constructing an improved solution (by introducing cut pieces of different lengths to cutting patterns ).

Select the cutting pattern with the highest wastage in the current solution. If this wastage is < l1 (ie. length of the smallest cut piece) goto step (2). Otherwise, reduce this wastage by introducing cut pieces of a different length to the cutting pattern if possible. If the number of cut pieces that could be introduced into the cutting pattern exceeds the amount required to satisfy demand , introduce just enough number of cut pieces to satisfy demand. Perform this operation for all cutting patterns with wastages wherever possible by arranging wastages in descending order.

Step (2) : constructing an improved solution (by redistributing the number of cut pieces within cutting patterns)

For each cutting pattern with a wastage > 0, if possible, reduce wastage by redistributing number of cut pieces of different lengths within individual cutting patterns. This is done by reducing the number of cut pieces of a particular length in the pattern and introducing an additional piece of a different length to the pattern. Repeat this step until anymore cutting patterns could not be further adjusted.

4.2. Construction of the initial solution

The initial feasible solution to the problem is constructed by generating m linearly independent vectors (cutting patterns) each having m components. We construct a set of m linearly independent vectors

a₁,a₂,....,a_j,....,a_m such that a_j = (a_1j ,a_{2 j} ,....,a_ij ,...,a_mj )

 

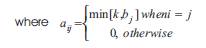
Here the non-zero entry in each vector is equal to the integer value (k) which indicates the maximum number of pieces of length l_j that could be cut from a stock sheet of length L. ie. =a_jj k. However, if the demand b_j for pieces of length l_j is less than this number, k will take the value of the demand. This is implemented by the Step (0) of the algorithm.

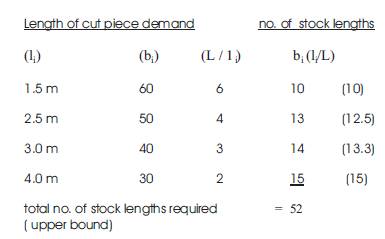
As an example, consider a situation in which stock length L = 10 m where four cutting lengths are required as l1 = 1.5, l2 = 2.5, l3 = 3.0, l4 =4.0. Let us assume that the amounts required from each length are

b1 = 60, b2 = 50, b3 = 40 and b4 = 30 respectively.

Then, the initial basis will consist of the following vectors

 

In order to fulfil the demand , a linear combination of these vectors should satisfy the inequality

 

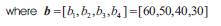
which leads to the inequalities

 

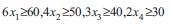
The minimum integer values xj which satisfies these inequalities are given by,

 

 

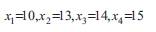
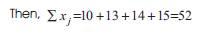
According to this solution, the number of standard rolls to be cut to satisfy the demand is 52. However, ∑b_il_i=455 gives the total length of the requirements. Since each standard roll is of length 10 m , the minimum possible number of rolls required is 46. This gives a lower bound for the optimal solution.

4.3 Improving solutions by reducing wastages

When a cutting pattern is generated, the remaining length of the cutting pattern from the stock sheets lead to wastage. The number of stock sheets to be utilized for each pattern in order to satisfy the demand also leads to wastage as the demand may be over supplied. This is because of the requirement that x_j values should be integer. We attempt to reduce both these types of wastages using the proposed algorithm.

This wastage could be reduced in two stages:

Introduce cut pieces of a different size to the cutting pattern if possible.

Rearrange the number of cut pieces of different lengths within a cutting pattern to make use of more length of the stock sheet.

Let us consider the first stage of reducing wastages in cutting a_j patterns. For each vector (cutting pattern) in the current solution, the amount of wastage (wj) is recorded where 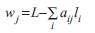Then, the amount of wastage in the initial solution of the example is given by

 

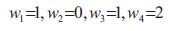
Now, we try to obtain a solution which reduces wastage in cutting patterns. In order to do this, the vector (cutting patterns) which incurs the highest wastage in the current solution is selected and we try to improve it by reducing its wastage. Here, the vector corresponding to the highest wastage is

 

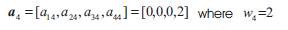
The wastage in this cutting pattern may be reduced by increasing the number of pieces to be cut from a stock piece of standard length. This is implemented using the Step (1) of the algorithm.

This cutting pattern a₄ could be improved by introducing one piece of length l1 = 1.5 m to the cutting pattern. This is possible since 1.5 m is less than the wastage w₄=2 in this cutting pattern. Hence, the new cutting pattern which replaces the above cutting pattern is given by a₄= [ 1, 0 , 0, 2]. As a result, the wastage (w4) in the new cutting pattern a₄ is reduced to 0.5 m.

Now the new solution contains the vectors,

 

Then, the corresponding wastages in cutting patterns are given by

 

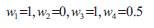
At this stage, the wastages of all cutting patterns in the current solution is less than the smallest possible length of a cut piece (1.5 m). Hence, further reduction of wastage by adding cut pieces to individual cutting patterns is not possible.

The set of constraints corresponding to the current solution is given by

 

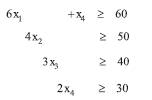
These constraints will be satisfied by

 

However, it may still be possible to reduce the wastages in individual cutting patterns by redistributing the number of cut pieces within cutting patterns. This possibility is explored next. It is performed by the Step (2) of the algorithm.

We consider each cutting pattern in the current solution with a wastage (> 0) in turn and try to redistribute the number of cut pieces of different lengths within cut patterns so that the wastage is reduced.

The cutting pattern a₁ has a wastage w1 = 1 and this could be redistributed so that [6, 0, 0, 0] becomes [ 5, 1, 0, 0] and as a result wastage will become zero (ie.w1 = 0).

Now, the set of constraints become

 

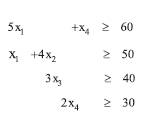
These are satisfied by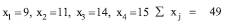

Next, we observe that vector a₃ with wastage w₃ = 1 could  also be adjusted so that wastage is reduced.

Then =[0,0,3, 0] becomes [0, 0, 2, 1] and the wastage w₃ becomes zero (ie.w₃ = 0).

Now the set of constriant becomes

 

 

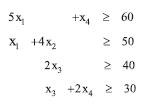
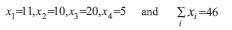
No more adjustments are possible, as we have reached the lower bound for the optimal solutions. Hence, the current solution leads to an optimal set of cutting patterns satisfying the demand.

In order to assess the quality of solutions, it is necessary to construct a suitable lower bounds and upper bounds for the optimal solution. One way to obtain a lower bound is to assume that it is possible to get each cut piece from a continuous roll of stock length. In the example considered, the total length of the requirements is given by ∑b_il_i=455. As the length of a stock sheet (L) is 10 m , the minimum number of stock sheets necessary to satisfy the demand will be 46. This gives a lower bound for the optimal solution. In the example, the solution we obtained also requires 46 stock sheets and thus we can see that the optimal solution has been reached in this case.

The following criterion can be used to obtain an upper bound on the optimal solution. For each type of cut piece with a specific length, we determine the number of cut pieces that could be obtained from a single stock length by dividing stock length (L) by the length of a cut piece (l_i).The result is truncated to obtain an integer value. Then the number of stock lengths needed to satisfy the demand for that particular type of cut piece is determined asuming that a particular stock length is cut using only a single type of cut piece. This process is continued for cut pieces of all sizes. The sum of stock lengths required to satisfy the demand for each type of cut piece will give an upper bound.

For the above example, the upper bound could be computed as follows.

 

We have solved 39 test instances taken from a real application in a chemical fibre company in Japan provided by Umetani (2003). In these problems number of order lengths (m) vary between 6 and 29. Lengths of stock sheets were 9080 and 5180. Demands for cutpieces (b_i) range from 2 to 264 while the lengths of cutpieces (l_i) vary between 500 and 2000. The results are given below.

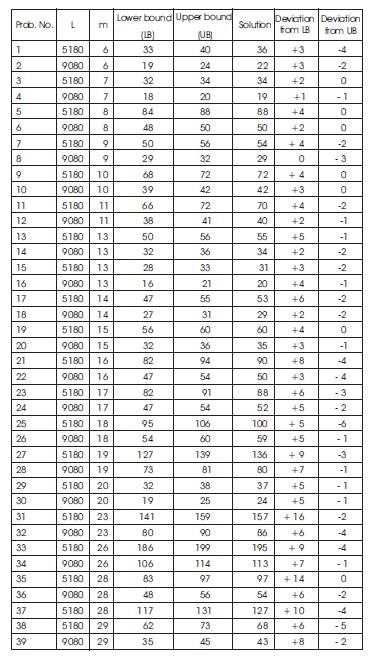
Table : Test problem characteristics and solutions

According to the above results, it can be seen that in most of the problems we have reached optimal or near optimal solutions.

We have presented a fast heuristic algorithm to solve the one dimensional cutting stock problem. Due to the limited number of cutting patterns considered in each iteration, the amount of computation needed to reach an acceptable solution is very much smaller compared to that of conventional methods. Besides, it has the advantage of attacking the original problem as it is, to get integer solutions during each iteration. One of the significant feature of the algorithm is that the number of cutting patterns involved in the solution is always less than or equal to the number of different types of cut pieces (m) required. According to the computational results, it can be seen that the solutions obtained are extremely good.